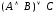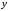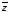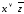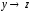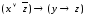2.5. Дизъюнктивные и конъюнктивные нормальные формы булевых функций

Определение 1. Конъюнктивным одночленом (элементарной конъюнкцией) от переменных 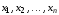называется конъюнкция этих переменных или их отрицаний.

Например, 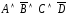– элементарная конъюнкция.

Определение 2. Дизъюнктивным одночленом (элементарной дизъюнкцией) от переменных 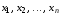называется дизъюнкция этих переменных или их отрицаний.

Например, 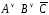– элементарнаядизъюнкция.

Определение 3. Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных конъюнктивных одночленов, называется дизъюнктивной нормальной формой (ДНФ) данной формулы.

Например, 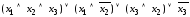– ДНФ.

Определение 4. Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных дизъюнктивных одночленов, называется конъюнктивной нормальной формой (КНФ) данной формулы.

Например, 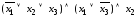– КНФ.

Для каждой формулы алгебры высказываний можно найти множество дизъюнктивных и конъюнктивных нормальных форм.

Алгоритм построения нормальных форм

1. С помощью равносильностей алгебры логики заменить все имеющиеся в формуле операции основными: конъюнкцией, дизъюнкцией, отрицанием:

;

;

.

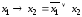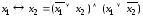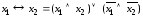2. Заменить знак отрицания, относящийся к выражениям типа 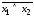или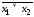, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

; .

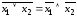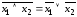3. Избавиться от знаков двойного отрицания.

4. Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

2.6. Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы

Любая булева функция может иметь много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).

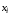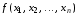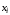Определение 1. Совершенная дизъюнктивная нормальная форма (СДНФ) – это ДНФ, в которой в каждый конъюнктивный одночлен каждая переменная из наборавходит ровно один раз, причем входит либо сама, либо ее отрицание.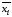

Конструктивно СДНФ для каждой формулы алгебры высказываний, приведенной к ДНФ, можно определить следующим образом:

Определение 2. Совершенной дизъюнктивной нормальной формой (СДНФ) формулы алгебры высказываний называется ее ДНФ, обладающая следующими свойствами:

1. ДНФ не содержит двух одинаковых конъюнкций;

2. ни одна конъюнкция не содержит одновременно двух одинаковых переменных;

3. ни одна конъюнкция не содержит одновременно некоторую переменную и ее отрицание;

4. каждая конъюнкция содержит либо переменную 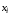, либо ее отрицание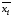для всех переменных, входящих в формулу.

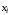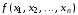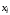Определение 3. Совершенная конъюнктивная нормальная форма (СКНФ) – это КНФ, в которой в каждый дизъюнктивный одночлен каждая переменная из наборавходит ровно один раз, причем входит либо сама, либо ее отрицание.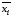

Конструктивно СКНФ для каждой формулы алгебры высказываний, приведенной к КНФ, можно определить следующим образом.

Определение 4. Совершенной конъюнктивной нормальной формой (СКНФ) данной формулы алгебры высказываний называется такая ее КНФ, которая удовлетворяет следующим свойствам.

1. КНФ не содержит двух одинаковых дизъюнкций.

2. Ни одна конъюнкция не содержит одновременно двух одинаковых переменных.

3. Ни одна из дизъюнкций не содержит одновременно некоторую переменную и ее отрицание.

4. Каждая дизъюнкция СКНФ содержит либо переменную 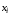, либо ее отрицание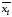для всех переменных, входящих в формулу.

Теорема 1. Каждая булева функция от переменных, не являющаяся тождественно ложной, может быть представлена в СДНФ, и притом единственным образом.

Способы нахождения СДНФ

1-й способ – с помощью равносильных преобразований:

• получаем одну из ДНФ;

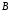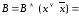
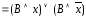• если в полученной ДНФ входящая в нее элементарная конъюнкция не содержит переменную, то используем равносильностьи получаем две элементарных конъюнкции;

• если в ДНФ входят две элементарные конъюнкции, то лишнюю можно отбросить.

2-й способ – с помощью таблиц истинности:

• выделяем строки, где формула принимает значение 1;

• составляем дизъюнкцию конъюнкций при условии, что если переменная входит в конъюнкцию со значением 1, то записываем эту переменную, если со значением 0, то ее отрицание. Получаем СДНФ.

Теорема 2. Каждая булева функция от переменных, не являющаяся тождественно истинной, может быть представлена в СКНФ, и притом единственным образом.

Способы нахождения СКНФ

1-й способ – с помощью равносильных преобразований:

• получаем одну из КНФ;

• если в полученной КНФ входящая в нее элементарная дизъюнкция 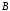не содержит переменную, то используем равносильность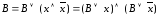и получаем две элементарных дизъюнкции;

• если в КНФ входят две элементарные дизъюнкции, то лишнюю можно отбросить.

2-й способ – с помощью таблиц истинности:

• выделяем строки, где формула принимает значение 0;

• составляем конъюнкцию дизъюнкций при условии, что если переменная входит в дизъюнкцию со значением 0, то записываем эту переменную, если со значением 1, то ее отрицание. Получаем СКНФ.

Пример 1. Постройте КНФ функции .

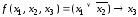Решение

Исключим связку «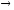» с помощью законов преобразования переменных:

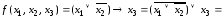
= /законы де Моргана и двойного отрицания/ =

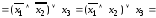/дистрибутивные законы/ =

.

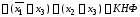Пример 2. Приведите к ДНФ формулу .

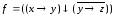Решение

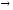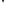Выразим логические операции ичерез,и:

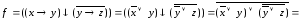
= /отнесем отрицание к переменным и сократим двойные отрицания/ =

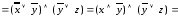
= /закон дистрибутивности/ .

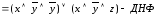Пример 3. Запишите формулу в ДНФ и СДНФ.

Решение

Используя законы логики, приведем данную формулу к виду, содержащему только дизъюнкции элементарных конъюнкций. Полученная формула и будет искомой ДНФ:

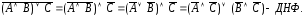
Для построения СДНФ составим таблицу истинности для данной формулы:

0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 0 0 0 1 1	0 1 0 1 0 1 1 1	1 0 1 0 1 0 0 0

Помечаем те строки таблицы, в которых формула (последний столбец) принимает значение 1. Для каждой такой строки выпишем формулу, истинную на наборе переменных 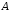,,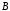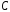данной строки:

строка 1: ;

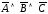строка 3: ;

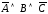строка 5: .

Дизъюнкция этих трех формул будет принимать значение 1 только на наборах переменных в строках 1, 3, 5, а следовательно, и будет искомой совершенной дизъюнктивной нормальной формой (СДНФ):

.

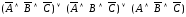Пример 4. Приведите формулу 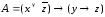к СКНФ двумя способами:

а) с помощью равносильных преобразований;

б) с помощью таблицы истинности.

Решение:

a)

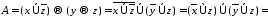
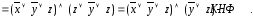
Преобразуем вторую элементарную дизъюнкцию:

.

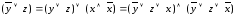Формула имеет вид:

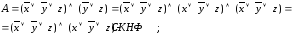
б) составим таблицу истинности для данной формулы:

1 1 1 1 0 0 0 0	1 1 0 0 1 1 0 0	1 0 1 0 1 0 1 0	0 1 0 1 0 1 0 1	1 1 1 1 0 1 0 1	1 0 1 1 1 0 1 1	1 0 1 1 1 0 1 1

Помечаем те строки таблицы, в которых формула (последний столбец) принимает значение 0. Для каждой такой строки выпишем формулу, истинную на наборе переменных ,,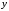данной строки:

строка 2: ;

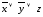строка 6: .

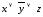Конъюнкция этих двух формул будет принимать значение 0 только на наборах переменных в строках 2 и 6, а следовательно, и будет искомой совершенной конъюнктивной нормальной формой (СКНФ):

.

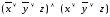Вопросы и задачи для самостоятельного решения

1. С помощью равносильных преобразований приведите к ДНФ формулы:

а) ;

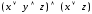б) ;

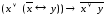в) .

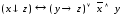2. С помощью равносильных преобразований приведите к КНФ формулы:

а) ;

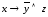б) ;

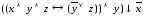в) .

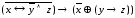3. С помощью второго дистрибутивного закона преобразуйте ДНФ в КНФ:

а) ;

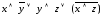б) .

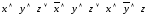4. Преобразуйте заданные ДНФ в СДНФ:

а) ;

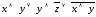б) ;

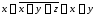в) .

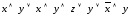5. Преобразуйте заданные КНФ в СКНФ:

а) ;

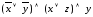б) ;

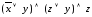в) .

6. Для заданных логических формул постройте СДНФ и СКНФ двумя способами: с помощью равносильных преобразований и с помощью таблицы истинности.

а) ;

б) ;

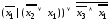^в)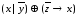.