
- •В.С. Васильева, с.В. Коровина, л.В. Марченко дискретная математика
- •Васильева, в.С.
- •Введение
- •1. Элементы теории множеств
- •1.1. Основные понятия теории множеств. Способы задания множеств
- •1.2. Операции над множествами
- •1.3. Диаграммы Эйлера – Венна
- •1.4. Свойства операций над множествами
- •1.5. Декартово произведение множеств
- •1.6. Бинарные отношения. Свойства бинарных отношений
- •1.7. Функция
- •2. Элементы математической логики
- •2.1. Математическая логика как наука
- •2.2. Высказывания. Логические операции и их основные свойства
- •Логические операции
- •Новые логические операции
- •2.3. Способы решения логических задач
- •2.4. Булевы функции. Свойства элементарных булевых функций
- •2.5. Дизъюнктивные и конъюнктивные нормальные формы булевых функций
- •2.6. Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
- •3. Элементы теории графов
- •3.1. Основные понятия теории графов
- •3.2. Способы задания графов
- •3.3. Связность графов
- •4. Элементы комбинаторики
- •4.1. Перестановки, размещения и их количество
- •4.2. Сочетания и их свойства
- •4.3. Выборки с повторением
- •5. Индивидуальные задания
- •Заключение
- •Библиографический список
- •Оглавление
3.2. Способы задания графов
В
подразд. 3.1 мы уже познакомились с двумя
способами описания графов: в
виде задания двух множеств вершин
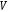 и ребер
и ребер и
графическим
способом.
и
графическим
способом.
Рассмотрим другие способы задания графов.
Матрица инцидентности
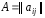 .
.
Пусть
дан граф
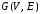 ,
где
,
где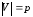 – количество вершин,
– количество вершин,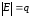 – количество ребер, тогда матрица
инцидентности имеет размер
– количество ребер, тогда матрица
инцидентности имеет размер .
.
Для неориентированного графа она имеет вид

Для орграфа

Замечание 1. Если граф без петель, то в матрице смежности по главной диагонали стоят нули.
Пример 1. Составьте матрицы инцидентности для следующих графов (рис. 26, а, б).
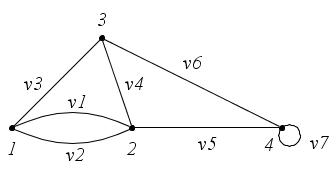
а
б
Рис. 26
Решение:
а)
 ;
б)
;
б) .
.
В
каждом столбце матрицы инцидентности
неориентированного или ориентированного
графа только два элемента отличны от
нуля (или один, если ребро является
петлей). Для матрицы инцидентности
ориентированного графа либо столбец
содержит один элемент, равный 1, либо
один элемент, равный
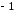 ,
либо столбец нулевой.
,
либо столбец нулевой.
Отношение инцидентности можно еще задать списком ребер графа. Каждая строка этого списка соответствует ребру, в котором записаны номера вершин, инцидентных ему.
2.
Матрица смежности
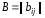 .
.
Пусть
дан граф
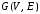 ,
где
,
где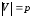 – количество вершин, тогда матрица
смежности отражает смежность вершин и
имеет размер
– количество вершин, тогда матрица
смежности отражает смежность вершин и
имеет размер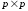 .
.
Для неориентированного графа она имеет вид

Для орграфа
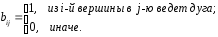
Для
неориентированного мультиграфа значение
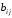 равно количеству ребер, инцидентныхi-й
и j-й
вершинам, для ориентированного графа
этот элемент матрицы смежности равен
количеству ребер с началом в i-й
вершине и концом в j-й.
Таким образом, матрица смежности
неориентированного графа симметрична,
а ориентированного – не обязательно
симметрична.
равно количеству ребер, инцидентныхi-й
и j-й
вершинам, для ориентированного графа
этот элемент матрицы смежности равен
количеству ребер с началом в i-й
вершине и концом в j-й.
Таким образом, матрица смежности
неориентированного графа симметрична,
а ориентированного – не обязательно
симметрична.
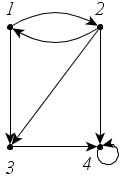
Пример 2. Найдите матрицы смежности для графов (рис. 27, а, б).
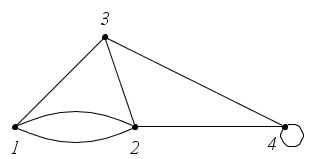
б
а
Рис. 27
Решение
а)
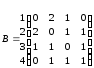 ;
б)
;
б)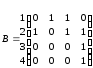 .
.
Замечание 2. Для неориентированного графа матрица смежности симметричная.
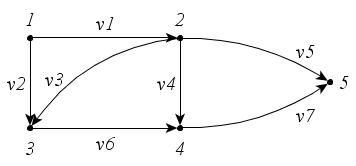
Пример
3.
Нарисуйте граф
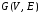 c
множеством вершин
c
множеством вершин
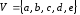 и множеством ребер
и множеством ребер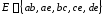 .
Найдите его матрицу смежности.
.
Найдите его матрицу смежности.
Решение
Изображение
графа
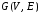 представлено на рис. 28.
представлено на рис. 28.
Так
как у графа пять вершин, то матрица
смежности будет
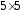 :
:
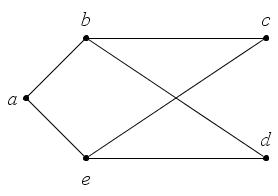
Рис. 28


Вопросы и задачи для самостоятельного решения
1. Перечислите способы представления графов. Дайте понятия матриц смежности и инцидентности.
2. Постройте граф по данной матрице смежности:

3. Для следующих графов найдите матрицы инцидентности и смежности (рис. 29, a, б):

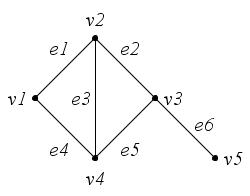
а
б
Рис. 29
Пронумеруйте вершины и ребра орграфов (рис. 30, а, б). Найдите для них матрицы инцидентности и смежности.
Можно ли нарисовать, не отрывая карандаша от бумаги и не проходя ни по одному их отрезков дважды, «домики с крышами» (рис. 31, а, б, в, г, д)?

а
б
Рис. 30
б
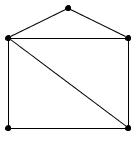
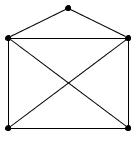
а
в
д
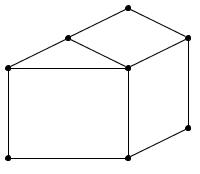
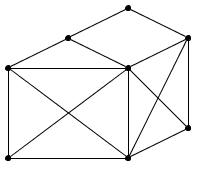
г
Рис. 31
3.3. Связность графов
Определение
1.
Граф (орграф)
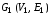 называютподграфом
графа (орграфа)
называютподграфом
графа (орграфа)
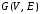 ,
если
,
если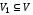 и
и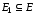 .
.
Будем
использовать обозначение
 ,
аналогичное обозначению включения для
множеств.
,
аналогичное обозначению включения для
множеств.
Определение
2. Если
хотя бы одно из указанных двух включений
в определении 1 строгое, то
 называютсобственным
подграфом
графа.
называютсобственным
подграфом
графа.
Например, графы на рис. 32 являются подграфами графа на рис. 33.
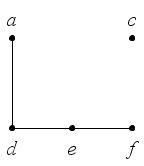
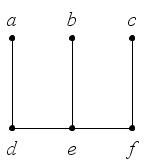
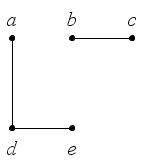
Рис. 32
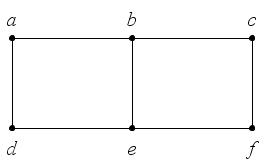
Рис. 33
Определение
3. Подграф
 называютмаксимальным
подграфом,
если он не является собственным подграфом
никакого другого подграфа
называютмаксимальным
подграфом,
если он не является собственным подграфом
никакого другого подграфа
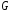 .
.
Например,
на
рис. 34 графы
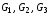 – максимальные подграфы графа
– максимальные подграфы графа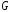 ,
причем они также являются собственными
подграфами.
,
причем они также являются собственными
подграфами.
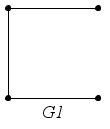
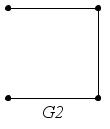
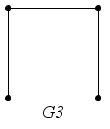
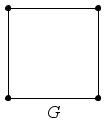
Рис. 34
Определение 4. Граф называется связным, если любую пару его вершин соединяет какой-нибудь маршрут, в противном случае граф называется несвязным.
Например, граф на рис. 33 является связным.
Определение
5.
Орграф называется сильно
связным,
если для любых двух его вершин
 и
и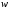 вершина
вершина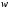 достижима из вершины
достижима из вершины и вершина
и вершина достижима из
достижима из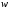 (т. е. между ними существует путь).
Если существует путь из вершины
(т. е. между ними существует путь).
Если существует путь из вершины в
в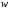 или из
или из в
в ,
то орграф –односторонне
связан.
Орграф называется слабо
связным,
если в графе
,
то орграф –односторонне
связан.
Орграф называется слабо
связным,
если в графе
 существует цепь между вершинами
существует цепь между вершинами иw
(
иw
( – граф, полученный из первоначального
орграфа после отмены ориентации ребер).
– граф, полученный из первоначального
орграфа после отмены ориентации ребер).
Определение 6. Орграф, не являющийся слабо связным, называется несвязным.
Например, на рис. 35: а – сильная связность; б – односторонняя связность; в – слабая связность.
а
б
в
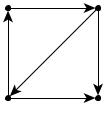
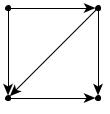
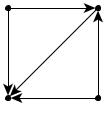
Рис. 35
Определение
7.
Компонентой
связности
графа
 называется его связный подграф, не
являющийся подграфом никакого другого
связного подграфа графа
называется его связный подграф, не
являющийся подграфом никакого другого
связного подграфа графа .
.
Определение
8.
Компонентой
сильной связности (слабой
связности)
орграфа
 называется его связной подграф, не
являющийся подграфом никакого другогоcильного
(слабого) связного подграфа графа
называется его связной подграф, не
являющийся подграфом никакого другогоcильного
(слабого) связного подграфа графа
 .
.
а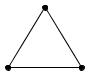 б
б
Рис. 36
Например, граф, изображенный на рис. 36, а, имеет две компоненты связности (рис. 36, б).
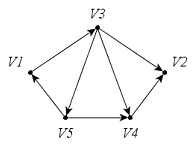
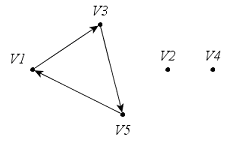
Орграф (рис. 37, а) имеет три компоненты связности (рис. 37, б).
а
б
Рис. 37
Теорема.
Пусть
дан граф
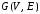 ,
у которого
,
у которого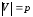 – число вершин,
– число вершин,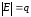 – число ребер,
– число ребер,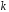 – число компонент связности графа.
Тогда
– число компонент связности графа.
Тогда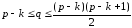 .
.
Следствие.
Если
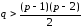 ,
то граф связен.
,
то граф связен.
Вопросы и задачи для самостоятельного решения
Сформулируйте понятие связного графа (орграфа).
Для графов, изображенных на рис. 38, а, б, постройте по четыре подграфа.
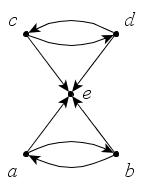
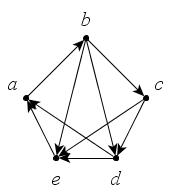
а
б
Рис. 38
Определите связные орграфы. Какие из них являются сильно связными (рис. 39)?
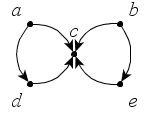
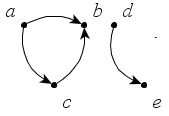
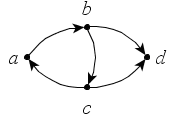
а
б
в
Рис. 39
