Лекция № 8

Функцию распределения можно рассчитать

Вероятность того, что случайная величина попадет в интервал, определяется из общих свойств функцию распределения случайно величины

Если t положить равно 1 , то перепишем следующим образом.

, то вероятность приблизительно 0,68.

Если P- обратная вероятность

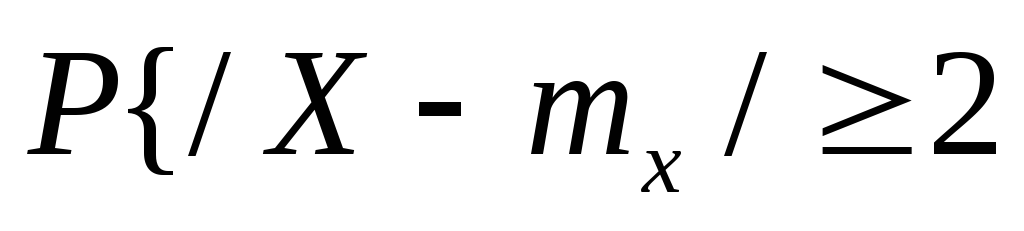
Вероятность того, что = 0,05

Отклонится реализация от математического ожидания на величину больше чем 2.

Если отклонится на 3,то Р=0,01, в этом заключается правило трех сигм.

Из тысячи реализаций одна тысяча попадет в интервал 3. Если определить математическое ожидание случайной величины, определи как интеграл:

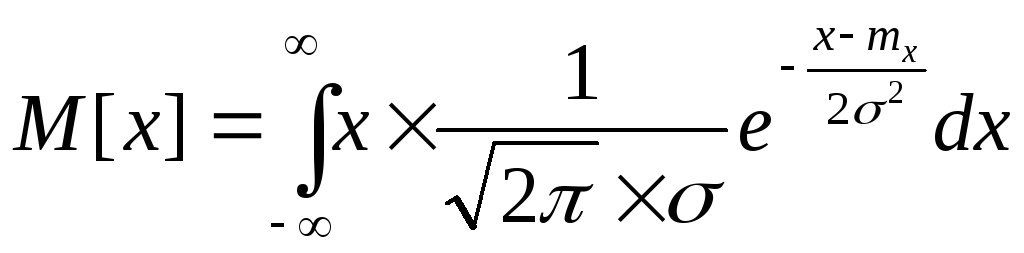
Если взять интеграл по частям, выполнить соответствующие преобразования, интеграл окажется равным

Воспользуемся подстановкой: t=

Параметр распределения , входящий в функцию плотности распределения имеет значение среднего (математического ожидания) случайной величины. Число имеет понятный смысл – это среднее значение математического ожидания.

Если найдем дисперсию (2), найдем смысл параметра. Определение дисперсии случайной нормальной величины ,выполненное по формуле (2) ,показывает смысл второго параметра распределения- среднеквадратичное отклонение или стандартное отклонение. Чем больше, тем больше растянуто распределение.. Зная математическое ожидание и дисперсию, мы грубо оцениваем область наиболее вероятных значений случайной величины: узкая или более широкая область расположения.

Итоговая таблица свойств основных распределений случайных величин.

Наименование случайных величин	Распределение. Формула.	Числовые характеристики
		Мат. ожидание	Дисперсия.
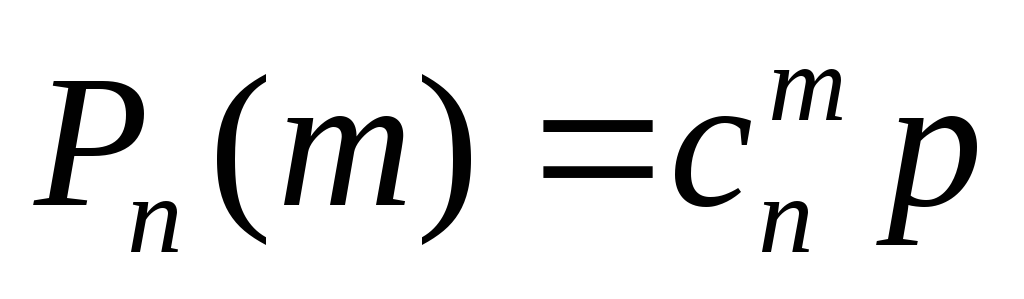
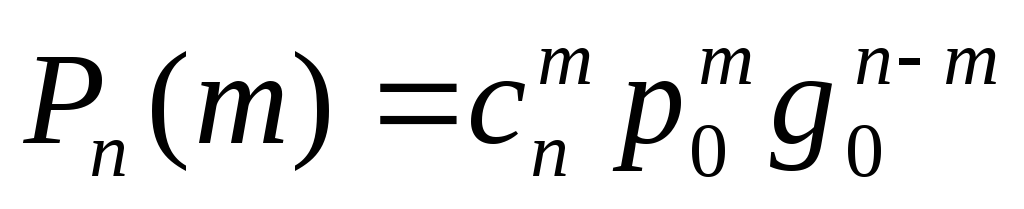
1)Биномиальная случайная величина		n
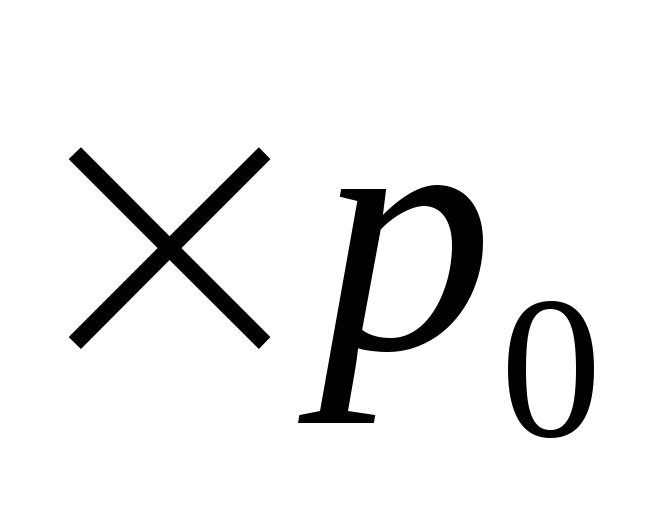
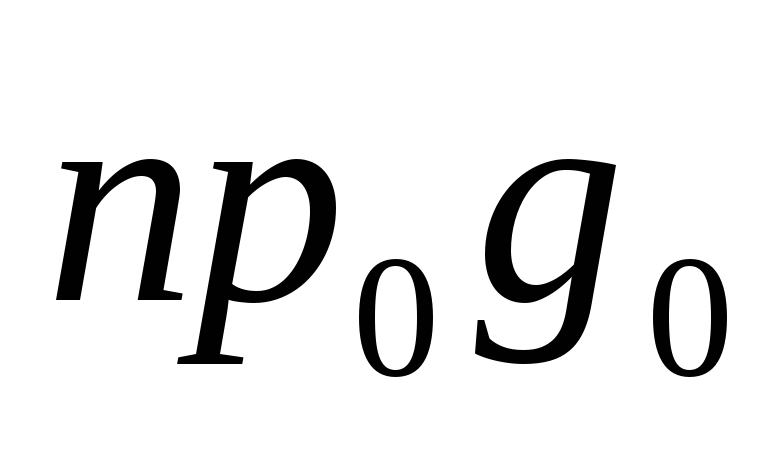
2)Геометрически распределенная случайная величина
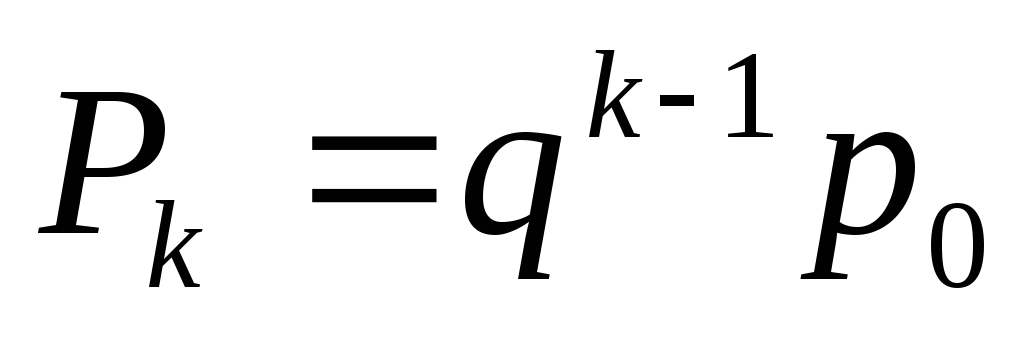
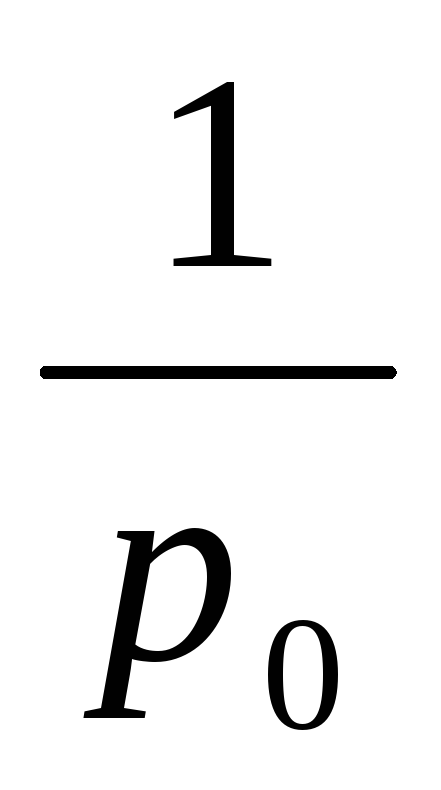
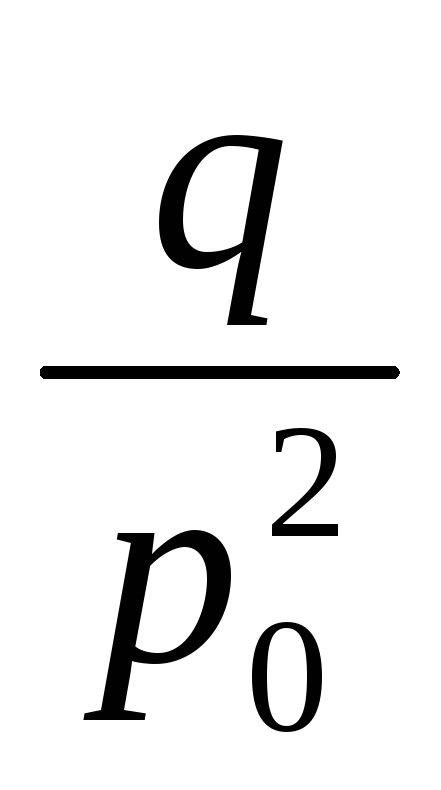
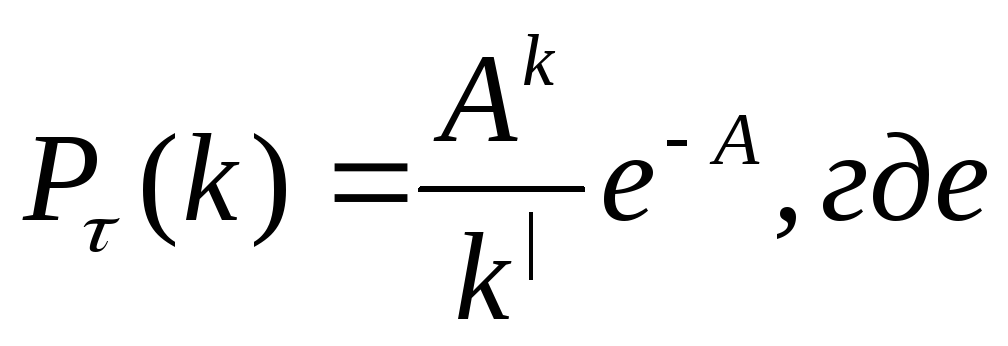
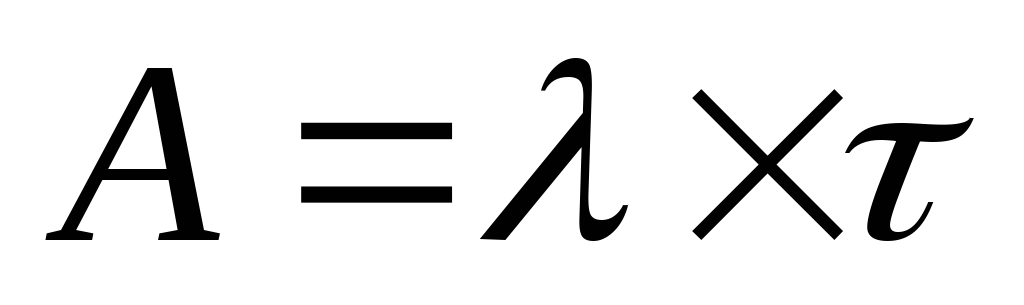
3)Пуассоновская случайная величина		А	А
4)Непрерывная случайная величина (равномерная)
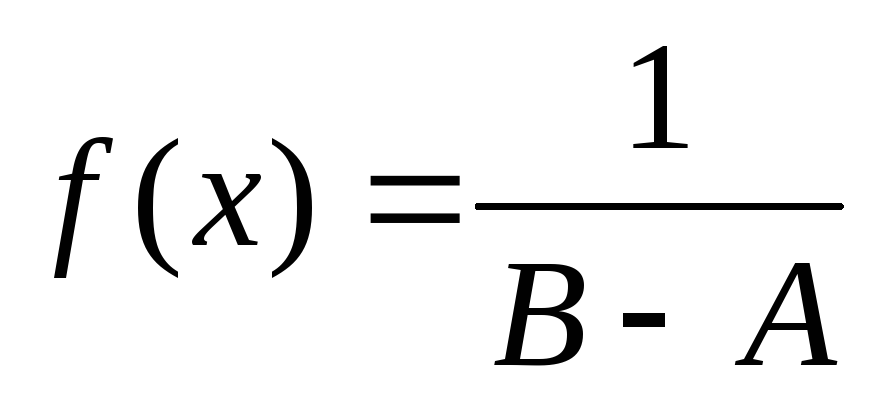
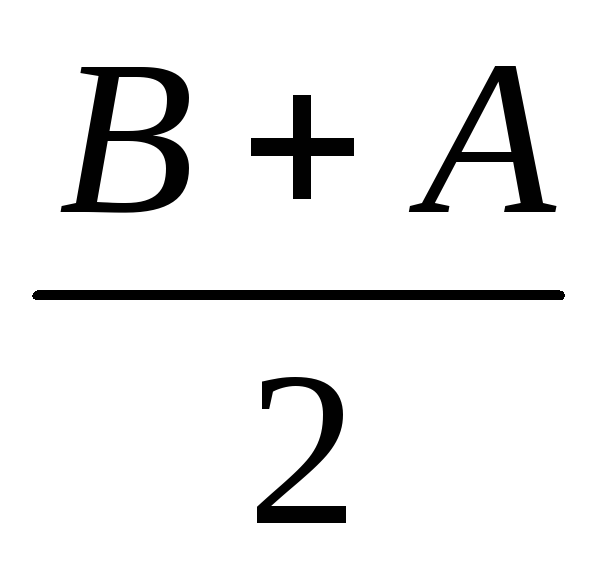
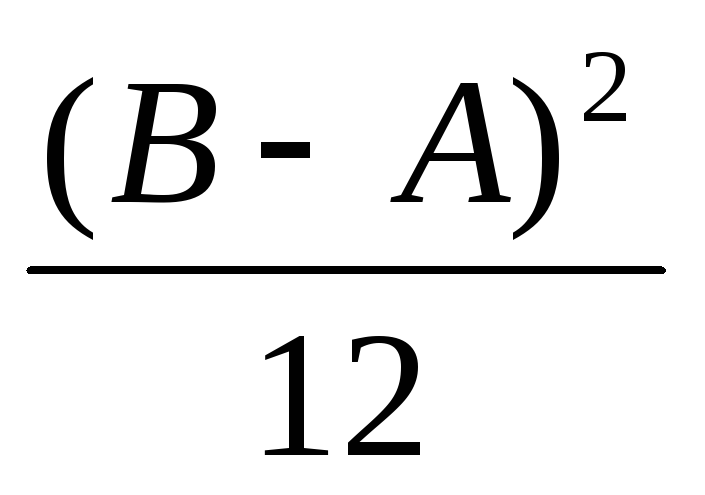
5)Нормальная случайная величина
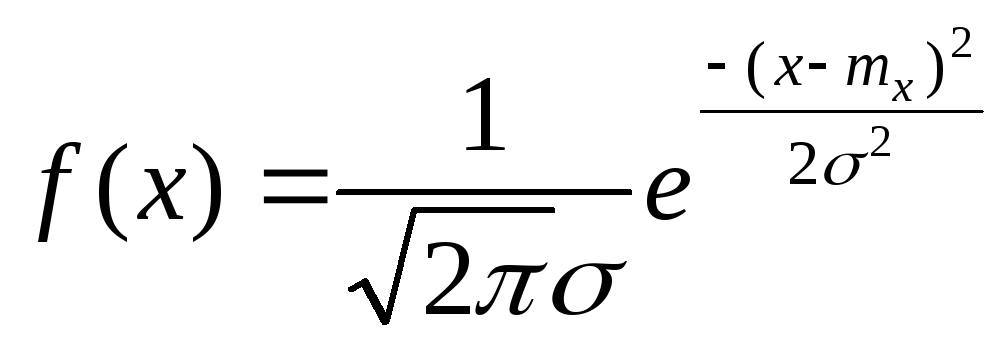
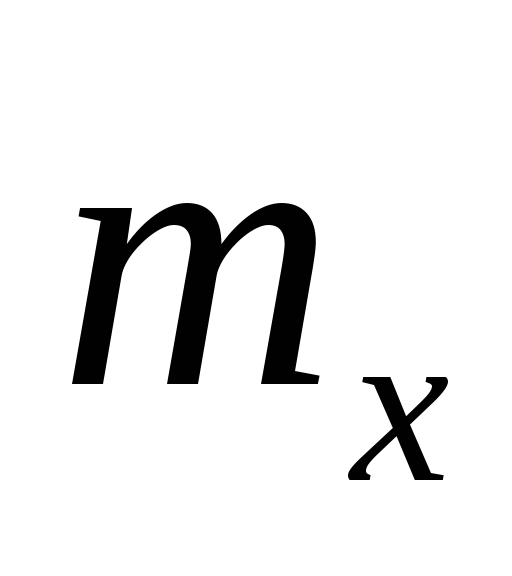
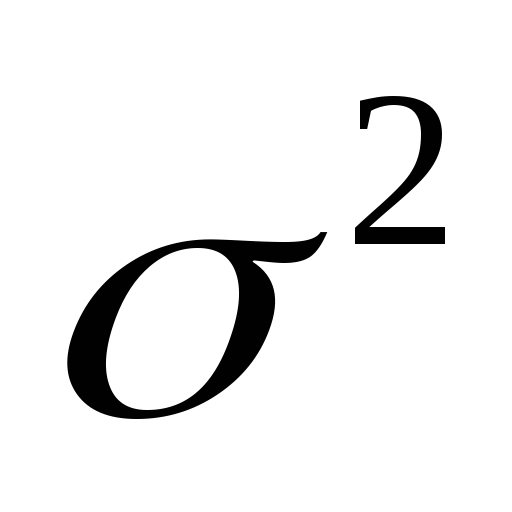
6)Экспоненциальная случайная величина
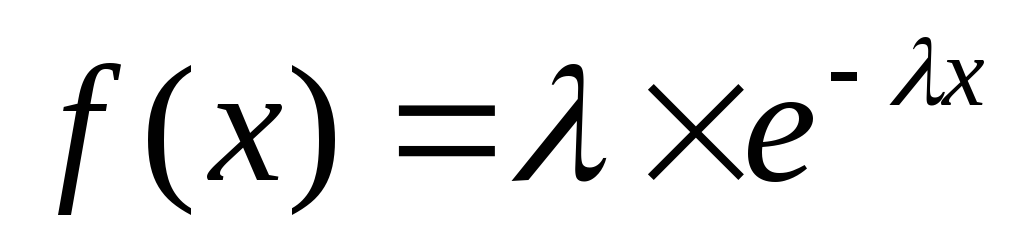
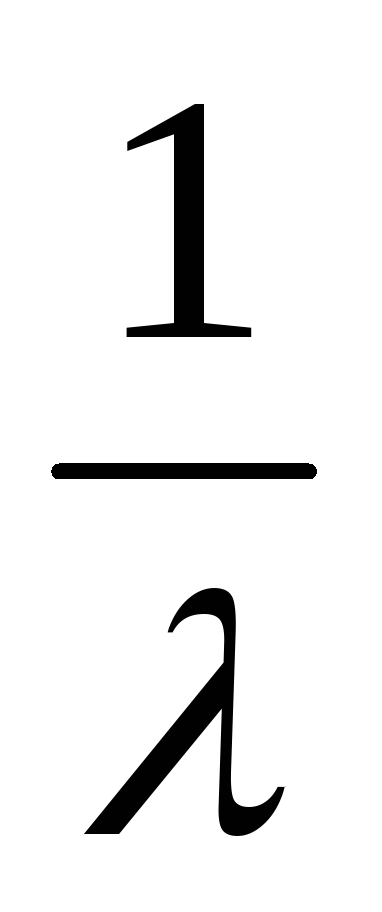
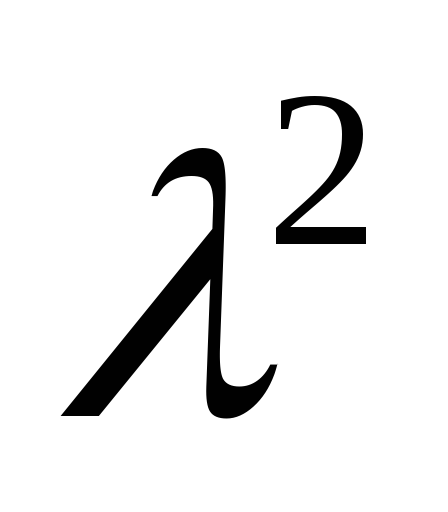
7)Гамма распределение – зависит от 2-х параметров
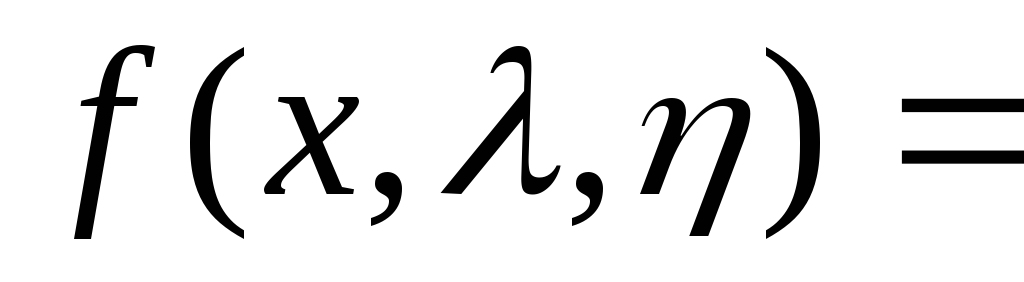
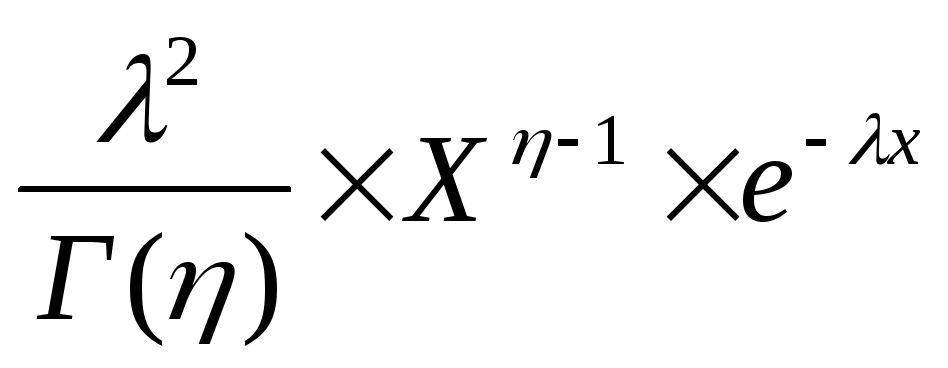
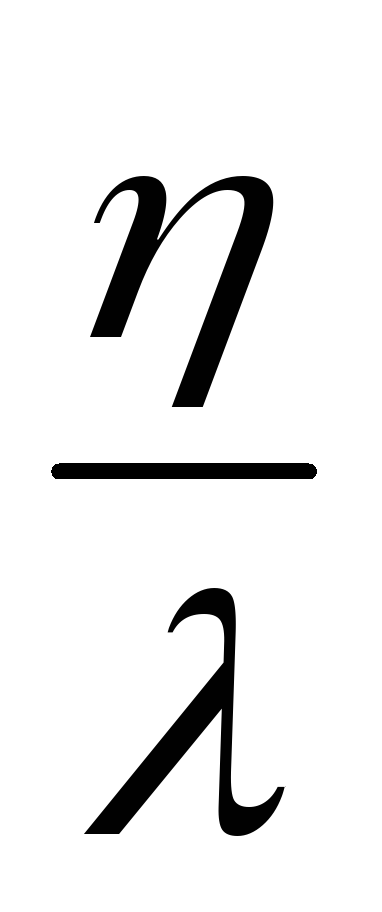
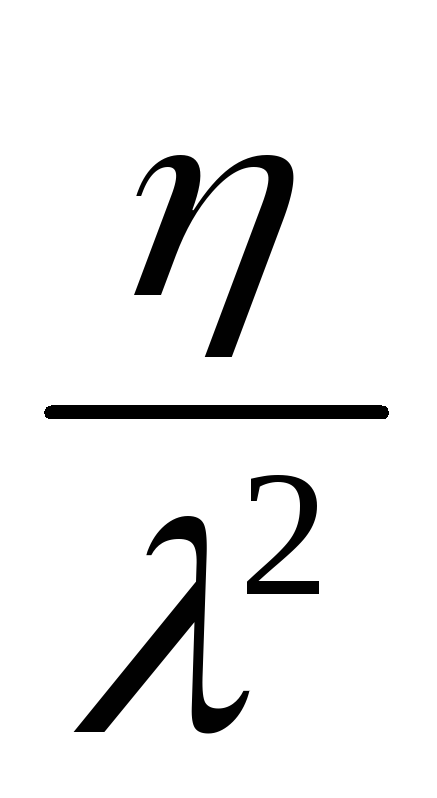
8)Случайная величина Коши (непрерывная)		-----	------

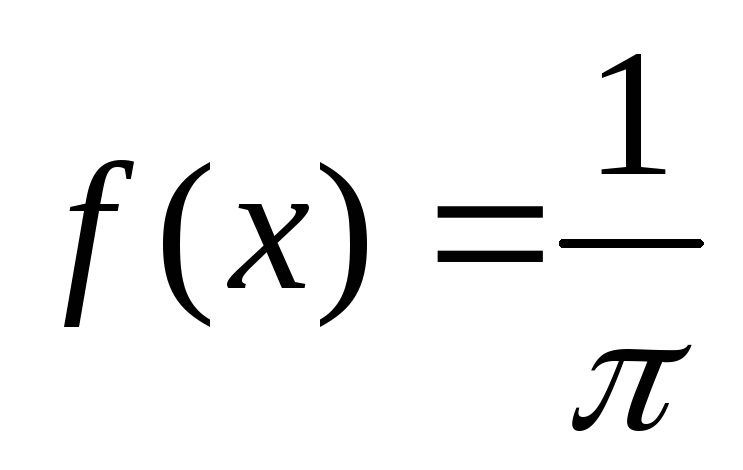
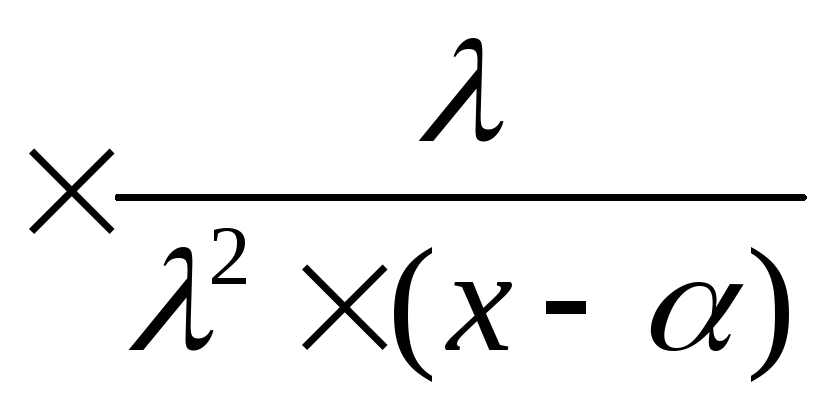
Подбором иможно получить разные графики. Вид графика определяется набороми.

Дополнительные способы описания случайной величины.

Производящие функции в описании свойств случайной величины.

Понятие производящих функций встречается в комбинаторике. Идея механизма производящих функций из комбинаторики, которые позволили упростить перечисление множества объектов.

Различают степенные и моментные производящие функции.

Производящей моментной функцией ПМФ дискретной целочисленной случайной величины z, принимающей значения z=0,1,2… , называют функцию, которая есть математическое ожидание от случайной величины .S – формальная переменная.

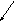
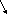
- сумма реализаций самой случайной величины.

Вероятность того, что принять какое-то значение.

Получим функцию, зависящую от распределения S случайной величины. Переходим от набора чисел к функции, которая отражает особенности появления случайной величины на оси z. Мы заменяем неопределенность определенной функцией.

ПМФ – это детерминированная функция аргумента S, она является обобщенным представлением особенности самой случайной величины и вероятностных свойств ее. Если ПМФ известна, то можно найти начальный момент k-го порядка по правилу:

Начальный момент k-го порядка случайной величины z равен k-й произвольной от ПМФ по S, при S=0, то, что получаем и будет k-й момент. Что бы найти математическое ожидание нужно взять момент первого порядка – это степенная производящая функция СПФ.

, где z-та же случайная величина.

СПФ – это математическое ожидание от S в степени. Применяя СПФ, получим общее описание распределения, которое можно заменить одной функцией и работать с ней как с зависимостью изображения от частоты.

Характеристическая функция (ХФ). Вводится для описания особенностей непрерывной величины. С точки зрения математики ХФ – это преобразование Фурье.

f(x) – плотность распределения

w – частота.

Если возьмем первую производную от характеристической функции.

Если возьмем первую производную от характеристической функции по w, w положим равным 0, то в итоге получим математическое ожидание, умноженную на комплексную единицу, можно разделить производную на j, тогда получим результат, который нас интересует.

ХФ используется для описания случайных величин.

Энтропия случайной величины.

Случайная величина – это множество реализаций. Энтропия – характеристика случайной дискретной величины. Есть некоторые наблюдатели. Интерес для наблюдателей представляет: он должен вытащить некоторую случайную величину, после этого должен принимать решение, оно зависит от того, какую реализацию он вытащит. Действие наблюдателя оценивается множеством таких решений. Можно ввести средний риск - отнесенный к одному действию. Средняя неопределенность появления одной какой-либо реализации случайной величины оценивается энтропией.

- определение для дискретной величины.