Лекция №2 Статистическая устойчивость вероятности события.

На практике не всегда случаются случайные события, при анализе которых как число благоприятствующих исходов события, так и общее число исходов ил опытов.

В этом случае необходимо отклонить формулу (1), так как при различных условиях вероятность разная. В этом случае формулой (1) требуется пользоваться с осторожностью. Нужно при нескольких значение посчитать отношение, где n – переменная.

Если стремится к пределу - частота события приn и k может зависеть от опыта и может меняться.

Если при изменении n , то эта называетсяВероятностью события.

Событие А является Статистическим устойчивым. при. Если доказано что событие статистически устойчиво, то можно пользоваться формулой (1).

Понятие вероятности, либо должно быть точно определенно, либо определено для статистических устойчивых событий.

Аксиоматическое определение вероятности (по Колмагорову).

Принципиальная вероятность случайных статистических событий потребовала строгих условий, при которых вероятностные модели получили бы теоретическое обоснование. Эту задачу решил Колмагоров. Он предложил теорию вероятности базировать на следующих аксиомах:

1. рассматривается пространство U. Множество элементарных исходов принадлежит U, каждое событие рассматривается как множество принадлежащее U A U

2. на U задана числовая функция P(A), которая ставит случайному событию в однозначное соответствие число. На P(A) задана числовая функция не меньше 0, но не больше 1. 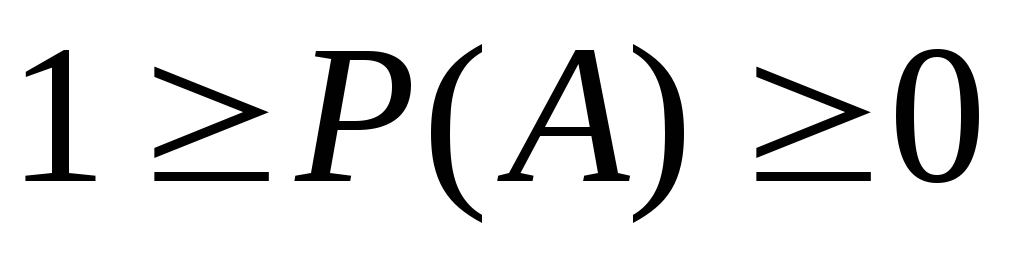- числовая функция – вероятность.

3. Если изменяются два случайных события A и B и они не совместны, то сформируем новое множество A+B P(A+B) и посчитаем вероятности суммы двух несовместных случайных событий P(A+B)=P(A)+P(B) – равна сумме вероятностей этих двух событий.

4. Вероятность 1. Ставим в соответствие множеству исходов множество элементарных исходов.

5. Если есть последовательность убывающих случайных событий

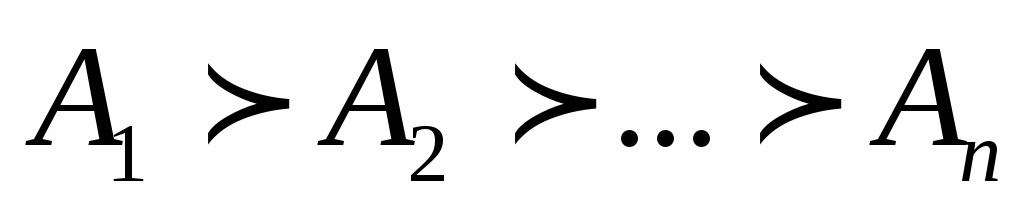
пересечение этих множеств не равно 0, то вероятность события

Элементарные теоремы теории вероятности.

Если более сложные случайные события строятся с использованием операций сложения, умножения, вычитания с некоторыми простыми (исходные, базисные) событиями и для этих простых событий определены вероятности их появления ,то возникает вопрос: “Как, зная вероятности простых событий, определить вероятности сложных событий?”. “Построить” с использованием правил сложения и умножения.

Теорема вероятности полной группы событий.

Пусть имеется два события А и все остальные не , суммы событий образуют полную группу событий. Определим вероятность суммы этих двух событийP(A+)=, по третьей аксиоме

. Событие не является противоположным событию А.

Теорема сложения вероятностей.

Пусть имеется множество событий А и В. Определить вероятность суммы двух событий

P(A+B), тогда A+B=A+B, P(A+B)=P(A)+P(B)B=B+AB

P(B)=P(B)+P(AB); P(B)=P(B)-P(A*B) и подставляем в исходную формулу

P(A+B)=P(A)+P(B)-P(A*B)

Вероятность суммы двух случайных событий, равна сумме вероятностей этих событий и минус вероятность подпроизведения этих событий.

Частный случай, когда случайные события несовместны P(A*B)0, остается P(A)+P(B). Используя связь между вероятностью события А и вероятностью события P(A) и P()

(2)- базируется на результатах теоремы сложения вероятностей, получим теорему “включения и исключения”. Пусть имеется -n случайных событий. Какова вероятность того, что из n событий произойдет ровно r событий? Вероятность того, что в опыте произойдет r событий из указанных n событий определяется формулой “включения и исключения”

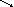Число сочетаний из к по r.

Одни сомножители входят с плюсом, другие с минусом и исключаются. K меняется от r до n. Суммирование проводится по всем возможным размещениям из n по k. K события формируются из одного число событий. Формула является обобщением суммы, появляется возможность использовать формулу произведения.

Теорема умножения вероятностей.

Для того, что бы определить правило отыскания вероятности события, образуемое как произведение нескольких исходных событий следует рассмотреть условную вероятность. Что бы определить построение сложного события нужно ввести дополнительное событие.

Условная вероятность появления случайного события.

В отдельных опытах вероятность искомого события рассчитывается с учетом имеющейся дополнительной информации, которая рассматривается как некоторое условие, при котором может произойти интересующие нас событие. Вероятность появления события при описанных условиях и называется условной вероятностью события.

Есть событие А, при котором происходит событие В. Запишем условную вероятность события В, при условии А. , в соответствии с определение вероятности посчитаем эту вероятность.число благоприятствующих событий В по общему числу событий. Это есть мощность множества А на В, т.е. происходит и событие А и В. Разделим на общее число исходов, т.е. на мощность события А.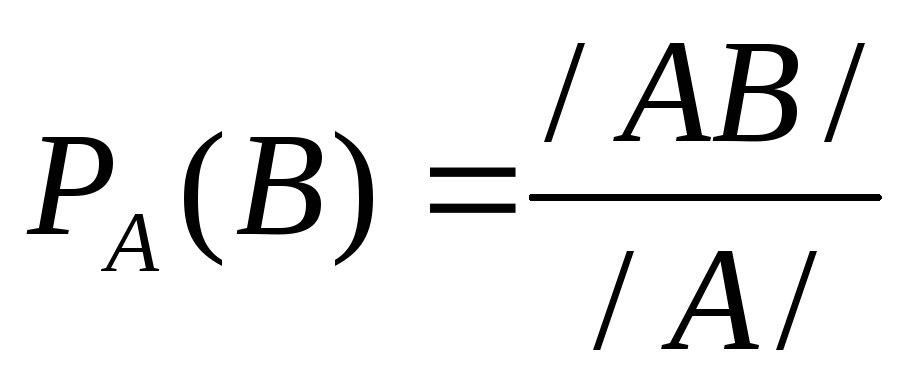, перейдем от мощности событий к вероятности, поскольку они определены на множестве, то разделим на мощность множестваи числитель, и знаменатель.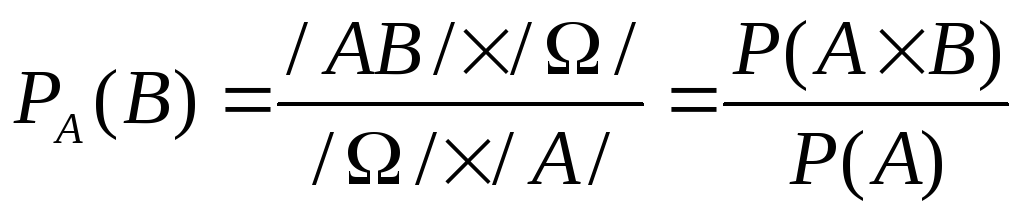, отсюда вытекает правило определения вероятности произведения двух событий – это вероятность события А, на условную вероятность события А на В.

(3) Вероятность произведения двух событий равна вероятности события А на условную вероятность события В, при условии, что событие А произошло. Можно записать (4) = вероятности одного события на условную вероятность другого, при условии, что первое произошло. На основе теоремы вероятности формируется понятие зависимых и независимых случайных событий. Если в формуле (2) условная вероятностьP(B) не зависит от условия А ,то события А и В являются независимыми и формула упрощается.

- равно произведению этих событий , когда события независимы, т.е. это частный случай.

Рассмотрим общий случай, когда ищется вероятность произведения n – событий. Пользуемся предшествующим результатом (формулой 4). Выделяем n-1 событие ,а последнее событие как n.

, если независимые