Функция распределения для непрерывной случайной величины

F(x)

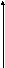
x

a b

Из общих свойств F(а) = 0; F(b) = 1. Если рассматривать абсолютно непрерывную случайную величину, то F(а) – монотонно возрастающая функция. Вероятностные свойства можно найти, если найти приращение в точках; разделим на приращение аргумента, проанализируем это приращение:

lim ∆F(x) / ∆x = f(x)

^{∆x→ 0}

f(x) = dF(x) / dx

- производная функции F(x) - есть плотность распределения непрерывной случайной величины.

Плотность распределения непрерывной случайной величины – есть вероятность того, что реализация непрерывной случайной величины попадет в единичный интервал в окрестности выбранной точки x.

Зная плотность распределения F(x), можно найти саму функцию:

_x

F(x) =∫ f(x) dx

^a

А плотность распределения вызывает интерес в практических задачах.

P{x = c} = 0

P{α ≤ x ≤ β } = F(β) – F(α)

P{c ≤ x ≤ c + ∆x} ≈ f(c) ∆x

Вывод: применение плотности распределения случайной величины F(x) позволяет уточнить местные вероятностные свойства случайной величины.

Лекция №6 Числовые характеристики случайной величины

Рассмотренные в предыдущем параграфе вероятностные характеристики случайной величины дают полное описание вероятностных свойств случайной величины. В практике анализа исследования случайных величин обладают меньшим объемом сведений. В таких ситуациях прибегают к использованию интегральных свойств случайной величины и говорят об интегральном описании случайной величины. К таким интегральным характеристикам относятся числовые характеристики случайной величины. Они делятся на:

1. характеристики положения характеризуются расположением случайной величины вдоль оси х;

2. моментные характеристики отражают особенности графика, отражено либо плотность распределения или закон распределения;

Представления о свойствах прямой.

Числовые характеристики, относящиеся к характеристикам положения.

Медиана (Ме) – есть такое значение, для которого вероятность случайной величины меньше или равно значения медианы:

P{x ≤ Me} = P{x > Me}

х - такое значение случайной величины, для которой вероятность какой-то реализации будет меньше медианы. Медиана может совпасть с какой-то реализацией.

P_i

P₁

P_i-1 P_n

P_i-2

… …

Сточки зрения моды отличают одномодальную случайную и другие многомодальные. Мода определяется из условияf(x) = 0

f(x)

x

0

Моментные характеристики

Моментные характеристики являются аналогом использования теоретической механики, понятием центра тяжести фигуры, центр масс кривой. Рассмотрим начальные моменты. Если рассматриваются дискретные случайные величины.

_n

М^(k)[X] = μ_k = ∑ x_i^k P(x_i) k=1,2

ⁱ⁼¹

k – порядок;

x_i^k - i-я реализация случайной величины х;

P(x_i) – вероятность этой реализации;

n – число реализаций.

Характеризует центр случайной величины М[x] = М_i

x

х₁ х₂ х_i х_n

_n

∑ x_i P(x_i)

ⁱ⁼¹

Первый начальный момент называют математическое ожидание случайной величины. Смысл мат. ожидания дает пример усреднения вероятностного объекта случайной величины.

Вычисляя мат. ожидание мысленно осуществляем замену:

М[x] m_x

Чтобы получить представление о случайной величине действуем оператором М – мат. ожидание. Действие этого оператора будем называть математическим ожиданием. В результате действия математического ожидания мы получаем число m_{x .}

μ^k [x] с целью получения уточненного описания свойств случайной величины. В самом первом приближении часто используют математическое ожидание. Если рассматривается непрерывная случайная величина, случайные моменты k-го порядка, то правила определения этих порядков следующие:

_b

М_к^(к) [X] = ∫ x^k f(x) dx ;

^a

где a,b – область значения случайной величины.

Найдем математическое ожидание: _b

М [X] = ∫ x f(x) dx

^a