Примеры распределения случайной величины.

Среди бесконечного набора случайных величин необходимо выбрать один набор.

В последовательности, в серии из n испытаний успех произойдет ровно n раз и определяется формулой.

Д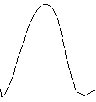ля дискретной случайной величины задается закон распределения.

p

m=n

Зависит от и от того, какова длинна серии. С увеличениеn появляется ассиметричный график, который круче изменяется.

Математическое ожидание -

Дисперсия -

Геометрически распределенная случайная величина.

так же определена на схеме Бернулли, последовательности из n испытаний. Успех произойдет первый раз на k – м шаге. Поскольку результаты испытаний не зависят друг от друга, необходимо, что бы на k-1 предыдущем шаге, успех не произошел, а на k-м шаге он произошел, такую величину называют геометрически распределенной.

q=1-p

- математическое ожидание.

- дисперсия.

Гипергеометрическое распределение.

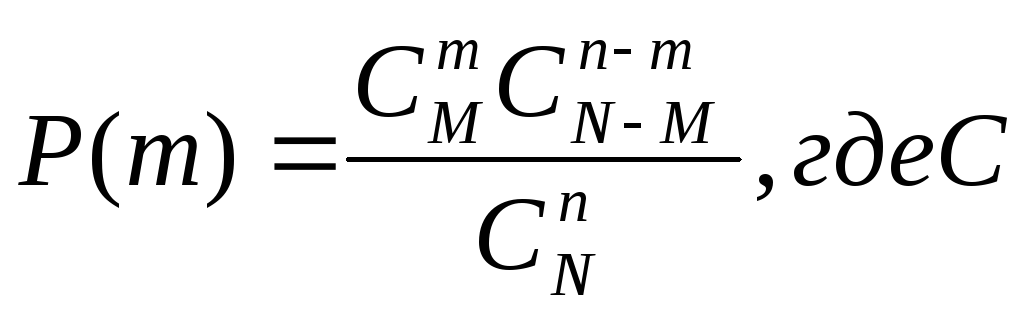
- число способов, которыми можно вытащить черные шары.

- число способов, которыми можно сформировать выборку.

Случайная величина, распределенная по закону Пуассона.

Поясняется следующей схемой. На примере рассматривается ось времени, определяется интервал длинной . В любой точки оси может произойти некоторое случайное событие. На интересующем нас интервале произойдет ровно k событий.



   t

Требуется определить вероятность этого события, что бы это сделать, нужно ввести уточнения в особенности появления элементарных событий на оси времени t. Обычно рассматриваемую последовательность элементарных событий на оси времени t называют потоком случайных событий. Нужно уточнить особенности рассматриваемого потока событий. Пуассоновская случайная величина порождается простейшим (Пуассоновским) потоком. Это означает, что поток событий обладает тремя свойствами:

1. свойство ординарности потока. Означает, что если выберем малый интервал  равный 0, то вероятность того, что на этом интервале произойдет 2 и более событий равно 0.

. На этом интервале может произойти либо 1, либо 0 – не произойти. Такие потоки называют редкие потоки.

2) свойство стационарности. Вероятность того, что событие произойдет на интервале не зависит от того, на каком месте осиt расположен этот интервал *.

3) отсутствие последствия. Если на оси t возьмем два интервала, например, , что бы они не пересекались, то вероятность того, что событие произойдет на одном интервале, не зависит от того, произошли ли они на другом, напримерили нет. Если поток обладает такими свойствами, то Пуассон установил такое выражение, что бы определить вероятность такого события. На интервале произойдет ровно k событий определиться формулой:

Вероятность того, что событие произойдет на единичном интервале времени, поскольку и известные величины, то , то

Случайная пуассоновская величина обладает свойством, что ее математическое ожидание и дисперсия равны а.

С пуассоновской случайной величиной связана непрерывная случайная величина. Если рассматривать время - интервал времени между событиями, тогда сформируем непрерывную случайную величину.

Примеры непрерывных случайных величин.

В схеме Пуассона непрерывная случайная величина, представленная на рисунке описывается таким распределение: f(t) – плотность функции распределение непрерывной случайной величины, заданной в схеме Пуассона.

- введенная случайная величина имеет такую плотность распределения.

Когда речь идет о непрерывной случайной величине. Величина, определяющаяся данным объемом, называется экспоненциальной или показательной случайной величиной Х.

График функции

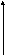
х

Функцию распределения получаем как:

Некоторые числовые значения.

Равномерная случайная величина.

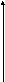В области возможных значений случайной величины плотность должна оставаться постоянной

F(x)

с

а в х

.

Аналогически можно записать:

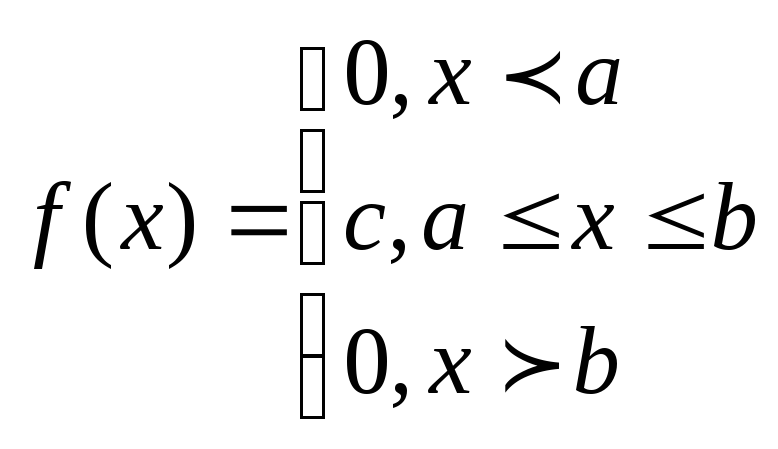
График плотность следующий: строим функцию распределения.

1

Рис.1

График не может превышать 1, строится по линейному закону (рис.1). Рассчитаем математическое ожидание.

- среднее значение.

Случайная величина, распределенная по нормальному закону.

Она является своеобразным эталоном случайных величин. В качестве первого приближения используют эту величину.

Рассмотрим свойства нормальной случайной величины:

1)начинаем с определения плотности распределения f(x) и описывается следующей формулой.

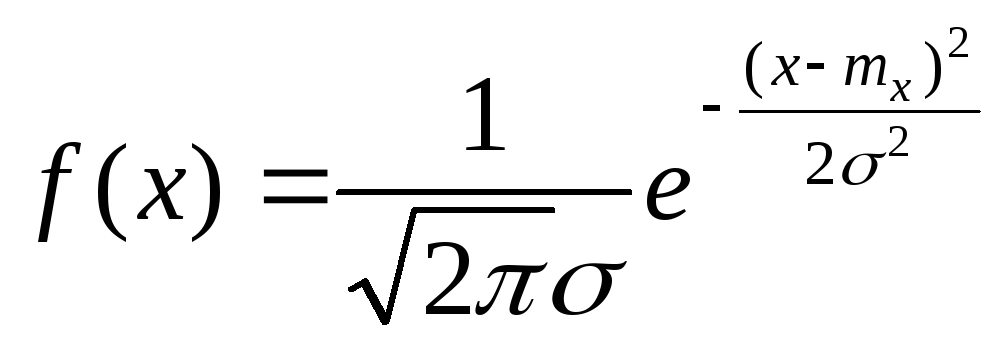
Строим график.

1. реализации случайных величин могут принимать значения от [-;]

-

Рисуем симметрично .

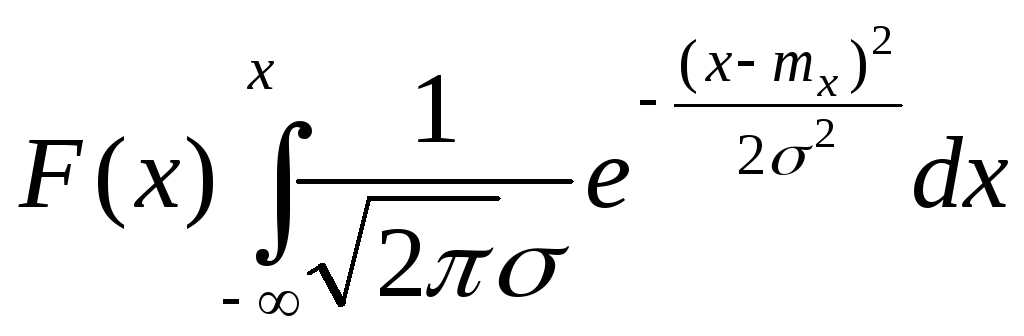
Значение можно выразить через вспомогательную функцию. Вводим вспомогательную переменную .

Значения этой функции составлены в виде таблице. Если выразить F(x) через Ф(t) , можем выразить любое t, тогда если подставим, то получим соотношение. В целом удобно представить вероятностные свойства в виде случайной величины и в виде графика .

1

0,5

-3-2-++2+3

Записываем вероятности следующих событий - вероятность того, что отклонение будет меньшеt, а если t равно 1 , то берем интервал от -2 до -.

Если t равно 1 то p=0.24

Если t равно 2 то p=0.54

Если t равно 3 то p=0.99

Правило трех сигм

Теоретически случайная величина находится в интервале [-;], а с помощью этого правила она попадает в интервал [-3;+3]. В этом смысл правила трех сигм, особенно случайной величины.