Лекция № 12 Центральные предельные теоремы

Центральные предельные теоремы относятся к теоремам, которые обосновывают возможность нахождения функции распределения по совокупности экспериментальных данных. Простейшая интерпретация обычно связывают со следующим утверждением: если имеется система последовательных одинаково распределенных случайных величин, при этом предполагается, что они распределены по нормальному закону, то распределение суммы также подчиняется нормальному закону. Это утверждение достаточно часто используют на практике, когда исследуемая случайная величина представляется в виде суммы некоторого числа исходных случайных величин, которые имеют нормальное распределение. В общем случае, если случайные величины не имеют нормального распределения, т.е. распределены по какому-то другому закону, вводят в рассмотрение нормированную случайную величину:

_k

η_i = B^-1 ∑ (x_i - m_i)

ⁱ⁼¹

где x_i - последовательность из k случайных величин;

_k

∑ (x_i - m_i) – сумма центрированных случайных величин;

ⁱ⁼¹

_k

B² = ∑σ_i² – сумма дисперсий.

ⁱ⁼¹

F(η) – закон распределения суммы нормированных случайных величин.

| F(η) – Φ(x) | ≤ A

Все случайные величины, входящие в сумму имеют одинаковые математические ожидания. n – число случайных величин, входящих в сумму.

Φ(x) =

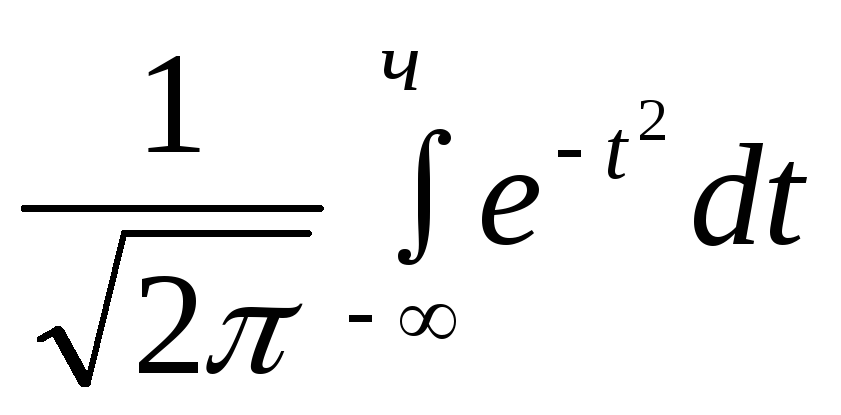
Отклонение зависит от центрального момента 3-го порядка. Если мат. ожидание разное для случайной величины, то

| F(η) – Φ(x) |= A

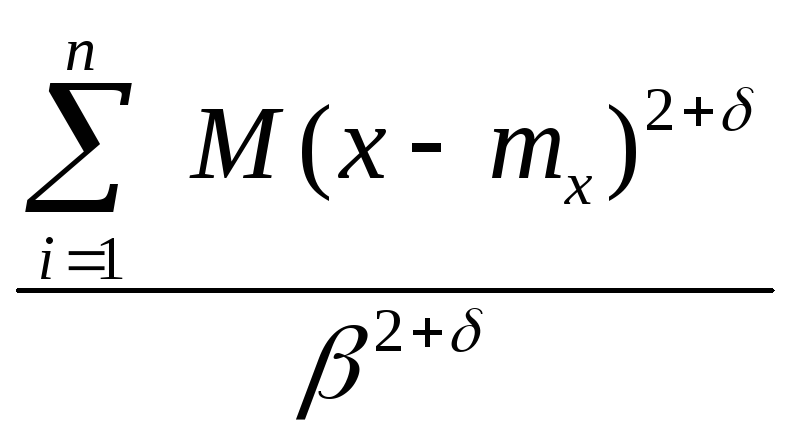
Вводится постоянная величина δ, если δ = 1 и мат. ожидание одинаково, то получаем

_k

B² = ∑σ_i² δ = 1.

ⁱ⁼¹

Приблизительно одинаковые дисперсии. Отличие изучаемой случайной величины от известной. В качестве примера центральной теоремы можно назвать интегральную локальную теорему Муавра-Лапласса.

Вводим случайную величину x =

тогда f(x) = e^-

Случайные процессы

Это следующая вероятностная модель, которая определяется через понятие случайной функции – аргумента ψ (θ) ставит в однозначное соответствие фиксированному значению аргумента ψ случайную величину.

ψ (θ_i) = X_i

X_i – это множество чисел.

Случайная функция базируется на применении случайной величины. Если в качестве аргумента ψ выступает время , то мы имеем дело со случайным процессом ψ (t) = x(t).

Рассмотрим 2 схемы, объясняющие что такое случайный процесс.

Способы представления (объяснения) случайного процесса

Два способа описания представления случайного процесса:

1. Основан на определении случайного процесса и использует введенные вероятностные модели. Случайный процесс описывает явление, развивающиеся во времени. Выделим точку, в которой должны наблюдать за случайным процессом. Обращаемся к определению случайного процесса. Зафиксируем значение аргумента.

ψ (t) = x(t), x(t₀) = X₀

Зафиксировали t₁, получаем другую случайную величину x_1. Случайная величина превратилась в непрерывную случайную величину. При таком представлении случайный процесс рассматривается как определенная на оси времени последовательность случайных величин - систему случайных величин. Каждая случайная величина в системе называется сечением случайного процесса.