
Левченко 2 часть
.pdf81
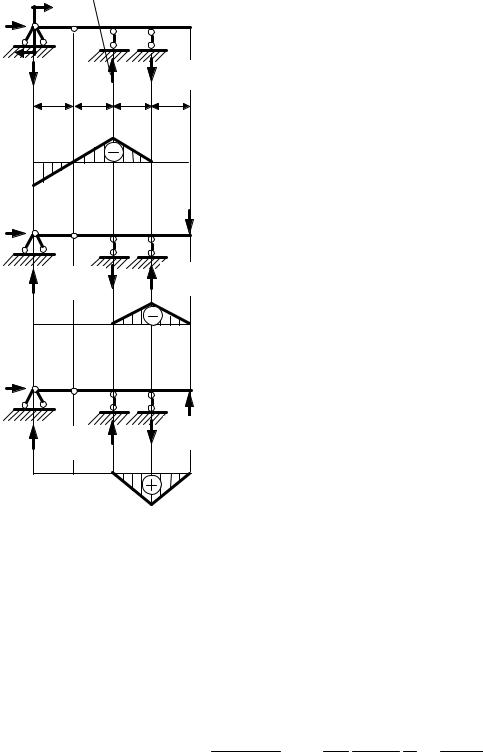
ризонтальная реакция НА в балках при отсутствии горизонтальной составляющей нагрузки всегда равна нулю – это следует из уравнения равновесия "сумма проекций всех сил на горизонтальную ось равна нулю". Для определения трех других опорных реакций RA, RB и RC составим три уравнения равновесия:
∑mEслева = 0 ; |
M + RAa = 0 ; |
RA = −M / a ; |
∑mB = 0; |
M + RA 2a − RC a = 0 ; |
RC = −M / a ; |
∑mC = 0 ; |
M + RA 3a + RBa = 0; |
RB = 2M / a . |
|
|
|
|
|
82 |
|
|
|
|
|
|
|
|
а |
М |
|
RB= 2M/a |
При |
составлении уравне- |
||||||||
|
ний статики было принято, что |
||||||||||||
HA=0 A |
E |
B |
C |
|
все реакции действуют вверх, |
||||||||
|
|
|
|
|
|
полученные знаки учтены в на- |
|||||||
RA= M/a |
|
|
|
RC= M/a |
правлении |
|
реакций |
на |
|||||
|
|
а |
а |
а |
а |
рис. 4.38, а. |
Первое |
уравнение |
|||||
|
|
|
|
М |
|
равновесия связано с наличием |
|||||||
б |
|
|
|
|
шарнира в точке Е балки и по- |
||||||||
|
|
|
|
эпюра ММ |
|||||||||
|
М |
|
|
|
казывает, что изгибающий мо- |
||||||||
в |
|
|
|
|
мент в шарнире равен нулю, то |
||||||||
HA=0 A E |
B |
C |
D 1 |
есть сумма моментов всех сил |
|||||||||
|
|
|
|
|
|
слева (или справа) от шарнира |
|||||||
RA= 0 |
RB= 1 |
|
RC= 2 |
равна |
нулю. |
Эпюра |
изгибаю- |
||||||
а |
щих моментов ММ от заданной |
||||||||||||
г |
|
|
|
|
|||||||||
|
|
|
|
эпюра М1 |
нагрузки |
|
показана |
на |
|||||
|
|
|
|
|
|
||||||||
д |
|
|
|
|
|
рис. 4.38, б. |
Чтобы |
|
построить |
||||
HA=0 A |
E |
B |
C |
D |
эпюру изгибающих |
моментов |
|||||||
от единичной обобщенной си- |
|||||||||||||
|
|
|
|
|
Х |
лы, приложим эту силу к балке. |
|||||||
RA= 0 |
|
|
|
RC= 2X |
|||||||||
RB= X |
|
Поскольку определяем прогиб в |
|||||||||||
е |
|
|
|
|
эпюра МХ |
точке D, то согласно методу |
|||||||
|
|
|
|
|
Максвелла – Мора прикладыва- |
||||||||
|
|
|
|
|
Ха |
ем в точке D сосредоточенную |
|||||||
|
Рис. 4.38. Схемы балки и эпюры |
силу, |
|
равную |
|
единице |
|||||||
|
изгибающих моментов: |
(рис. 4.38, в). Находим опорные |
|||||||||||
|
а, б – от заданной нагрузки; |
реакции и строим эпюру М1 |
|||||||||||
|
в, г– от единичной силы; |
аналогично выполненному |
ра- |
||||||||||
|
д, е– от лишней неизвестной |
нее |
построению |
эпюры |
ММ |
||||||||
|
|
|
|
|
|
(рис. 4.38, г). |
Вычисляем |
про- |
|||||
гиб в точке по формуле Максвелла – Мора, перемножая эпюры ММ и |
|||||||||||||
М1: |
|
|
|
|
|
|
|
|
= Ma2 . |
|
|
||
|
|
|
|
wD (M ) = ∫ M M M1dx = 1 M a a |
|
|
|||||||
|
|
|
|
|
EI |
EI |
2 |
3 |
6EI |
|
|
|
|
|
|
|
|
|
|
83 |
|
|
|
|
|
|
|
|
Теперь ищем прогиб в точке D от лишней неизвестной Х – |
||||||||||||||
wD ( X ) . Строим эпюру МХ |
(рис. 4.38, е) и перемножаем ее с эпюрой |
|||||||||||||
М1, пользуясь правилом Верещагина: |
|
|
|
|
|
|
2 Xa3 . |
|||||||
|
wD |
( X ) = ∫ M X M1dx = − |
1 Xa a 2 a |
2 = − |
||||||||||
|
|
|
|
EI |
|
EI |
2 |
|
3 |
|
3EI |
|
||
Складываем wD (M ) и wD ( X ) , находим полное перемещение и |
||||||||||||||
в соответствии с условием совместности деформаций приравниваем |
||||||||||||||
его нулю: |
|
|
|
|
|
Ma2 |
|
2 Xa3 |
|
|
|
|
|
|
|
|
|
|
wD = |
− |
= 0 . |
|
|
|
|||||
|
|
|
|
6EI |
|
3EI |
|
|
|
|||||
Отсюда X = M . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4a |
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, мы нашли лишнюю неизвестную Х из условия совместно- |
||||||||||||||
сти деформаций. Прикладываем ее к заданной системе, не меняя на- |
||||||||||||||
правления, так как значение Х получилось положительным. Строим |
||||||||||||||
окончательные эпюры внутренних усилий и от заданных нагрузок |
||||||||||||||
(пары сил М), и от лишней неизвестной Х. Эти эпюры показаны на |
||||||||||||||
|
M |
|
|
|
|
|
|
|
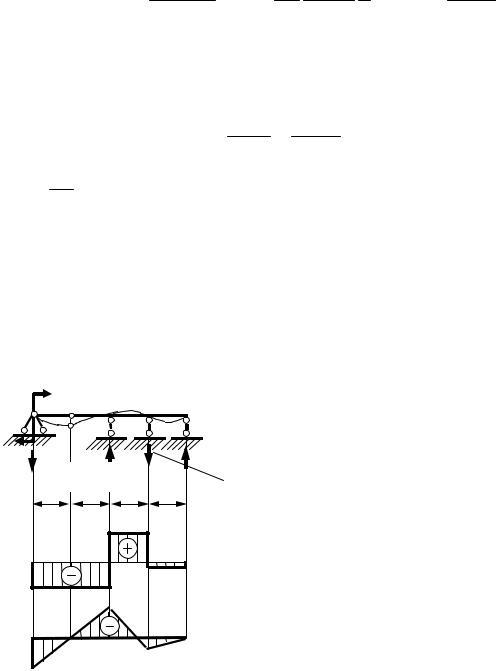
рис. 4.39, б, в. |
|
|
|||
a |
|
|
|
|
|
|
|
|
|
Заканчиваем |
решение |
|||
A E |
|
B |
C |
D |
|
|
|
проверкой результатов. Час- |
||||||
|
|
|
|
|
X= M/4a |
|
|
то можно обнаружить ошиб- |
||||||
RA= M/a |
|
|
|
|
|
|
ку, если построить изогну- |
|||||||
RB= 9M/4a |
а |
RC= 3M/2a |
|
тую |
ось |
балки. Изогнутая |
||||||||
|
а |
а |
а |
|
ось |
|
должна |
удовлетворять |
||||||
б |
5M/4a |
|
|
|
|
|
как эпюре моментов, кото- |
|||||||
|
|
|
|
M/4a |
|
|
рая показывает, в какую сто- |
|||||||
M/a |
|
|
|
|
Эпюра Q |
|
|
рону |
направлена |
выпук- |
||||
|
|
M |
|
|
|
|
|
лость оси балки после изги- |
||||||
|
|
|
|
|
|
|
|
|||||||
в |
|
|
|
|
Эпюра М |
|
|
ба, |
так и условиям закреп- |
|||||
|
|
|
|
|
|
|
ления балки. На рис. 4.39, а |
|||||||
M |
|
|
|
4 |
|
|
|
|
||||||
|
|
|
|
|
|
|
показана |
деформированная |
||||||
|
|
|
M/ |
|
|
|
|
|||||||
Рис. 4.39. Окончательные эпюры |
|
|
ось балки, удовлетворяющая |
|||||||||||
|
|
указанным условиям. Заме- |
||||||||||||
внутренних усилий в заданной балке |
|
|
тим, что из-за наличия шар- |
|||||||||||
|
|
|
|
|
|
|
|
|
нира возможен перелом изо- |
|||||
84
гнутой оси в точке Е, так как сечения, примыкающие к шарниру поворачиваются на разные углы. Если не удается построить изогнутую ось так, чтобы она удовлетворяла всем условиям, то следует искать ошибку. Эта проверка носит качественный характер и не всегда дает возможность найти ошибку в вычислениях. Проверкой, подтверждающей правильность вычисления лишней неизвестной, является условие (4.29), то есть результатом перемножения окончательной эпюры М с эпюрой изгибающих моментов от единичной обобщенной силы М1 (по правилу Верещагина) должен быть ноль. Делая эту проверку, мы еще раз проверяем равенство нулю прогиба в точке D в нашей задаче, поскольку смыслом этого перемножения является согласно методу Максвелла – Мора определение перемещения по направлению обобщенной силы (прогиба в точке D в решаемой задаче). Проверим решение нашей задачи:
|
M M |
1 |
|
1 |
|
M a 2 |
|
a |
|
|
M |
|
|
Ma2 |
|
|
Ma2 |
= 0 . |
||||
∫ |
|
dx = |
|
− |
|
|
|
|
|
a + |
|
|
−2 |
|
a + Ma |
= − |
|
+ |
|
|
||
EI |
|
|
4 2 3 |
6 |
4 |
12EI |
12EI |
|||||||||||||||
|
|
|
EI |
|
|
|
|
|
|
|
||||||||||||
4.3.2. Расчет статически неопределимой рамы (задача № 24)
Условие задачи
В раме, показанной на рис. 4.40, требуется определить внутренние усилия и построить ось рамы после деформации. Жесткость всех стержней рамы одинакова и равна EI.
Решение
Рассматриваемая рама является один раз статически неопределимой и для выбора основной системы требуется отбросить одну лишнюю связь. Такой лишней связью будем считать шарнирно-

|
85 |
|
|
|
|
|
|
|
|
В |
подвижную опору в точке В. Ос- |
||||||||
М=30 кН·м |
новная |
система |
с |
отброшенной |
|||||
лишней |
связью |
показана |
на |
||||||
3м |
|||||||||
рис. 4.41. |
Лишняя неизвестная, |
то |
|||||||
|
есть реакция в отброшенной лиш- |
||||||||
F=20 кН |
ней связи, обозначена буквой Х. Ус- |
||||||||
|
ловие |
совместности |
|
деформаций |
|||||
3м |
для выбранной основной системы – |
||||||||
это условие, приравнивающее нулю |
|||||||||
А |
горизонтальное перемещение точки |
||||||||
В: δгорB = 0 . Это перемещение скла- |
|||||||||
3м |
дывается из перемещения, вызван- |
||||||||
|
ного |
всей |
заданной |
нагрузкой |
|||||
Рис. 4.40. Схема рамы с нагрузками |
δгор(P) , и перемещения от лишней |
||||||||
B |
|
|
|
|
|
|
|
||
неизвестной δгорB ( X ) . Тогда условие со-
вместности деформаций запишем так:
δгорB (P) + δгорB ( X ) = 0.
Будем искать перемещения методом Максвелла – Мора с использованием правила Верещагина. Для этого построим три эпюры изгибающих моментов в основной системе: от заданной нагрузки (рис. 4.42, а), от единичной силы, соответствующей горизонтальному перемещению в точке В (рис. 4.42, б), и от лишней неизвестной Х (рис. 4.42, в).
 В Х М=30 кН·м
В Х М=30 кН·м
F=20 кН
А
Для определения δгорB |
(P) перемножим |
эпюры МР и М1: |
Рис. 4.41. Основная система |
δгорB (P) = ∫ MEPIM1 dx = EI1 (−30 3 1,5 − 30 3 3 − 302 3 4 − 902 3 5) =
=−1260EI .
86
а |
б |
|
в |
|
В |
1 |
Х |
|
М=30 кН м |
|
|
3 м
F=20 кН |
|
|
|
|
3 м |
3 м |
|
|
|
|
|
|
||
А |
|
1 |
Х |
|
НА=20 кН |
||||
6 |
6Х |
|||
МА=90 кН м |
30 |
|||
|
|
|||
30 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3Х |
|
|
||||||||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3Х |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3Х |
|||
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Эпюра МР |
|
|
|
|
Эпюра М1 |
|
Эпюра МХ |
|
|
||||||||||||||||
|
|
|
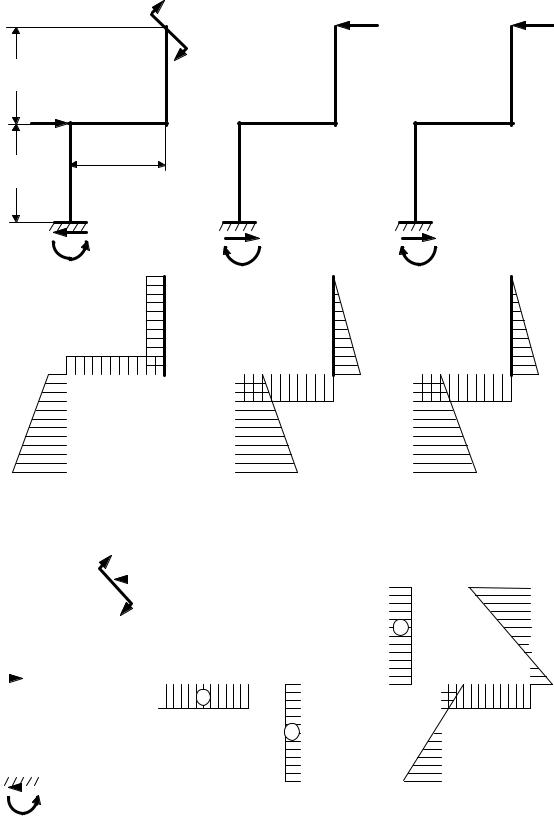
Рис. 4.42. Эпюры изгибающих моментов: а – от заданной нагрузки; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
б – от единичной силы; в – от лишней неизвестной Х |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
В Х=12,72 кН |
|
|
|
|
|
|
12,72 |
|
30 |
|
|
||||||||||||||
|
|
М=30 кН м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
F=20 кН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8,16 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8,16 |
|||
|
|
|
|
12,72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8,16 |
|||||||
|
|
|
|
А |
|
|
|
|
|
7,28 |
|
|
|
|
|
13,68 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
НА=7,28 кН |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Эпюра N |
|
|
|
|
|
|
|
Эпюра Q |
|
|
Эпюра М |
|||||||||||||||
МА=13,68 кН м |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Рис. 4.43. Окончательные эпюры внутренних усилий

87
Горизонтальное перемещение точки В от лишней неизвестной Х
δгорB |
( X ) = ∫ |
M X M1 |
dx = |
1 |
[ |
3X 3 |
2 + 3X 3 3 + |
3 |
(2 6X 6 + 2 3X 3 + |
|
|
EI |
3 |
|
6 |
||||||
|
|
EI |
|
|
|
|
||||
+6X 3+3X 6)] = 99EIX .
Подставим найденные перемещения в условие совместности деформаций и найдем значение лишней неизвестной:
−1260 +99 X = 0 , откуда X =12,72 кН.
|
|
|
|
|
|
|
Строим окончательные эпюры внутренних |
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
усилий, приложив к основной системе все на- |
||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
грузки, |
включая |
найденное |
значение |
Х |
||||||||
|
|
|
|
|
|
(рис. 4.43). Выполним проверку, перемножив |
||||||||||||
|
|
|
|
|
|
эпюру М с эпюрой М1. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
− |
30 3 |
1 + |
8,18 3 |
2 +8,18 3 3 − |
13,64 3 |
5 + |
8,18 3 |
4 = |
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
2 |
|
|
||
|
|
|
|
|
|
=147,24 – 147,3 ≈ 0. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Изогнутая ось рамы, соответствующая |
|||||||||||
|
|
|
|
|
|
эпюре |
изгибающих |
моментов |
(рис. 4.43, г), |
и |
||||||||
|
|
|
|
|
|
условиям закрепления показана на рис. 4.44. |
||||||||||||
|
|
|
|
|
|
|||||||||||||
Рис. 4.44. Изогнутая |
Крестиками на рисунке отмечены точки переги- |
|||||||||||||||||
|
|
ось рамы |
ба оси. |
|
|
|
|
|
|
|
|
|
|
|||||
88
4.4. РАСЧЕТ ПЛОСКОГО ТРУБОПРОВОДА НА ТЕМПЕРАТУРНОЕ ВОЗДЕЙСТВИЕ И ВНУТРЕННЕЕ ДАВЛЕНИЕ
Рекомендуемая литература
Камерштейн А. Г., Рождественский В. В., Ручинский М. Н. Расчет трубопроводов на прочность: Справочная книга. М.: Недра, 1969. Гл. 21, 27.
Основные определения
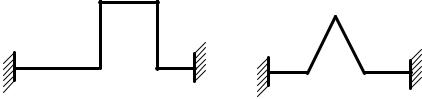
Известно, что в статически неопределимых стержневых конструкциях возникают напряжения в результате температурного воздействия. Температурные напряжения особенно велики в стержне, защемленном по двум концам (см., например, решение задачи № 4 об определении температурных напряжений [5]). Для уменьшения температурных напряжений в такого рода конструкциях (например, в трубопроводах) используются температурные компенсаторы, которые увеличивают свободу деформаций за счет изгиба. Температурные компенсаторы представляют собой статически неопределимые рамы с двумя заделками по концам (рис. 4.45). В данном разделе рассматривается расчет плоских статически неопределимых рам (плоских тру-
а б
Рис. 4.45. Температурные компенсаторы
бопроводов) на температурное воздействие по методу упругого центра. Предполагается, что стержни рамы соединены между собой жестким образом под углом 90°, все стержни имеют одинаковую жесткость.
Рассматриваемые рамы являются три раза статически неопределимыми системами. Выберем основную систему для рамы, показанной на рис. 4.45, а, отбросив левую заделку (рис. 4.46). Лишними неизвестными являются реакции в защемлении: Х1, Х2 и Х3. В точке О
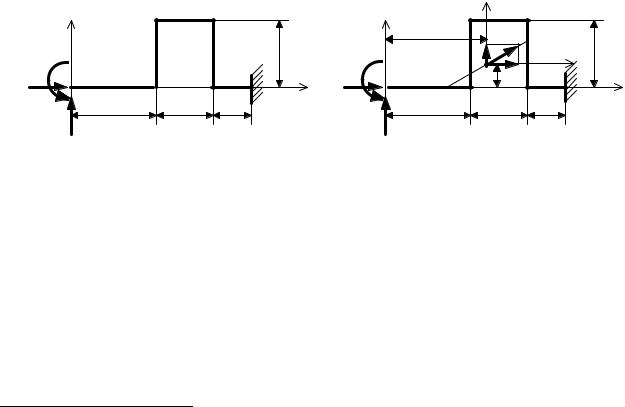
89
поместим начало декартовой системы координат хОy. Положительное направление силы Х1 должно совпадать с направлением оси х, силы Х2 – с направлением оси y. Положительное направление пары сил Х3 должно соответствовать направлению поворота оси х к оси y.13 Можно показать, что решение канонической системы уравнений метода сил для выбранной основной системы дает такие формулы для определения лишних неизвестных:
X1 = |
(I y |
C |
Lx + I x |
C |
y |
|
Ly ) |
α∆TEI ; |
(4.30) |
||||
|
|
|
|
C |
|
||||||||
|
|
|
|
|
|
|
|
2 |
|||||
|
|
I xC I yC − I xC yC |
|
|
|||||||||
X 2 = |
|
(I x |
C |
Ly + I x |
C |
y |
Lx ) |
α∆TEI ; |
(4.31) |
||||
|
|
|
|
|
|
|
C |
||||||
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
I xC I yC − I xC yC |
|
|
|||||||||
|
|
X 3 = xc X 2 − yc X1. |
(4.32) |
||||||||||
В этих формулах ∆Т – изменение температуры; α – коэффициент линейного температурного расширения; EI – жесткость стержней ра-
|
а |
|
|
|
y |
|
|
X1 |
X3 |
|
l4 |
O |
|
x |
|
|
|
||
|
l1 |
l2 |
l3 |
|
X2 |
|
|
бyc
|
y |
xc |
|
|
|
D |
xc |
l4 |
|
X3 |
|
|
|
|
|||
X1 |
|
B |
C |
yc |
|
|||
O |
|
|
|
x |
||||
|
X2 |
l1 |
A |
l2 |
|
l3 |
|
|
|
|
|
|
|
|
|
|
Рис. 4.46. К расчету трубопровода:
а– основная система;
б– точка С – упругий центр
мы; Lx, Ly – суммарные длины стержней рамы, параллельных осям х и y. При вычислении длины стержня учитывается направление обхода по длине стержня от начала координат. Если обход осуществляется по направлению оси, то длина участка рамы считается положительной, в противном случае – отрицательной. Например, для рамы, показанной на рис. 4.46, Ly = 0, так как обход левой стойки рамы от начала коор-
13 Рекомендуемое в [4] направление Х3 по ходу часовой стрелки справедливо лишь для левой системы координат, когда поворот от х к y осуществляется по часовой стрелке.
90
динат происходит по направлению оси y, а обход правой стойки – против направления оси.
Чтобы пояснить, что такое хс, yc, I xC , I yC и I xC yC , будем рассмат-
ривать раму как плоскую фигуру, состоящую из прямоугольников. Одна сторона каждого прямоугольника равна длине участка рамы, а другая сторона (толщина) всегда равна 1. Например, рама на рис. 4.46 считается плоской фигурой, состоящей из пяти прямоугольников с длинами соответственно l1, l2, l3 и 2 l4 и толщиной всех прямоугольников, равной 1. Тогда хс, yc – координаты центра тяжести этой плоской фигуры в системе координат xОy. Центр тяжести фигуры (точка С на рис. 4.46, б) называется упругим центром. Через упругий центр проведем центральные оси xc, yc, параллельные осям x, y. В формулах (4.30), (4.31) I xC , I yC и I xC yC – осевые и центробежный моменты
инерции рассматриваемой плоской фигуры относительно централь-
ных осей xc, yc.
Напомним некоторые формулы. Координаты центра тяжести плоской фигуры находим так:
xc = |
S y |
; yc = |
S |
x |
, |
(4.33) |
A |
|
|
||||
|
|
A |
|
|||
где А – площадь фигуры. В данном случае, так как толщина всех прямоугольников равна единице, площадь равна сумме длин всех участков рамы. Для рамы на рис. 4.46 A = l1 + l2 + l3 + 2 l4 ; Sx, Sy – статические моменты фигуры относительно осей x, y, которые находятся как суммы статических моментов каждого прямоугольника относительно осей x, y. Статический момент каждого прямоугольника равен произведению площади прямоугольника на координату центра тяжести прямоугольника в системе координат хОy.
Моменты инерции плоской фигуры вычисляются как суммы моментов инерции простых фигур, составляющих данную фигуру, в рассматриваемом случае момент инерции всей фигуры равен сумме моментов инерций прямоугольников единичной толщины. Для каждого прямоугольника справедливы формулы
I xпC |
= I xп0 |
+ Aпa2 ; |
(4.34) |
I пyC |
= I пy0 |
+ Aпb2 ; |
(4.35) |
