
Левченко 2 часть
.pdf71
бающий момент, вызванный этой нагрузкой (координаты x1, x2 , x3
должны отсчитываться так же, как при определении момента от заданной нагрузки):
участок 1: |
0 ≤ x1 ≤ 4 м; |
M1(x1 ) = H A x1 = 3/ 2 x1; |
|
участок 2: |
0 ≤ x2 ≤ 3м; |
M1 (x2 ) = H A 4 − RA x2 = 6 −1 x2 ;
участок 3: 0 ≤ x3 ≤ 2м;
M1(x3 ) = H B x3 = 3/ 2 x3 .
Аналогично для определения второго обобщенного перемещения – угла поворота сечения А – приложим в точке А сосредоточенную пару сил, равную единице (рис. 4.29, б), и определим изгибающий момент от этой пары:
участок 1: 0 ≤ x1 ≤ 4 м;
M 2 (x1 ) = H A x1 −1 =1/ 2 x1 −1;
участок 2: |
0 ≤ x2 ≤ 3м; |
M 2 (x2 ) = H A 4 −1 =1; |
|
участок 3: |
0 ≤ x3 ≤ 2 м; |
M 2 (x3 ) = H B x3 =1/ 2 x3.
Вариант 1. Аналитическое интегрирование формулы Максвелла – Мора
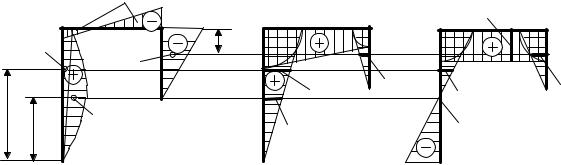
Подставим в формулу Максвелла – Мора (4.21) выражения для изгибающих моментов от заданной нагрузки, найденные ранее при определении внутренних усилий в рассматриваемой раме, умножим их на выражения для изгибающих моментов от единичных обобщенных сил на всех трех участках и выполним интегрирование. Тогда, учтя, что EI = const , проинтегрируем формулу (4.21):
|
верт. |
|
4 |
|
|
2 |
|
3 |
|
|
3 |
|
|
|
|
|
|
|
EI δ |
|
= ∫ |
(45 x |
−10 x |
|
) |
|
x dx |
+ ∫(20 − 20x |
|
)(6 − x |
|
) dx |
|
+ |
|||
|
|
|
|
|
|
|||||||||||||
2 |
B |
|
0 |
1 |
1 |
|
2 |
1 |
1 |
0 |
2 |
|
2 |
|
2 |
|
||
|
|
3 |
x3dx3 =250 кН·м3; |
|
|
|
|
|
|
|
|
|||||||
+ ∫(−35x3 ) |
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
4 |
|
|
2 |
1 |
|
|
3 |
|
|
|
|
|
|
|
|||
EI ϕA = ∫(45 |
x1 −10 x1 )( |
|
x1 |
−1)dx1 |
+ ∫(20 − 20x2 )1dx2 + |
|||
2 |
||||||||
0 |
|
|
|
|
|
0 |
||
2 |
1 |
x3dx3 =–63,3 кН·м2. |
|
|||||
+ ∫(−35x3 ) |
|
|||||||
2 |
|
|||||||
0 |
|
|
|
|
|
|
||
В соответствии с правилом знаков метода Максвелла – Мора положительный знак вертикального перемещения говорит о том, что точка В перемещается по направлению обобщенной силы, то есть вверх. Сечение А поворачивается по часовой стрелке (в сторону, противоположную направлению единичной пары сил, так как знак угла поворота отрицательный).
Вариант 2. Интегрирование формулы Максвелла – Мора с помощью правила Верещагина
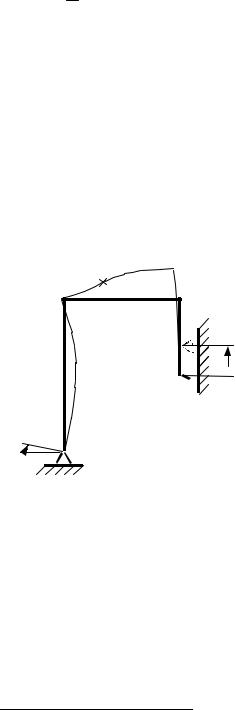
Построим эпюры моментов от заданной нагрузки М и от единичных обобщенных сил, соответствующих искомым перемещениям, М1 и М2 (рис. 4.30). Для перемножения эпюр разобьем эпюру М на 4 простые фигуры: два треугольника ω1 и ω3, сегмент ω2 и трапецию ω4. Найдем ординаты под центрами тяжести этих фигур на эпюре М1 (η1, η2 и η3 на рис. 4.30, б). Эпюру М на ригеле, имеющую форму трапеции ω4 с основаниями разного знака, умножаем на трапецию эпюры М1 по правилу трапеций (4.24). Согласно правилу Верещагина
а |
ω4 |
40 |
б |
|
|
в |
|
|
|
|
|
η′4=1 |
|
||
20 |
20 |
70 |
6 |
3 |
|
1 |
|
|
|
2/3м |
|
3 |
|
|
|
ω1 |
ω3 |
|
6 |
|
|
1 |
1 |
|
|
η1=4 |
η3=2 |
||||
|
|
|
|
η′1=1/3 |
η′3=2/3 |
||
8/3 м |
ω2 |
|
|
|
|
||
|
|
|
|
|
|
||
2 м |
|
|
η2=3 |
|
η′2=0 |
|
|
|
|
|
|
|
1 |
|
|
|
Эпюра M |
|
Эпюра M1 |
|
Эпюра M2 |
|
|
|
Рис. 4.30. Эпюры моментов: а – от заданной нагрузки; |
|
|||||
б– от единичной обобщенной силы, соответствующей δвертB . ; в – от единичной обобщенной силы, соответствующей ϕA
73
EI δверт = |
4 |
|
|
20 4 |
|
20 4 |
3 |
|
− 70 2 |
|
∑ω η |
= |
4 + |
|
3 + |
2 + |
|||||
2 |
12 |
|
2 |
|||||||
B |
k =1 |
k k |
|
|
|
|
|
|||
+ 63 (2 20 6 − 2 40 3 − 40 6 + 20 3) = 250 кН·м3.
Аналогично находим угол поворота сечения А, перемножая эпюры М и М2. Ординаты под центрами тяжести площадей ω1, ω2 и ω3 показаны на рис. 4.30, в (η′1, η′2 и η′3). Для перемножения трапеции ω4 на прямоугольник эпюры М2 нет необходимости пользоваться правилом трапеций, так как, где бы ни находился центр тяжести трапеции, значение η′4 известно (ординаты на эпюре М2 на этом участке постоянны).
EI ϕ |
|
4 |
|
′ |
20 4 |
|
1 |
|
|
= ∑ω η = |
|
|
|
+ |
|||
|
2 |
3 |
||||||
|
A |
k =1 |
k |
k |
|
|
||
δверт.
В 
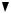 B
B
ϕA А
Рис. 4.31. Изогнутая ось рамы
20 43 |
0 + |
− 70 2 |
|
2 |
+ |
20 − 40 |
3 |
1 |
= |
|
12 |
2 |
3 |
2 |
|||||||
|
|
|
|
|
|
= −63,3 кН·м2.
Результаты, полученные по двум вариантам использования формулы Максвелла – Мора, совпадают.
В заключение построим деформированную ось рамы так, чтобы она удовлетворяла эпюре изгибающих моментов и условиям закрепления рамы (рис. 4.31). На рис. 4.31 показаны по-
лученные перемещения – δвертB . , ϕА в
соответствии с их направлениями. Точка перегиба (крестик) изогнутой оси ригеля имеет место в сечении, где меняет знак изгибающий момент. Углы рамы в процессе деформации не меняются.11
.
11 Для наглядности на изогнутой оси перемещения показаны преувеличенно большими (использован разный масштаб для изображения оси рамы и перемещений). В связи с этим на рис. 4.31 для изображения подвижной опоры применено другое обозначение.
74
4.3. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК И РАМ
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление мате-
риалов. М.: Высш. шк., 1995. Гл. 9 (§ 9.1–9.3).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 9.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 12 (§ 12.1–12.6).
Основные определения
Статически неопределимые балки и рамы – конструкции, в
которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции. Такими связями могут быть как опорные связи, так и стержни самой конструкции. Будем рассматривать балки и простые рамы, то есть такие конструкции, в которых связями, обеспечивающими геометрическую неизменяемость, являются опорные закрепления (опорные связи). Для обеспечения геометрической неизменяемости балки (рамы) в плоскости достаточно трех связей. Каждая связь запрещает какое-то перемещение. Шарнирно-подвижная опора запрещает перемещение по направлению, перпендикулярному плоскости опирания, и является одной связью. Шарнирно-неподвижная опора делает невозможными линейные перемещения по двум взаимно-перпендикулярным направлениям (вертикальному и горизонтальному) и соответствует двум связям, наложенным на конструкцию. Наконец, при наличии жесткого защемления на конце стержня становятся невозможными все перемещения: и вертикальное, и горизонтальное, и угол поворота, поэтому жесткое защемление представляет собой три связи, обеспечивающие геометрическую неизменяемость балки (рамы). Каждая дополнительная связь сверх трех для плоских систем превращает конструкцию в статически неопределимую. Такие дополнительные связи, которые не являются необходимыми для обеспечения геометрической неизменяемости конструкции, называются лишними.

75
Перед расчетом статически неопределимой конструкции необ-
ходимо сначала определить степень статической неопределимости
рассматриваемой системы. Для балок и простых рам степень статической неопределимости равна числу лишних опорных связей. В каждой связи возникает опорная реакция, поэтому степень статической неопределимости можно найти, сосчитав разность между количеством неизвестных опорных реакций и числом независимых уравнений статики. Например, балка на рис. 4.32, а является один раз статически
а |
|
б |
|
в |
|
А |
В |
А |
В |
А |
Х |
В |
|||||
|
|
wB = 0 |
Х |
|
ϕA = 0 |
Рис. 4.32. К расчету статически неопределимой балки:
а– заданная статически неопределимая балка;
б– основная система и условие совместности деформаций (вариант 1);
в– основная система и условие совместности деформаций (вариант 2)
неопределимой, так как имеет 4 связи и 4 неизвестные опорные реакции, а количество независимых уравнений равновесия – 3. В раме, показанной на рис. 4.34, а, число наложенных связей и опорных реакций в них равно 5, и эта рама является дважды статически неопределимой. Если в один из стержней балки (рамы) врезан шарнир, то количество связей уменьшается на единицу, так как становится возможным взаимный поворот сечений, примыкающих к шарниру. Появляется дополнительное уравнение для определения опорных реакций: "изгибающий момент в шарнире равен нулю" или можно сказать по-другому: "сумма моментов всех сил, расположенных слева (или справа) от шарнира, равна нулю". Так, балка с врезанным в точке Е шарниром, показанная на рис. 4.33, а, является один раз статически неопределимой: от 5 опорных связей надо вычесть одну связь, связанную с наличием дополнительного шарнира в точке Е. Из четырех оставшихся связей одна является лишней. Можно сосчитать степень статической неопределимости этой балки и иначе: для определения пяти опорных реакций можно составить четыре уравнения статики
|
|
|
|
|
|
|
76 |
|
|
а |
|
|
|
|
б |
|
|
|
|
A |
E |
B |
C |
D |
A |
E |
B |
C |
D |

 X wD = 0
X wD = 0
в X X
A |
E |
B |
C |
D |
|
|
ϕCвз. = 0 |
|
|
Рис. 4.33. К расчету статически неопределимой балки с шарниром:
а– заданная статически неопределимая балка;
б– основная система и условие совместности деформаций (вариант 1);
в– основная система и условие совместности деформаций (вариант 2)
а |
B |
б |
X1 B |
|
|
в |
|
|
|
|
|
|
|
B |
|
|
|
||
|
C |
|
|
X2 |
C |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
δгорB = 0 |
X1 А |
|
δгорA |
= 0 |
|
|
|
А |
верт |
= 0 |
X2 |
||||
|
|
|
|
δС |
|
ϕA |
= 0 |
||
|
|
|
|
|
|
|
|
||
Рис. 4.34. К расчету статически неопределимой рамы:
а– заданная статически неопределимая рама;
б– основная система и условия совместности деформаций (вариант 1);
в– основная система и условия совместности деформаций (вариант 2)
(дополнительное уравнение "изгибающий момент в шарнире Е равен нулю"). Разность между числом реакций и количеством уравнений статики равна единице, то есть балка один раз статически неопределима.
Рассмотрим один из способов расчета статически неопределимых балок и рам, а именно тот, который основан на том же принципе, что и расчет рассмотренных ранее статически неопределимых стержневых конструкций, работающих на растяжение-сжатие, кручение. Согласно этому способу для определения всех неизвестных к необходимым уравнениям равновесия добавляются уравнения совместности деформаций. При определении деформаций в уравнениях совместно-
77
сти деформаций используются физические уравнения (закон Гука). Из решения полученной системы уравнений можно найти все неизвестные реакции и определить внутренние усилия.
Для уменьшения в системе уравнений количества неизвестных, которые определяются в первую очередь, при расчете балок и рам чаще всего используют прием, связанный с выбором основной системы. Основная система – это статически определимая конструкция, полученная из заданной системы путем отбрасывания лишних связей. Реакции в отброшенных связях принято называть лишними неизвестными и обозначать Хi. Решение задачи (раскрытие статической неопределимости) сводится сначала к определению лишних неизвестных. Для их нахождения используются уравнения совместности деформаций – это условия кинематической эквивалентности основной и заданной систем, то есть равенства, приравнивающие нулю деформации по направлению отброшенных в основной системе связей. Количество уравнений совместности деформаций равно степени статической неопределимости. Зная величины лишних неизвестных, можно найти из уравнений равновесия остальные реакции. Обсудим подробно, как выбирать основную систему и записывать уравнения совместности деформаций.
На рис. 4.32, б, в – 4.34, б, в показаны по два варианта основных систем, выбранных для заданных систем, изображенных на рис. 4.32, а – 4.34, а. Балка на рис. 4.32, а один раз статически неопределима, для выбора основной системы необходимо отбросить одну связь. В первом варианте основной системы, изображенном на рис. 4.32, б, отброшена подвижная опора в точке В. Вертикальная реакция в отброшенной связи (лишняя неизвестная) обозначена буквой Х. Условие совместности деформаций для этого варианта основной системы: wB = 0 – это условие, приравнивающее нулю вертикальное
перемещение (прогиб) в точке В балки, так как в заданной системе этот прогиб был невозможен. Во втором варианте на рис. 4.32, в жесткое защемление заменено шарнирно-неподвижной опорой. Лишней неизвестной является реактивный момент. Поскольку в точке А стал возможным поворот сечения, то условие совместности деформаций полагает этот угол поворота равным нулю: ϕA = 0.
78
Для выбора основной системы в дважды статически неопределимой раме на рис. 4.34, а требуется отбросить две связи. На рис. 4.34, б, в лишние неизвестные обозначены Х1 и Х2. В основной системе, показанной на рис. 4.34, б, стали возможны по сравнению с
заданной системой горизонтальное перемещение в точке В – δгорB и вертикальное перемещение в точке С – δCверт , поэтому эти перемеще-
ния необходимо приравнять нулю. Это и есть условия совместности деформаций для варианта основной системы, показанной на рис. 4.34, б:
δгорB = 0; δCверт = 0. |
(4.26) |
Аналогично для основной системы, изображенной на рис. 4.34, в, условия совместности деформаций следующие: δгорA = 0; ϕA = 0.
Обсудим еще вариант 2 основной системы, показанный на рис. 4.33, в. В точке С сделан разрез стержня и между соседними сечениями вставлен шарнир. Лишней неизвестной в этом случае является изгибающий момент, возникающий в сечении С при отсутствии шарнира. Этот изгибающий момент изображен на рис. 4.33, в в виде двух одинаковых пар сил Х. Чтобы записать уравнение совместности деформаций, надо понять, чем отличается деформация заданной системы от деформации рассматриваемой основной системы. В заданной системе поворот соседних сечений, расположенных бесконечно близко слева и справа от точки С, возможен на один и тот же угол (сечения "склеены"). После разреза и добавления шарнира соседние сечения
могут поворачиваться относительно друг друга на угол |
ϕCвз |
ϕCвз
Рис. 4.35. Взаимный угол поворота сечений
около шарнира
(рис. 4.35). Этот взаимный угол поворота соседних сечений в точке С мы и должны положить равным нулю при записи условия совместности деформаций: ϕCвз = 0.
Для определения лишних неизвестных необходимо найти деформации в условиях совместности деформаций любым способом. Как правило, деформации находят методом Максвелла – Мора с использованием правила Верещагина.

79
Удобно искать деформации отдельно от заданной нагрузки δ(P) и от лишних неизвестных δ( X i ) . Например, условия совместности деформаций (4.26) можно записать так:
δгорB |
= δгорB (P) + δгорB ( X1) + δгорB ( X 2 ) = 0 ; |
(4.27) |
δCверт |
= δCверт (P) + δCверт ( X1) + δCверт ( X 2 ) = 0 . |
(4.28) |
Таким образом, для дважды статически неопределимой системы получаем систему уравнений из двух уравнений с двумя неизвестными, из которых и находим лишние неизвестные. После определения X1 и X 2 находим остальные неизвестные реакции и строим оконча-
тельные эпюры внутренних усилий N, Q и М, используя уравнения статики.
Окончательную эпюру изгибающих моментов для один раз статически неопределимой системы можно проверить, перемножив ее с эпюрой моментов от единичной силы12. Результатом этого перемножения должен быть ноль, то есть
∫ |
EI |
|
|
|
M M1 |
dx = 0 . |
(4.29) |
|
|
||
Условие (4.29) – это условие совместности деформаций, подтверждающее равенство нулю деформаций по направлению лишней неизвестной.
12 Если конструкция два раза статически неопределима, то результат перемножений эпюры М и эпюр М1 и М2 должен равняться нулю.

80
Примеры решения задач
4.3.1. Расчет статически неопределимой балки (задача № 23)
Условие задачи |
|
|
|
|
|
|
|
||||
|
|
|
|
|
Балка, показанная на рис. 4.36, с шар- |
||||||
М |
|
|
|
|
ниром в точке Е загружена сосредоточен- |
||||||
|
|
|
|
ной парой М. Требуется определить |
внут- |
||||||
A |
E |
B |
C |
D |
|||||||
ренние усилия и построить изогнутую ось |
|||||||||||
а |
|
а |
а |
а |
балки. |
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Рис. 4.36. Заданная балка |
Как было показано выше, заданная |
||||||||||
балка является один раз статически неопре- |
|||||||||||
|
|
|
|
|
делимой. Выберем основную систему, от- |
||||||
бросив одну лишнюю связь, например, подвижную опору в точке D |
|||||||||||
(рис. 4.37). Опорную реакцию в точке D бу- |
М |
|
|
|
|
||||||
дем считать лишней неизвестной и обозна- |
A |
E |
B |
C |
D |
||||||
чим буквой Х. Уравнением для определения |
|||||||||||
|
|
|
|
|
|||||||
лишней |
неизвестной |
является уравнение |
|
|
|
|
Х |
||||
совместности деформаций. Для выбранной |
a |
|
a |
a |
a |
||||||
основной системы это условие, приравни- |
|
|
|
|
|
||||||
вающее |
нулю |
прогиб балки в точке D: |
Рис. 4.37. Основная |
||||||||
wD = 0. Прогиб в точке D можно найти как |
|||||||||||
|
|
система |
|
||||||||
сумму прогиба, вызванного заданной на- |
|
|
|
|
|
||||||
грузкой (парой сил М) и прогиба от лишней неизвестной Х, т. е. усло- |
|||||||||||
вие совместности деформаций можно записать так: |
|
|
|
|
|||||||
|
|
|
|
|
wD = wD (M ) + wD ( X ) = 0 . |
|
|
|
|
||
Будем искать прогиб методом Максвелла – Мора с использова- |
|||||||||||
нием правила Верещагина. Сначала найдем wD (M ) . Для этого по- |
|||||||||||
строим в основной системе эпюры изгибающего момента от заданной |
|||||||||||
нагрузки (пары М в данной задаче) – ММ и изгибающего момента от |
|||||||||||
единичной обобщенной силы, соответствующей искомому перемеще- |
|||||||||||
нию, – М1. Чтобы построить эпюру ММ, найдем опорные реакции. Го- |
|||||||||||
