
Левченко 2 часть
.pdf
21
Пример 2
Условие задачи
На балку кроме равномерно распределенной нагрузки действует линейно распределенная (треугольная) нагрузка (рис. 4.7, а). Построим эпюры распределения поперечной силы и изгибающего момента, обращая внимание на определение Q и М на участке с треугольной нагрузкой.
Решение
Найдем опорные реакции. Балка имеет шарнирное опирание и для определения двух не равных нулю опорных реакций RA и RB (горизонтальная реакция HA = 0) составим два независимых уравнения статики. Рациональными уравнениями, в каждое из которых входит одна неизвестная реакция, в данном случае являются:
ab 2
∑mA = 0; q1a 2 + q2 2 3 b − Fb − M + RB (b + c) = 0 ,
∑mB = 0; q1a(a2 + b + c) − q2 b2 (b3 + c) + Fc − M − RA(b + c) = 0.
Напомним как определяется момент от треугольной нагрузки.
Равнодействующая от треугольной нагрузки равна площади треугольника q2 b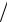 2 и приложена в центре тяжести треугольника, по-
2 и приложена в центре тяжести треугольника, по-
этому плечо этой равнодействующей относительно точки А равно (2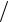 3) b , а относительно точки В – (b
3) b , а относительно точки В – (b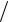 3) + c . Из этих уравнений най-
3) + c . Из этих уравнений най-
дем RA = – 31,9 кН, RB = – 18,1 кН. Отрицательные знаки показывают, что обе реакции направлены не вверх, как показано на рис. 4.7, а, а в противоположную сторону. Для проверки опорных реакций составим уравнение равновесия "сумма проекций сил на вертикальную ось z равна нулю":
∑z = 0; 10 1 −40 4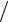 2 +20 +31,9 +18,1 = 80 −80 = 0 .
2 +20 +31,9 +18,1 = 80 −80 = 0 .
Определение внутренних усилий производим, записывая выражения для Q и М в таблицу (табл. 2).
Поясним выражения для Q и М на втором участке, а именно третьи слагаемые в этих выражениях, учитывающие треугольную нагрузку. Чтобы найти равнодействующую от треугольной нагрузки,

22
расположенной слева от рассматриваемого сечения на участке длиной х2, определим интенсивность распределенной нагрузки в сечении х2, которая на рис. 4.7, а обозначена qx . Для этого составим пропорцию:
qx q2 = x2 b , откуда qx = 404x2 . Тогда равнодействующая этой рас-
пределенной нагрузки на участке длиной х2 qx x22 = 404x2 x22 . Она приложена в центре тяжести треугольника, и изгибающий момент,
создаваемый этой нагрузкой, равен |
40 x22 |
|
x2 |
|
, где |
|
x2 |
– плечо равно- |
|||||||||||||
|
|
|
|
3 |
|||||||||||||||||
действующей. |
|
|
|
8 |
|
|
|
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пределы |
Выражения для Q и М |
|
|
|
|
|
|
|
|
Граничные значения |
|||||||||||
|
|
|
|
|
|
|
|
Q, кН |
М, кН м |
||||||||||||
измене- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния хна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вна- |
|
|
в |
вна- |
в |
участке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чале |
|
конце |
чале |
конце |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
участка |
|
участка |
участка |
участка |
|
Участок1 |
Q(x1 ) = −10x1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
– 10 |
0 |
– 5 |
||
0 ≤ x1 ≤1 |
M (x1 ) = −10x1 x1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Участок2 |
Q(x2 ) = −10 − 31,9 + 40 |
x2 |
|
x2 |
|
; |
|
|
|
|
|
|
|
|
– 41,9 |
|
38,1 |
– 5 |
– 66,1 |
||
0 ≤ x2 ≤ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
2 |
|
|
x |
2 |
|
x |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
M (x2 ) = −10(0,5 + x2 ) − 31,9x2 |
+ 40 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
8 |
|
3 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Участок3 |
Q(x3 ) = 18,1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
18,1 |
|
18,1 |
– 30 |
– 66,1 |
||
0 ≤ x3 ≤ 2 |
M (x3 ) = −30 − 18,1 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку поперечная сила на втором участке меняет знак, найдем экстремальное значение изгибающего момента в сечении х0 на этом участке (рис. 4.7, б). Определим величину х0, приравняв выражение для поперечной силы на втором участке нулю:
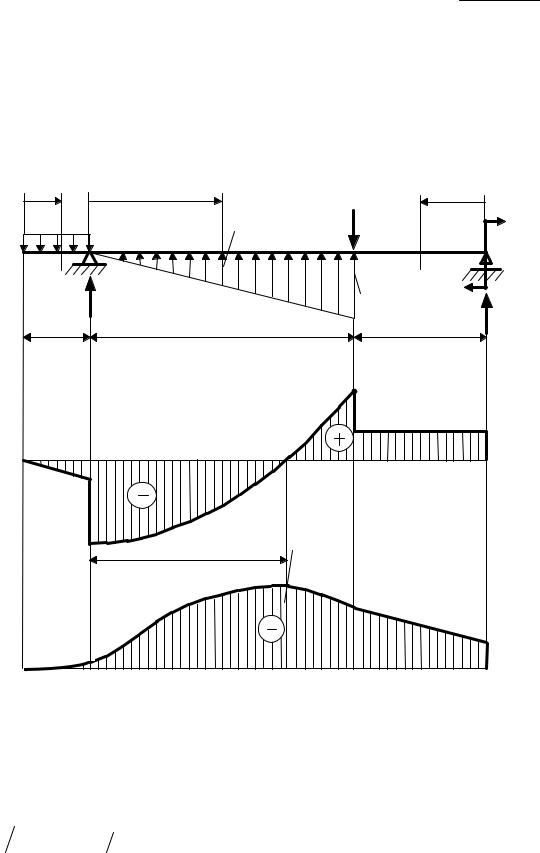
Q(x0 ) = −41,9 + |
40x02 |
= 0 , откуда х0 = 2,89 м. Тогда |
|
8 |
|||
|
|
23
M max = M (x2 = x0 ) = −10(0,5 + 2,89) − 31,9 2,89 + 40 242,893 = = 86,0кН·м
По полученным в таблице выражениям строим эпюры внутренних усилий. Напомним, что выпуклость эпюры М направлена в сторону распределенной нагрузки. Выпуклость эпюры Q на втором уча-
а |
|
|
|
|
x1 |
x2 |
F=20 кН |
x3 |
M = 30 кН м |
q1 = 10 кН/м |
|
|
||
qx |
|
|
||
|
A |
|
B |
|
|
|
|
||
|
|
|
|
|
|
RA = –31,9 кН |
q2 = 40 кН/м |
RB = –18,1 кН |
|
a=1 м |
b=4 м |
c=2 м |
|
|
|
|
|||
б |
|
38,1 |
|
|
|
|
|
|
18,1 |
Эпюра Q
10
41,9 |
x0=2,89 м |
Mmax = 86,0 |
66,1
30
5
Эпюра M
Рис. 4.7. К решению примера 2 по построению эпюр Q и М:
а– схема балки с нагрузками;
б– эпюры поперечной силы и изгибающего момента
стке |
можно определить по знаку второй |
производной |
d 2Q |
dx2 = −dq dx . В данном случае функция q(x) |
является убы- |
24
вающей, следовательно dq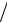 dx < 0 , а d 2Q
dx < 0 , а d 2Q dx2 > 0 . Это означает, что
dx2 > 0 . Это означает, что
эпюра Q имеет выпуклость вниз. Можно определить выпуклость эпюры поперечной силы и по-другому. В сечении, где интенсивность распределенной нагрузки равна нулю (начало второго участка в данной задаче), угол наклона касательной к кривой Q(x) должен равняться нулю, так как в этом сечении dQ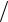 dx = 0. Это возможно тогда, когда
dx = 0. Это возможно тогда, когда
функция Q(x) имеет выпуклость вниз.
После того, как Вы нарисовали эпюры, рекомендуем обязательно проанализировать их по правилам проверки правильности построения эпюр.
4.1.2. Проверка прочности балок при плоском поперечном изгибе (задачи № 16–19)
Рекомендуемая литература:
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление мате-
риалов. М.: Высш. шк., 1995. Гл. 6 (§ 6.1–6.3), гл. 7 (§ 7.1, 7.2), гл. 4 (§ 4.1, 4.2).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 5 (§ 23–24), гл. 15.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 7 (§ 7.6–7.8, 7.10), гл. 5 (§ 5.1–5.5).
Если Вы научились строить эпюры Q и М, то можете приступать к проверке прочности балок. Задача о проверке прочности балки чаще всего сводится к решению двух вопросов:
•подбору сечения балки, т. е. определению таких минимальных размеров поперечного сечения, которые удовлетворяют условиям прочности в опасных точках;
•определению грузоподъемности балки, т. е. нахождению такой максимальной нагрузки (допускаемой нагрузки) на балку, при которой удовлетворяются условия прочности во всех опасных точках.
Рассмотрим примеры проверки прочности балок круглого или прямоугольного сечений, двутавровых балок и балок произвольного моносимметричного сечения.
25
Пример 1
Условие задачи
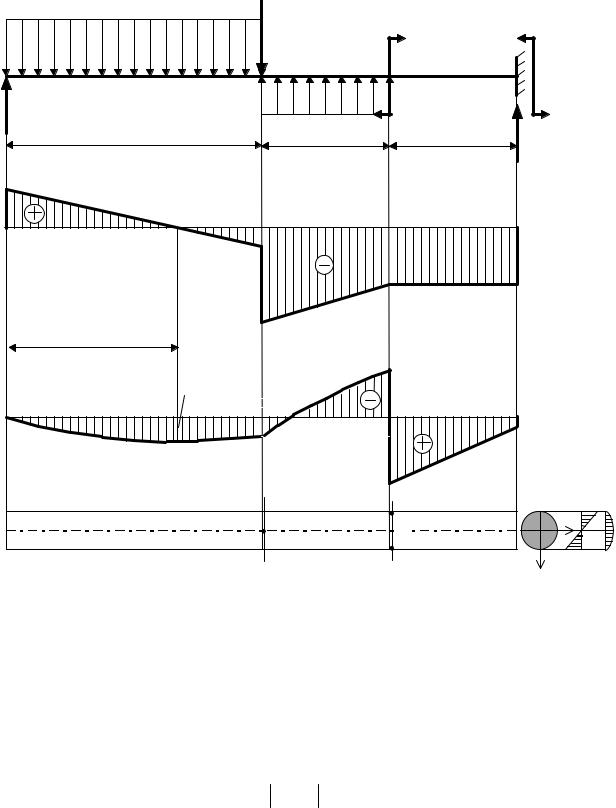
На балку круглого поперечного сечения действует нагрузка, показанная на рис. 4.8, а. Требуется подобрать размеры поперечного сечения (или определить грузоподъемность балки) так, чтобы выполнялись условия прочности во всех опасных точках.
Решение
Строим эпюры Q и М (рис. 4.8, б). Эпюры Q и М нужны для того, чтобы найти положение опасных сечений и опасных точек в балке. Найдем положение опасных сечений для этой балки. Опасными сечениями в балках круглого и прямоугольного сечений являются:
•сечение, где действует максимальный по модулю изгибающий момент (сечение а–а на рис. 4.8, в);
•сечение, где действует наибольшая по абсолютной величине поперечная сила (сечение b–b на рис. 4.8, в).
В опасных сечениях находятся опасные точки – точки, в которых действуют либо максимальные нормальные, либо максимальные касательные напряжения. Чтобы найти положение опасных точек, по-
смотрим на эпюры распределения нормальных σ и касательных τ напряжений по высоте балки, которые построены на рис. 4.8, в. Из эпюры σ видно, что наибольшие нормальные напряжения действуют в точках, наиболее удаленных от нейтральной оси y. Таким образом, опасными точками с максимальными нормальными напряжениями являются точки 1, 1′, расположенные в сечении а–а (рис. 4.8, в). В одной точке действуют максимальные растягивающие напряжения, в другой – максимальные сжимающие. В данной задаче в сечении а–а максимальный момент положителен, т. е. он изгибает балку выпуклостью вниз, поэтому в точке 1 действуют растягивающие, а в точке 1′ – сжимающие напряжения. Если допускаемые напряжения при растяжении и сжатии материала балки одинаковы (дерево или пластичный материал), то обе точки являются равноопасными. Опасная точка с максимальными касательными напряжениями, как видно из эпюры τ, расположена на оси балки в сечении b–b, где действует наибольшая поперечная сила (точка 2 на рис. 4.8, в).
|
|
26 |
|
|
|
а |
|
|
|
|
|
q1=15 кН/м |
=30 кН |
|
МА=5 кН м |
||
|
F2 |
||||
|
|
М= 60 кН м |
|
|
|
|
|
|
|
А |
|
F1=20 кН |
q2=10 кН/м |
|
|
|
|
|
b=1 м |
|
|
|
|
a=2 м |
|
c=1 м |
RA=30 кН |
||
б |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
Эпюра Q |
|
|
10 |
|
|
30 |
|
|
|
|
|
|
|
x0=1,33 м |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
Mmax=13,3 |
|
|
Эпюра М |
|
|
|
|
|
||
|
10 |
|
|
5 |
|
|
|
35 |
|
|
|
в |
|
|
|
|
|
b |
|
a |
|
|
|
|
|
|
|
||
|
2 |
|
1′ |
|
y |
|
|
|
1 |
|
|
|
b |
|
a |
z |
Эп.σ Эп.τ |
Рис. 4.8. К решению примера 1 о проверке прочности балки: |
|||||
а – схема балки с нагрузками; б – эпюры внутренних усилий; |
|||||
|
в – опасные сечения и опасные точки |
|
|
||
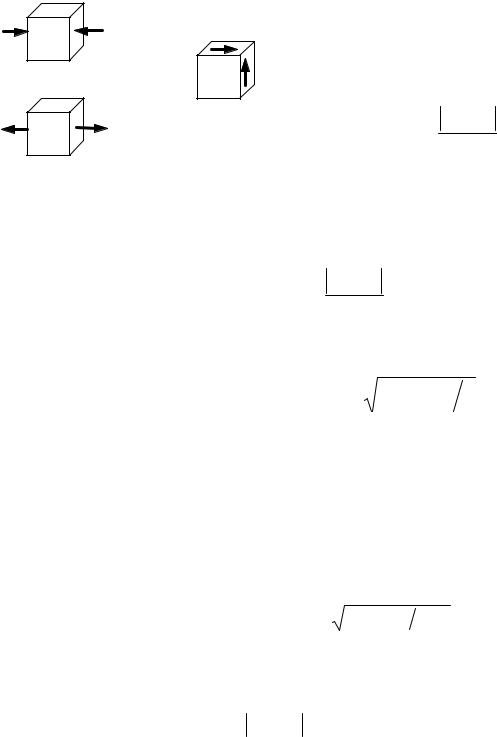
Запишем условия прочности в опасных точках. Начнем с рассмотрения опасных точек 1, 1′, так как именно эти точки чаще всего бывают наиболее опасными. Эти точки находятся в линейном напряженном состоянии (рис. 4.9, а) и условие прочности в этих точках записывается так же, как при растяжении-сжатии:
σmax ≤[σ],
27
a |
σmax |
б |
|
1′ |
τmax |
|
|
|
|
|
2 |
σmax
1
Рис. 4.9. Напряженное состояние опасных точек
Wyнеобх ≥
где максимальные напряжения определяем по формуле (4.3). Тогда условие прочности в точках 1, 1′ будет иметь вид
M max ≤[σ].
Wy
Если стоит задача под-
бора сечения, то из этого условия находим требуемый момент сопротивления балки:
M max ,
[σ]
а, зная момент сопротивления, по формулам (4.5) определяем размеры поперечного сечения балки. Например, для балки круглого попе-
речного сечения необходимый радиус r ≥ 3 4Wyнеобх π. Для деревян-
ных балок диаметр ходовых бревен ограничен и не должен быть больше 26 см. Для бревна с радиусом 13 см момент сопротивления равен 1725 см3 . Если полученное из условия прочности значение необходимого момента сопротивления будет больше 1725 см3, то следует подобрать сечение из нескольких бревен. В рассматриваемом примере для деревянной балки с [σ] = 10 МПа = 1кН/см2 найдем Wyнеобх ≥ 4000 см3. Тогда количество бревен 4000/1725 = 2,32 ≈ 3. И
радиус одного из трех бревен будет r ≥ 3 4 4000 3 π= 11,9 ≈ 12 см. Если требуется определить грузоподъемность балки, то из
условия прочности в точках 1, 1′ находим максимальное значение изгибающего момента:
M max ≤Wy [σ],
которое зависит от нагрузки. Зная эту зависимость из эпюры М, найдем значение допускаемой нагрузки.
Решение задачи будет закончено только тогда, когда мы убедимся, что полученный размер поперечного сечения балки (или найденная допускаемая нагрузка) удовлетворяют условию прочности во второй опасной точке. Поскольку в точке 2 действуют только касатель-

28
ные напряжения (нормальные напряжения в точках, лежащих на оси балки, равны нулю – это видно из эпюры σ на рис 4.8, в), то напряженное состояние этой точки – чистый сдвиг (рис. 4.9, б). Если неизвестно опытное значение допускаемого касательного напряжения, то условие прочности при чистом сдвиге записывается по соответствующей материалу балки теории прочности. Например, для пластичного материала из формул (4.9), (4.10) для чистого сдвига можно записать такие условия прочности для точки 2:
τmax ≤[σ]2 – по третьей теории и
τmax ≤[σ] |
3 |
– по четвертой теории прочности. |
|
|
Для деревянной балки, а дерево – анизотропный материал, теории прочности, полученные для изотропных материалов, не справедливы. В этом случае для проверки прочности необходимо знать допускаемое значение касательного напряжения [τ], полученное на основании опытных данных. Тогда для деревянной балки условие прочности в точке 2 записывается так:
τmax ≤[τ].
Здесь максимальное касательное напряжение τmax определяем в зави-
симости от формы поперечного сечения по формулам (4.6). Например, для рассматриваемой балки с подобранным сечением из трех бревен радиусом 12 см
τmax |
|
= |
|
4 40 |
= 0,039 кН/см2, |
|
|
||||
|
3 π 122 |
||||
|
|
3 |
|
||
что меньше [τ] = 2 МПа = 0,2 кН/см2.
Если условие прочности в точке 2 выполняться не будет, то необходимо подобрать сечение или найти грузоподъемность балки из условия прочности в этой точке.
Пример 2
Условие задачи
Стальная прокатная двутавровая балка загружена нагрузками, показанными на рис. 4.10, а. Подберем номер двутавра так, чтобы выполнялись условия прочности во всех опасных точках.

29
Решение
Строим эпюры Q и М. По построенным эпюрам Q и М (рис. 4.10, б) найдем положение опасных точек в двутавровой балке. Сначала покажем на фасаде балки опасные сечения. Кроме опасных сечений, где действуют максимальный изгибающий момент (сечение а–а на рис. 4.10, в) и наибольшая поперечная сила (сечение b–b на рис. 4.10, в), в двутавровой балке существует еще одно опасное сечение – это сечение, где Q и М одновременно имеют большие значения. В рассматриваемом примере это сечение с–с на рис. 4.10, в. В опасных сечениях находятся опасные точки. В сечении а–а – точки 1, 1′ с максимальными нормальными напряжениями, в сечении b–b – точка 2, в которой действует наибольшее касательное напряжение. Особенностью проверки прочности двутавровой балки является появление новых по сравнению с балками круглого и прямоугольного сечений опасных точек. Это связано с особенностью эпюры распределения касательных напряжений по высоте двутавра. Точки 3, 3′, находящиеся в сечении с–с и расположенные в крайних точках стенки на сопряжении с полкой (рис. 4.10, в), опасны, так как в них одновременно действуют большие нормальные и большие касательные напряжения.
Подберем размер двутавра (номер двутавра) из условия прочности в точках 1, 1′ – именно эти точки являются, как правило, наиболее опасными, а затем проверим прочность в остальных опасных точках. Точки 1, 1′ находятся в линейном напряженном состоянии (рис. 4.9, а) и условие прочности в этих точках имеет вид
M max ≤[σ].
Wy

30
Отсюда определяем необходимый момент сопротивления Wyнеобх . По таблице сортамента прокатной стали (например, в [1])
подбираем номер двутавра, у которого момент сопротивления Wy имеет близкое к Wyнеобх значение. (Обратите внимание, что в таблице сортамента – другое обозначение осей и принятому нами обозначе-
а |
|
|
|
|
|
q1 |
= 10 кН/м |
|
|
F = 20 кН |
M = 30 кН м |
|
|
|
|||
|
A |
|
|
|
B |
|
|
|
|
|
|
|
RA = –31,9 кН |
|
q2=40 кН/м |
RB = – 18,1 кН |
|
|
a=1 м |
b=4 м |
|
c=2 м |
|
б |
|
|
|
38,1 |
|
|
|
|
|
|
18,1 |
|
|
|
|
|
Эпюра Q |
|
10 |
|
|
|
|
|
41,9 |
x0=2,90 |
Mmax = 86,0 |
|
|
|
|
|
|
||
|
|
|
|
66,1 |
|
|
5 |
|
|
|
30 |
|
|
|
|
Эпюра M |
|
в |
|
|
|
|
|
b |
|
a |
c |
|
|
|
|
|
|||
|
2 |
|
1 |
3 |
|
|
|
|
y |
||
|
|
|
1′ |
3′ |
|
|
|
|
|
||
|
b |
|
a |
c |
z Эп.σ Эп.τ |
Рис. 4.10. К решению примера 2 о проверке прочности двутавровой балки:
а– схема балки с нагрузками; б – эпюры внутренних усилий;
в– опасные сечения и опасные точки
