
Левченко 2 часть
.pdf
61
25 |
ω2 |
25 1/3 b |
2/3 b |
ω5 |
|
|
|
|
|
= |
|
+ |
|
+ |
10 |
2/3 b |
1/3 b 10 |
ω3 |
1/2 b 1/2 b |
b = 1 м |
|
|
|
|
Рис. 4.24. Разбивка эпюры М на втором участке на три площади
ω6 . Независимо от положения центра тяжести трапеции (а оно не оп-
ределено) ордината под центром тяжести равна единице, так как изгибающий момент М1 на участке перемножения является постоянной величиной, всюду равной единице. То есть η6 =1. Поскольку на всех
остальных участках |
|
изгибающий |
момент М1 = 0 и |
||||||
η1 = η2 = η3 = η4 = η5 = 0, то по формуле (4.22) искомое перемеще- |
|||||||||
ние |
|
|
|
|
|
|
|
20 кН м2 |
|
δ = ϕ |
B |
= |
1 |
ω |
η = |
1 |
20 1 = |
. |
|
EI |
EI |
|
|||||||
1 |
|
|
6 6 |
|
EI |
||||
Полученная величина угла поворота совпадает с найденной ранее аналитическим методом. Положительный знак говорит о том, что поворот сечения В происходит по направлению обобщенной силы, то есть в соответствии с принятым на рис. 4.23, б направлением единичной пары по часовой стрелке. Теперь будем искать прогиб сечения С. Загрузим балку новой обобщенной силой, соответствующей прогибу в точке С. Такой обобщенной силой будет сосредоточенная сила, равная единице и приложенная в точке С. Эпюра изгибающих моментов М2 от этой единичной силы показана на рис. 4.23, в. Согласно формуле (4.22) искомый прогиб
|
|
= w |
|
1 |
6 |
|
η′ . |
δ |
|
= |
∑ω |
||||
|
|
||||||
|
2 |
C |
|
EI k=1 |
k |
k |
|
Найдем ординаты на эпюре М2, расположенные под центрами тяжести шести фигур, на которые разбита эпюра М. Положение центров тяжестей всех фигур, кроме ω6 , показано на рис. 4.23, а. Орди-
нату на эпюре М2, расположенную под центром тяжести какой-то фи-

62
гуры, можно найти либо из подобия треугольников, либо как изгибающий момент от единичной силы под центром тяжести рассматриваемой фигуры. Используем второй вариант вычисления ординат. Изгибающий момент под центром тяжести треугольника ω1 равен зна-
чению силы (1), расположенной слева от сечения, умноженной на плечо ( 4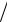 3 м), со знаком минус. То есть
3 м), со знаком минус. То есть
η1′ = − 43 м.
Аналогично ордината под центром тяжести треугольника ω2
равна силе (1), умноженной на плечо (2 +2/3 = 8/3 м), со знаком минус. И так же для остальных фигур, положение центров тяжести которых известно:
′ |
= − |
8 |
м, |
′ |
= − |
7 |
|
м, |
′ |
= −1м, |
′ |
= −2,5м. |
|
|
|
|
|
||||||||||
η2 |
3 |
η3 |
3 |
η4 |
η5 |
||||||||
|
|
|
|
|
|
|
|
|
|
||||
Поскольку положение центра тяжести трапеции ω6 не опреде-
лено и невозможно в этом случае найти ординату под центром тяжести, воспользуемся на этом участке формулой перемножения трапе-
ций (4.24):
ω6η′6 = 16 [2 35 (−3) +2 5 (−4) +35 (−4) +5 (−3)]= −67,5 кН·м3.
Искомое перемещение – прогиб в точке С
δ |
2 |
= w |
= |
1 |
[10(− |
4 |
) + (−12,5)(− |
8 |
) +5(− |
7 |
) +10(−1) + (− |
5 |
)(−2,5) − |
||
|
|
|
|
|
|
||||||||||
|
C |
|
|
EI |
3 |
|
3 |
3 |
6 |
|
|||||
|
|
|
|
|
|
|
|||||||||
− 67,5] = − |
|
67,1 кН м3 |
. |
|
|
|
|
|
|
||||||
|
|
EI |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Результат совпадает с найденным ранее прогибом в точке С аналитическим способом. Отрицательный знак перемещения показывает, что точка С перемещается в сторону, противоположную выбранному направлению единичной силы (см. рис. 4.23, в), то есть вверх.
Пример 2
Условие задачи
Определим угол поворота сечения А и прогиб сечения D в балке, показанной на рис. 4.21, а, методом Максвелла – Мора с использова-

63
нием правила Верещагина (перемножением эпюр). Ранее эти перемещения были найдены аналитическим методом, сравним результаты, полученные двумя способами.
Решение
Построим эпюры изгибающих моментов от заданной нагрузки (рис. 4.25, а) и от единичных обобщенных сил, соответствующих искомым перемещениям (рис. 4.25, б, в). Разобьем эпюру моментов от заданной нагрузки на три треугольника и найдем их площади:
ω = |
40 4 |
= 80кН·м2; |
ω |
2 |
= |
−20 4 |
= −40 кН·м2; |
||
|
|
||||||||
1 |
2 |
|
|
|
|
2 |
|
||
|
|
−20 1 |
|
|
|
|
|||
|
|
ω = |
|
= −10кН·м2. |
|
||||
|
|
|
|
||||||
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения угла поворота сечения А перемножим эпюры М и М1. Для этого найдем ординаты на эпюре М1, расположенные под центрами тяжести треугольников:
|
|
|
η = |
2 |
; |
η |
2 |
= |
|
1 |
; η = 0. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
3 |
|
|
|
3 |
3 |
|
|
|
|
|
|
|||
Тогда угол поворота сечения А согласно формуле (4.22) |
|
|
|||||||||||||||||
ϕA = |
1 |
∫M M1dx = |
1 |
|
(ω1η1 |
+ ω2η2 |
+ ω3η3 ) = |
1 |
(80 |
2 |
−40 |
1 |
) = |
||||||
EI |
EI |
|
EI |
3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||
= 40 кН м2 .
EI
Положительный знак угла поворота показывает, что поворот сечения А происходит по направлению обобщенной силы, то есть в соответствии с показанной на рис. 4.25, б единичной парой сил по ходу часовой стрелки. Результат совпадает с полученным ранее аналитическим способом.
|
|
|
|
64 |
|
|
а |
|
|
|
|
|
F=20кН |
A |
B |
M=40 кН.м |
|
C |
D |
|
|
|
|
||||
|
1 м RB=15кН 4 м RC=35кН 1 м |
|||||
|
|
4/3 м |
ω2 |
|
20 ω3 |
|
|
|
|
|
|||
|
|
|
|
|
|
Эпюра М |
б |
40 |
|
|
4/3 м |
2/3 м |
|
1 |
|
ω1 |
||||
|
|
|
|
|
||
|
|
1/4 |
η1 |
η2 |
1/4 |
Эпюра М1 |
|
|
|
||||
1 |
|
|
|
|
|
1 |
в |
|
|
|
|
|
|
|
|
1/4 |
|
η′2 |
5/4 |
|
|
|
|
η′1 |
η′3 |
||
|
|
|
|
1 |
||
|
|
|
|
|
|
Эпюра М2 |
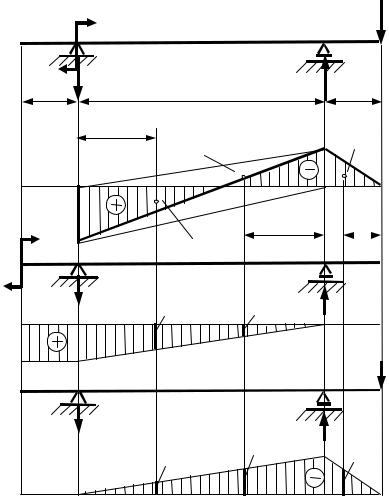
Рис. 4.25. Эпюры моментов: а – от заданной нагрузки; б – от единичной обобщенной силы, соответствующей углу поворота сечения А;
в – от единичной обобщенной силы, соответствующей прогибу в точке D
Чтобы найти прогиб сечения D, используем при перемножении эпюру М2. Ординаты на эпюре М2 под центрами тяжести треугольников будут такими:
|
η1′ = − |
|
1 |
|
м; η′2 |
= − |
2 |
м; |
η′3 |
= − |
2 |
м. |
|||
|
3 |
|
3 |
||||||||||||
|
|
|
|
|
3 |
|
|
|
|
||||||
Найдем прогиб сечения D по формуле (4.22): |
|
|
|||||||||||||
wD = |
1 |
∫M |
M2dx = |
1 |
|
|
|
′ |
′ |
|
|
′ |
|||
|
|
|
|
|
|
|
|||||||||
EI |
EI |
|
(ω1η1 + ω2 |
η2 |
+ ω3η3 ) = |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
65 |
|
||
= |
1 |
(−80 |
1 |
+ 40 |
|
2 |
+10 |
|
2 |
) = |
6,67 кН м3 |
. |
|
EI |
3 |
3 |
3 |
EI |
|||||||||
|
|
|
|
|
|
|
|
||||||
Прогиб сечения D получился положительным. Это означает, что точка D перемещается по направлению единичной силы. Поскольку единичная сила показана на рис. 4.25, в направленной вниз, то и перемещение точки D происходит вниз. Полученный результат совпадает с тем, который был получен ранее аналитическим способом.
66
4.2. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ РАМ
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление мате-
риалов. М.: Высш. шк., 1995. Гл. 2 (§ 2.6), гл. 8 (§ 8.9).
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 11 (§ 11.4, 11.5).
Основные определения
Статически определимая рама – конструкция, состоящая из нескольких изгибаемых стержней, закрепленных так, что опорные реакции и внутренние усилия можно найти с помощью уравнений статики. Чаще всего стержни рамы соединены между собой жестким образом, так, что в процессе деформации угол между стержнями не меняется. Мы будем рассматривать только плоские рамы, стержни которых расположены под углом 90°. Вертикальные стержни рамы принято называть стойками, горизонтальные – ригелями. В стержнях плоских рам возникают три внутренних усилия: продольная и поперечная силы и изгибающий момент.
Внутренние усилия в рамах определяются методом сечений, и порядок их нахождения тот же, что и для балок. Напомним, что согласно методу сечений:
•продольная сила N равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось стержня;
•поперечная сила Q равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось, перпендикулярную оси стержня;
•изгибающий момент M равен сумме моментов всех сил, действующих с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения.
Правила знаков для продольной и поперечной сил те же, что и раньше: растягивающая продольная сила положительна, поперечная сила положительна, если она обходит сечение по ходу часовой стрел-
ки. Правило знаков для изгибающего момента в рамах следующее:
момент считается положительным, если он изгибает стержень рамы

67
выпуклостью вовнутрь10. На эпюрах N и Q положительные значения принято откладывать снаружи, на эпюре М – внутри – со стороны растянутых волокон.
От действия трех внутренних усилий в стержнях рамы возникают напряжения: нормальные и касательные. Нормальные напряжения определяются как сумма напряжений от продольной силы ( N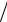 A) и от
A) и от
изгибающего момента по формуле (4.1). Касательные напряжения находят по формуле Журавского (4.2).
Перемещения точек оси рамы определяются, как правило, методом Максвелла – Мора по формуле (4.21). Заметим, что произвольная точка оси рамы в отличие от точки оси балки может перемещаться не только по вертикали, но и по горизонтали. Будем обозначать линейные перемещения точек оси рамы буквой δ, отмечая направление перемещения индексом сверху: δверти δгор. Углы поворота сечений рамы, как и балок, обозначаем буквой ϕ.
Примеры решения задач
4.2.1. Определение внутренних усилий в рамах (задачи № 21, 22)
Условие задачи
Рассмотрим раму, показанную на рис. 4.26, и определим в ней внутренние усилия, то есть построим эпюры N, Q и М.
Решение
Найдем три опорные реакции, используя три уравнения статики. Желательно составлять такие уравнения, чтобы в каждое из них входила бы только одна неизвестная реакция. В данном примере это такие уравнения (предполагаемые направления реакций показаны на рис. 4.27, а):
10 Для некоторых рам невозможно определить, где внешняя часть рамы, а где внутренняя. В этом случае знак изгибающего момента не определяется и эпюра изгибающих моментов строится со стороны растянутых волокон без знака.
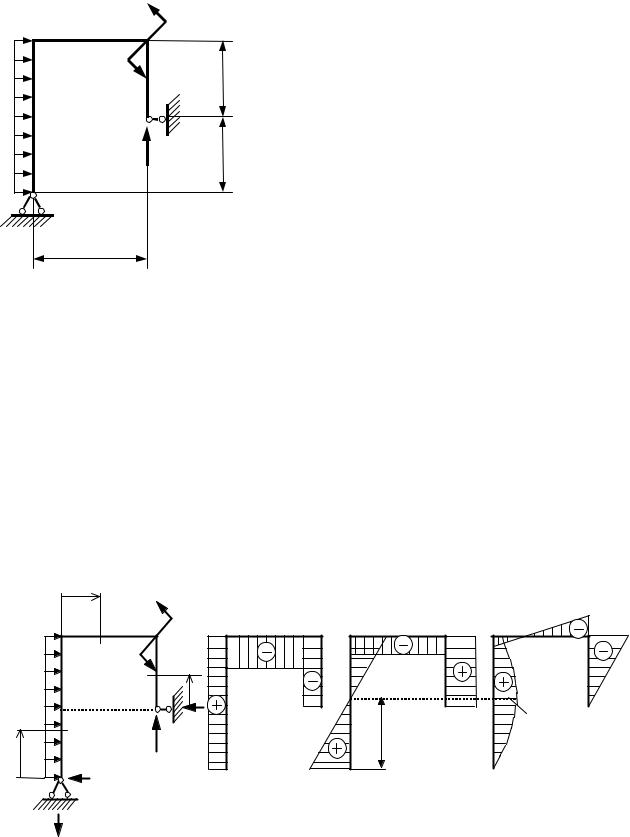
68
М=30 кН м |
|
q=20 кН/м |
2 м |
|
|
B |
|
F=20 кН |
2 м |
|
|
А |
|
3 м |
|
Рис. 4.26. Схема рамы |
|
с нагрузками |
|
∑mA = 0 ;
F 3 + M − q 4 2 + H B 2 = 0 ;
H B = 35 кН;
∑ проекций сил на вертикальную
ось равна 0; |
F − RA = 0 ; |
RA = 20 кН; |
|
∑mC = 0; |
F 3 + M − H A 2 = 0 ; |
H A = 45 кН. |
|
Для проверки используем уравнение "сумма проекций сил на горизонтальную ось равна нулю":
H A + H B − q 4 = 45 +35 −20 4 = 0 .
Находим внутренние усилия, используя метод сечений. Рама имеет три участка. Заметим, что если для балки границей между участками считалось сечение, где появлялся новый силовой фактор, то для рам границей между участками является также и узел, где соединяются соседние стержни рамы (стойка и ригель). Рассечем стержни рамы на трех участках и выберем начало отсчета х на каждом участке (удобно начало отсчета выбирать в начале участка – рис. 4.27, а). Запишем выражения для продольной, поперечной сил и изгибающего
а |
x2 |
М=30 кНм б |
в |
г |
40 |
|
|
D |
E |
|
35 |
20 |
|
|
|
70 |
||||
|
|
|
|
20 |
|
|
|
q=20 кН/м |
x3 |
35 |
|
|
|
|
C |
B |
|
20 |
35 |
Mmax=50,6 |
|
|
|
HB |
|||
x1 |
F=20 кН |
2,25 м |
|
|
||
|
A |
HA |
20 |
45 |
|
|
RA |
ЭпюраN |
Эпюра Q |
ЭпюраM |
|
|
|
Рис. 4.27. Определение внутренних усилий в раме:
а – схема рамы с нагрузками; б, в, г – эпюры внутренних усилий
69
момента на каждом участке, используя вышеприведенные определе-
ния этих усилий и правила знаков для них: |
|
|||||
участок 1: |
0 ≤ x1 ≤ 4 м; |
|
|
|||
N (x1 ) = RA = 20 кН; |
|
|
|
|||
Q(x1 ) = H A −q x1 = 45 −20x1 ; |
|
|
||||
|
|
qx2 |
= 45 x −10 x2 |
|
||
M (x ) = H |
A |
x − |
1 |
; |
||
|
||||||
1 |
1 |
2 |
1 |
1 |
|
|
|
|
|
|
|
|
|
участок 2: |
0 ≤ x2 ≤ 3м; |
|
|
|||
N (x2 ) = H A −q 4 = −35кН; |
|
|
||||
Q(x2 ) = −RA = −20кН;
M (x2 ) = H A 4 − q 4 2 − RA x2 = 45 4 − 20 8 − 20 x2 =
= 20 − 20 x2 ;
участок 3: 0 ≤ x3 ≤ 2 м;
N (x3 ) = −F = −20 кН; Q(x3 ) = H B = 35кН;
M (x3 ) = −H B x3 = −35 x3 .
Строим эпюры усилий, используя написанные выражения (рис. 4.27, б, в, г). Значение максимального момента определяем так же, как в балках.
Проверку правильности построения эпюр в рамах производим, проверяя равновесие узлов. Для этого вырезаем узлы (в рассматриваемой раме их два: D и E) и прикладываем к сечениям, примыкающим к узлам, все внутренние усилия согласно построенным эпюрам.
|
|
|
Узел D |
Узел Е |
|
|
|
|
|
|
Направление усилий должно со- |
|||||||
|
|
|
|
|
|
|
|
|
ответствовать их знакам. На |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|||||
20 |
20 |
|
|
|
|
|
рис. 4.28 показаны вырезанные |
|||||||||||
|
35 |
|
35 |
|
|
|
|
|
|
|
|
из рамы узлы D и E вместе с |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
35 |
|
|
|
40 |
20 |
|
|
|
|
|
|
35 |
|
действующими в сечениях, при- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мыкающих к узлам, внутренни- |
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|||
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ми усилиями. Видно, что узлы |
||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
находятся в равновесии. Из ус- |
|||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
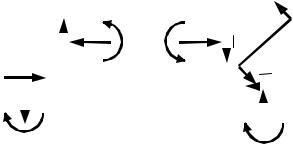
ловия равновесия узлов следует, что, если в узле не приложена внешняя пара сил (узел D), то
70
изгибающие моменты в сечениях, примыкающих к узлу, обязательно одинаковы. То есть, зная изгибающий момент в угловой точке для стойки, можно получить графически ординату М в угловой точке для ригеля, проведя циркулем дугу из вершины угла, как из центра. Если в узле действует сосредоточенная пара сил, то значения изгибающих моментов в примыкающих сечениях отличаются на величину этой пары.
4.2.2. Определение перемещений в рамах (задачи № 21, 22)
Условие задачи
Для рамы, показанной на рис. 4.26, найдем вертикальное перемещение точки В и угол поворота сечения А. Жесткость стержней рамы будем считать одинаковой ( EI = const ). Перемещения ищем методом Максвелла – Мора, интегрируя формулу Максвелла – Мора аналитически и графически (с помощью правила Верещагина).
Решение
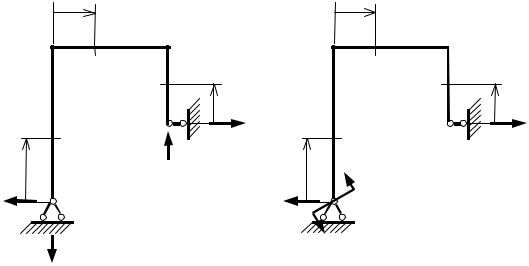
Будем искать первое обобщенное перемещение – вертикальное перемещение точки В. В соответствии с методом Максвелла – Мора для определения этого перемещения приложим в точке В единичную вертикальную сосредоточенную силу (рис. 4.29, а) и найдем изги-
х2 |
х2 |
a |
б |
|
В |
х3 |
|
В |
х3 |
|
3/2 |
|
|
||
х1 |
1 |
1/2х1 А |
1 |
1/2 |
|
А |
|
|
3/2
1
Рис. 4.29. Рама под действием единичной обобщенной силы: а – соответствующей δвертB ; б – соответствующей ϕA
