
Левченко 2 часть
.pdf
91 |
|
I xпC yC = Aпab , |
(4.36) |
где Aп = δ h = li – площадь прямоугольника ( δ =1, h = li ); a, b – координаты центра тяжести прямоугольника в системе координатных осей xc, yc; I xп0 , I пy0 – моменты инерции прямоугольника относитель-
но собственных центральных осей x0, y0, параллельных осям xc, yc. Если ось x0 (или y0) расположена вдоль рассматриваемого участка
трубопровода, то есть параллельна |
стороне прямоугольника li, то |
||
можно считать I xп0 = 0 (или I пy0 |
= 0). Если же ось x0 (или y0) перпен- |
||
дикулярна стороне li, то I xп0 = I |
пy0 = |
li3 |
. В формуле (4.36) учтено, что |
|
|||
|
12 |
|
|
центробежный момент инерции прямоугольника I xп0 y0 относительно
собственных осей x0, y0 равен нулю, так как эти оси являются главными осями инерции прямоугольника.
После определения величин лишних неизвестных по формулам (4.30) – (4.32) строим эпюры внутренних усилий в основной системе, как в обычной статически определимой раме. Эпюру изгибающих моментов можно проверить следующим образом. В упругом центре приложим найденные силы Х1 и Х2, нарисовав их в масштабе. Определим графически равнодействующую этих сил. Точки пересечения линии действия этой равнодействующей с осью рамы – это точки, в которых изгибающий момент должен равняться нулю (точки A, B, D
на рис. 4.46, б).
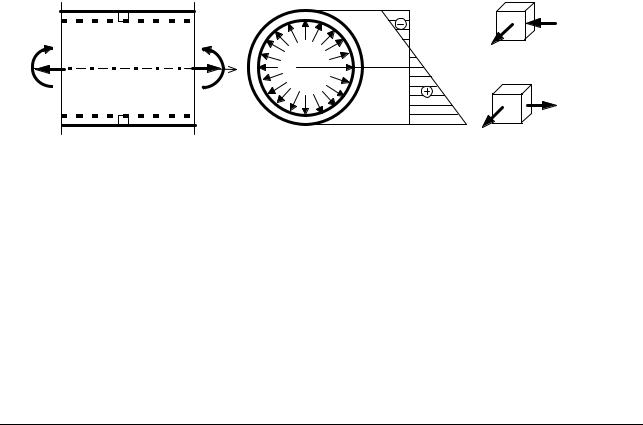
Построив эпюры внутренних усилий, проверим прочность конструкции, имея в виду, что поперечное сечение стержней рамы – труба и, кроме температурного воздействия, труба испытывает действие внутреннего давления. Максимальные нормальные напряжения σх, действующие на площадках, перпендикулярных оси трубы, находим, складывая напряжения от продольной силы и максимального изгибающего момента в опасном сечении рамы14:
14 При определении напряжений от изгиба на криволинейных участках трубы в местах сопряжения вертикальных и горизонтальных стержней рамы не
|
|
92 |
|
|
|
|
|||
σx = |
N |
± |
|
|
M max |
|
|
. |
(4.37) |
|
|
|
|||||||
|
|
||||||||
A |
|
|
|
|
|
||||
|
|
|
|
W |
|
||||
Для проверки прочности трубы из пластичного материала по формуле (4.37) находим максимальное по модулю напряжение. Если труба выполнена из хрупкого материала, при проверке прочности важен знак напряжений. Кольцевое напряжение σθ , возникающее от внутреннего давления q, определяем по формуле
σθ = |
qR |
, |
(4.38) |
|
δ |
||||
|
|
|
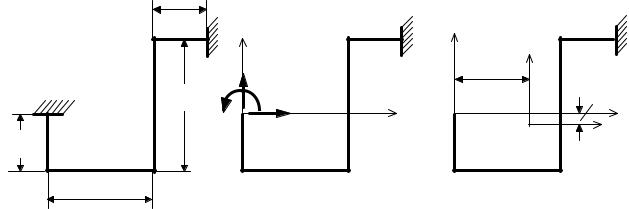
где R и δ – соответственно внешний радиус и толщина трубы. Напряжение σθ всегда растягивающее. На рис 4.47, а показана эпюра распределения напряжений σх в опасном сечении при положительной продольной силе. Рис. 4.47, б изображает напряженное состояние опасных точек 1, 1′. Так как касательные напряжения на площадках элементов, показанных на рис. 4.47, б, отсутствуют, то эти площадки
|
а |
|
б |
|
|
|
1 |
|
σcmax |
|
σcmax |
Mmax |
|
|
1 |
||
Mmax |
q |
|
|
||
|
x |
|
σθ |
|
|
N |
N |
|
|
1′ |
σрmax |
|
|
|
|||
|
1′ |
|
σрmax |
σθ |
|
Рис. 4.47. К определению напряжений в трубе:
а– распределение напряжений σх в опасном сечении;
б– напряженное состояние опасных точек
являются главными. Проверку прочности в опасных точках осуществляем по теории прочности, соответствующей материалу трубы.
учитываем эффект Кармана, связанный со сплющиванием поперечного сечения трубы и приводящий к уменьшению изгибных напряжений.
93
Пример расчета трубопровода (задача № 26)
Условие задачи
Трубопровод, показанный на рис. 4.48, а, нагревается на ∆Т градусов и подвержен действию внутреннего давления q. Труба имеет внешний радиус поперечного сечения R и толщину δ. Известен материал трубы. Требуется найти напряженное состояние и обеспечить выполнение условия прочности трубопровода.
Решение
а |
y б |
|
y |
в |
yc |
4 |
|
|
X2 |
|
|
xc |
|
|
|
|
|
|
3 |
|
|
||
l3=2м |
X3 |
х |
O |
|
yc |
х |
|
|
O |
|
|
|
|||
|
|
|
C |
|
хc |
||
l1=1м |
X1 |
|
1 |
|
|
||
|
|
|
|
|
|
l2=2м |
2 |
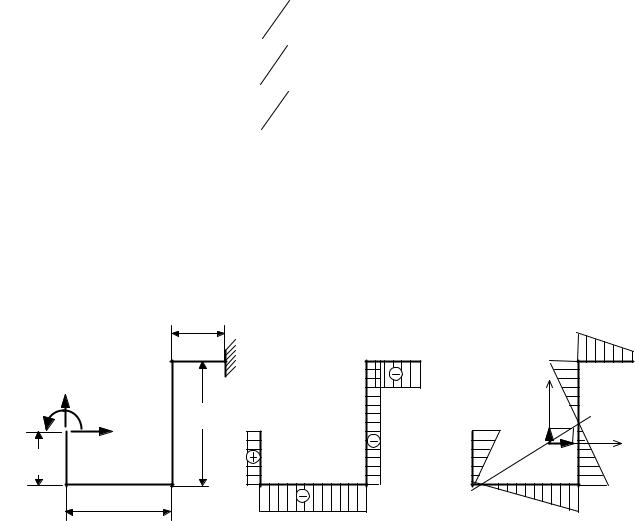
Рис. 4.48. К примеру расчета трубопровода: а – заданная систкма;
б– основная система;
в– положение упругого центра
Выберем основную систему, отбросив левое закрепление и приложив реактивные силы (лишние неизвестные) Х1, Х2 и Х3 (рис. 4.48, б). Для определения значений лишних неизвестных по формулам (4.30) – (4.32) найдем сначала положение упругого центра и геометрические характеристики I xC , I yC и I xC yC .
Координаты упругого центра в системе координат xОy сосчитаем по формулам (4.33), где
A = l1 + l2 + l3 + l4 = 6 м.
Статический момент относительно оси х равен сумме статических моментов четырех прямоугольников единичной толщины:
94
Sx = Sx(1) + Sx(2) + Sx(3) + Sx(4) .
Статический момент третьего участка трубопровода (третьего прямоугольника) Sx(3) = 0, так как центр тяжести этого прямоугольни-
ка лежит на оси х, а статические моменты остальных прямоугольников найдем следующим образом:
|
S(1) |
= l (−l |
/ 2) =1 (−0,5) = −0,5 м2, |
|||||
где l1 1 = l1 |
x |
1 |
|
1 |
|
|
|
|
– площадь первого прямоугольника, а (– l1 / 2 ) – коорди- |
||||||||
ната центра тяжести. Аналогично |
||||||||
|
S |
(2) = l |
2 |
(−l ) = 2 (−1) = −2 м2, |
||||
|
|
x |
|
1 |
|
|
||
Таким образом, |
Sx(4) |
= l4 l3 / 2 =1 1 =1 м2. |
||||||
|
|
|
|
−1,5 |
|
|
||
|
|
|
yc |
= |
= −0,250 м. |
|||
|
|
6 |
||||||
|
|
|
|
|
|
|
|
|
Вторая координата упругого центра |
||||||||
|
xc = |
0 +2 1+2 2 +1 2,5 |
=1,42 м. |
|||||
|
|
|||||||
|
|
|
|
|
|
6 |
|
|
Отложим эти координаты на рисунке и покажем точку С – упру- |
||||||||
гий центр. |
Проведем |
через |
точку С центральные оси xc, yc |
|||||
(рис. 4.48, в). Найдем моменты инерции фигуры относительно этих осей. Момент инерции относительно оси хс равен сумме моментов инерции четырех прямоугольников:
(1) |
(2) |
(3) |
(4) |
I xC = I xC |
+ I xC |
+ I xC |
+ I xC . |
Сосчитаем момент инерции первого прямоугольника относительно оси хс по формуле (4.34). Для рассматриваемого прямоугольника собственная ось х0 перпендикулярна стороне l1, поэтому первый член в (4.34) (момент инерции первого прямоугольника собственной оси х0 ) не равен нулю. Таким образом, момент инерции относительно оси хс
I (1) = |
l13 |
+ A(1)a2 |
= |
13 |
+1 0,252 = 0,146 м3. |
|
|
||||
xC |
12 |
(1) |
12 |
|
|
|
|
|
|||
Для второго прямоугольника момент инерции относительно оси хс
95
(2) |
= A |
(2) |
2 |
= 2 0,75 |
2 |
=1,125 |
3 |
. |
I xC |
|
a(2) |
|
м |
Поскольку ось х0 параллельна стороне прямоугольника l2, то
первое слагаемое в формуле (4.34) отсутствует ( I |
(2) = 0 ). Аналогично |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
находим моменты инерции остальных прямоугольников: |
|||||||||||||||||||||||||
|
|
|
|
|
I |
(3) |
= |
23 |
+ 2 0,252 = 0,792 м3; |
|
|||||||||||||||
|
|
|
|
|
xC |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
I (4) |
=1 1,252 |
=1,562 м3. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
xC |
|
|
|
|
|
|
|
|
относительно оси хс равен |
|||||||
И полный |
момент |
инерции |
|||||||||||||||||||||||
I xC = 3,625м3. Так же вычислим момент инерции относительно оси yc |
|||||||||||||||||||||||||
каждого прямоугольника: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(1) |
|
|
|
(1) |
|
2 |
|
=1 |
1,42 |
2 |
|
3 |
; |
|||||||||||
|
I yC |
= |
A |
b(1) |
|
|
= 2,016 м |
||||||||||||||||||
I (2) = |
l2 |
3 |
|
|
+ A(2) b2 |
|
|
= |
23 |
|
+ 2 0,422 |
=1,020 м3; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
yC |
12 |
|
|
|
|
|
|
(2) |
|
12 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(3) |
|
|
|
(3) |
2 |
= 2 |
|
|
|
2 |
|
3 |
; |
|||||||||||
|
I yC |
= |
A |
|
b(3) |
0,58 |
= 0,673 м |
||||||||||||||||||
I (4) = |
l4 |
3 |
|
+ A(4) b2 |
|
|
= |
13 |
+1 1,082 |
=1,249 м3. |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
yC |
12 |
|
|
|
|
|
(4) |
12 |
|
|
|
|
|
||||||||||||
Полный момент инерции относительно оси yc равен сумме мо- |
|||||||||||||||||||||||||
ментов инерции всех прямоугольников I yC |
= 4,958 м3. |
|
|||||||||||||||||||||||
Найдем центробежный момент инерции. Момент инерции каждого прямоугольника определим по формуле (4.36). Обратим внимание на то, что, если при вычислении осевых моментов инерции знаки координат а и b можно опускать, так как они входят в формулы (4.34), (4.35) в квадрате, то при вычислении центробежного момента инерции эти знаки следует обязательно учитывать. Тогда
I (1) |
=1 (−0,25) (−1,42) = 0,355 м3; |
|
xC yC |
|
|
I (2) |
= 2 (−0,75) (−0,42) = 0,630 м3; |
|
xC yC |
|
|
|
I (3) |
= 2 0,25 0,58 = 0,29 м3; |
|
xC yC |
|
|
I (4) |
=1 1,25 1,08 =1,35 м3. |
|
xC yC |
|
96
Полный центробежный момент инерции IxC yC = 2,625 м3. Длины трубопровода вдоль осей х и y: Lx = 3м, Ly = −1 + 2 =1м.
Подставляя найденные геометрические характеристики в формулы (4.30)–(4.32), сосчитаем значения лишних неизвестных:
X1 α∆TEI =1,58м–2;
X 2 α∆TEI =1,04 м–2;
X 3 α∆TEI =1,87 м–1.
Нарисуем основную систему и приложим в точке О найденные опорные реакции. Так как все лишние неизвестные оказались положительными, то сохраняем выбранное ранее направление всех неизвестных (рис. 4.49, а). Построим эпюры продольных сил и изгибающих моментов в долях от α∆TEI (рис. 4.49, б, в). На рис. 4.49, в показана равнодействующая сил Х1 и Х2, приложенных в упругом центре.
|
а |
|
l4=1м |
б |
|
|
|
||
|
X2=1,04 |
|
|
|
|
|
X3=1,87 |
l3=2м |
1,04 |
l1=1м |
О |
X1=1,58 |
|
|
|
|
|
|
|
|
|
l2=2м |
1,58 |
|
|
в |
1,37 |
0,33 |
|
|
||
|
1,58 |
yc |
|
|
|
|
|
|
1,87 |
|
|
|
|
C |
хc |
1,04 |
|
|
|
0,29 |
|
|
|
|
|
|
1,79 |
Рис. 4.49. Определение внутренних усилий в трубопроводе:
а– основная система с найденными реакциями в долях от α∆TЕI;
б– эпюра продольных сил N в долях от α∆TЕI;
в– эпюра изгибающих моментов М в долях от α∆TЕI
Видно, что на линии действия этой равнодействующей изгибающий момент равен нулю.
Теперь можно решать вопрос о проверке прочности трубы. По эпюрам N и М находим опасное сечение. У нас это сечение в точке О

97
(рис. 4.49, а). 15 В этом сечении действуют одновременно максималь-
ный |
изгибающий |
момент и растягивающая продольная сила: |
||
|
M max |
|
=1,87α∆TEI , |
N =1,04α∆TEI . Напряжения в опасных точках |
|
|
|||
вычисляем по формулам (4.37) и (4.38). Для удобства расчетов приведем формулу (4.37) к другому виду. Максимальное напряжение от изгиба
σmaxM |
|
= |
|
M max |
|
|
= |
1,87α∆TEI |
=1,87α∆TER, |
|
|
|
|
||||||||
|
||||||||||
|
|
|
||||||||
|
W |
|
W |
|||||||
|
|
|
|
|
|
|
||||
так как момент сопротивления W = I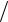 R . Нормальное напряжение, вызванное продольной силой, найдем так:
R . Нормальное напряжение, вызванное продольной силой, найдем так:
|
|
σ |
N |
= |
N |
= |
1,04α∆TEI |
=1,04α∆TE |
|
R2 |
[1 +( |
r |
) |
2 |
], |
|
|
|
|
|
|||||||||||||||
|
|
|
|
A |
|
|
A |
|
|
|
|
|
4 |
R |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где учтено, что для трубы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
I = |
πR4 |
− |
πr |
4 |
= |
πR |
4 |
[1−( |
r |
) |
4 |
], |
A = πR |
2 |
−πr |
2 |
= πR |
2 |
[1 |
−( |
r |
) |
2 |
], |
|||||||||||
4 |
|
4 |
|
|
4 |
|
|
R |
|
|
|
|
|
R |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r – внутренний радиус трубы. Суммарные напряжения на площадках, перпендикулярных оси х, находим согласно (4.37), складывая σN и
σmaxM .
Отметим особенность решаемой задачи об определении температурных напряжений в статически неопределимой раме: чем больше размер поперечного сечения (больше радиус трубы), тем больше возникающие в конструкции температурные напряжения. Это связано с тем, что с увеличением радиуса увеличивается жесткость рамы и уменьшается свобода деформаций, что и приводит к увеличению напряжений.
Вычисляя напряжения в опасных точках, обратите внимание на единицы измерения величин, входящих в формулы для напряжений.
В формуле для определения σmaxM число 1,87 имеет размерность м–1, в
формуле для σN число 1,04 измеряется в м–2. Таким образом, подставляя R в метрах, получим величину напряжения в тех же единицах измерения, что и модуль упругости Е. При проверке прочности в
15 В рассматриваемом примере опасным сечением может быть также сечение, в котором действуют усилия M =1,79α∆TEI и N = −1,58α∆TEI .
98
опасных точках трубы используйте знания, полученные при изучении разд. 2 "Исследование плоского напряженного состояния. Проверка прочности для сложного напряженного состояния" [5]. Если условие прочности выполняться не будет, следует уменьшить радиус трубы и добиться удовлетворения условия прочности.

99
4.5. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В КРИВОЛИНЕЙНОМ СТЕРЖНЕ
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление мате-
риалов. М.: Высш. шк., 1995. Гл. 2 (§ 2.6), гл. 6 (§ 6.10).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 11 (§ 46, 47).
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 10 (§ 10.1–10.3).
Беляев Н. М. Сопротивление материалов. М., 1976.§ 132–139.
Основные определения
В плоском криволинейном стержне так же, как в плоской раме, состоящей из прямолинейных стержней, возникает три внутренних усилия: N, Q и М. Процесс определения внутренних усилий в криволинейном стержне тот же, что и в раме. Особенность состоит в новом правиле знаков для изгибающего момента: изгибающий момент считается положительным, если он увеличивает кривизну стержня16. Правила знаков для продольной и поперечной сил те же, что и при их определении в плоских рамах.
При чистом изгибе в криволинейных стержнях возникают нормальные напряжения, которые вычисляются по формуле
σ = |
M |
|
z0 + z |
, |
(4.39) |
|
Az0 |
R + z |
|||||
|
|
z0 |
|
|||
где R – радиус кривизны оси стержня; |
– величина смещения ней- |
|||||
тральной оси от главной центральной оси сечения в сторону центра кривизны (точка С на рис. 4.50); z – координата той точки, в которой мы ищем напряжения в главной центральной системе координат. Для того, чтобы формула (4.39) при определении напряжений правильно
16 Если рассматриваемый стержень имеет и прямолинейный, и криволинейный участки, то для того, чтобы не было противоречия из-за разного правила знаков для изгибающего момента в прямолинейной и криволинейной частях стержня, принято строить эпюру изгибающего момента со стороны растянутых волокон без определения знака.

100
давала знак напряжений, ось z следует направлять в сторону от центра кривизны. Формула (4.39) показывает, что нормальные напряжения в поперечном сечении криволинейного стержня распределяются не по линейному закону, как в прямолинейном стержне, а по гиперболическому. Эпюра нормальных напряжений в криволинейном стержне при чистом изгибе показана на рис. 4.50.
Для определения величины z0 существуют разные пути. Будем
M |
z |
|
|
|
y |
|
z0 |
R |
Эпюра σ |
 С
С
Рис. 4.50. Распределение напряжений в сечении кривого бруса при чистом изгибе
делить криволинейные стержни в зависимости от отношения R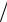 c
c
(где с – расстояние от центра тяжести сечения до крайнего внутреннего волокна) на стержни
большой |
( R c < 4), |
средней |
(4 ≤ R c ≤10) |
и малой |
кривизны |
( R c >10). Для стержней большой кривизны при определении z0 ре-
c >10). Для стержней большой кривизны при определении z0 ре-
комендуем использовать точные формулы для простых форм сечений (прямоугольник, круг), полученные в [2, § 46]. Если поперечное сечение имеет более сложную формулу, то при определении величины z0 для стержней большой и
средней кривизны можно использовать либо приближенные формулы [2, § 46], либо таблицы, приведенные в [7, § 139]. Для стержней малой и средней кривизны допустимо использовать приближенную формулу
z0 = |
I y |
|
. |
(4.40) |
|
RA |
|||||
|
|
|
|||
Если в сечении, кроме изгибающего момента, действует продольная сила, то в формулу (4.39) добавляется слагаемое N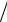 A. Каса-
A. Каса-
тельные напряжения от поперечной силы в практических расчетах для криволинейных стержней обычно не учитывают.
Для определения перемещений точек оси криволинейных стержней большой кривизны используется метод Максвелла – Мора, согласно которому обобщенное перемещение δi находится по форму-
ле [2]
