
Левченко 2 часть
.pdf
31
нию Wy там соответствует Wx ). Для балки, изображенной на
рис. 4.10, выполненной из стали С-235 с допускаемым напряжением
160 МПа,
Wyнеобх ≥ 860016 = 537,5 см3,
и в соответствии с ГОСТ 9239–89 подбираем двутавр № 33, у которого Wy = 597см3.
После того, как найден номер двутавра, необходимо убедиться, что выполняются условия прочности в остальных опасных точках. Точка 2, в которой нормальные напряжения равны нулю, а касательные – максимальны, находится в напряженном состоянии "чистый сдвиг" и условие прочности в ней записывается по теории прочности, справедливой для пластичных материалов (4.9) или (4.10). Максимальные касательные напряжения находим по формуле Журавского (4.2). Рассмотрим подробно как находить статический момент отсе-
ченной части S yо(z) , входящий в формулу Журавского. Статический |
|||||||
момент отсеченной части зависит от того, где находится точка, в ко- |
|||||||
торой определяется касательное напряжение. Чтобы найти отсечен- |
|||||||
ную часть, надо мысленно разрезать поперечное сечение через точку, |
|||||||
|
|
|
|
|
в которой ищем τ, |
||
|
а |
б |
|
|
перпендикулярно |
||
|
|
|
направлению |
каса- |
|||
|
s |
3 |
τ |
|
тельного |
напряже- |
|
|
|
ния. Любая из "от- |
|||||
h |
τ |
h |
s |
|
резанных" |
частей |
|
|
2 |
y |
|
y |
может |
считаться |
|
|
|
|
|
|
отсеченной. |
Для |
|
|
t |
t |
|
|
точки 2 отсеченная |
||
|
z |
|
z |
|
часть сечения пока- |
||
|
b |
|
b |
|
зана на рис. 4.11, а |
||
|
Рис. 4.11. Отсеченные части сечения: |
|
(заштрихованная |
||||
|
|
часть) – это поло- |
|||||
|
|
а – для точки 2; |
|
|
вина сечения. Для |
||
|
|
б – для точки 3 |
|
|
простых |
|
фигур |
|
|
|
|
|
|
||

32
(прямоугольник, круг), положение центра тяжести которых известно, статический момент находится по формуле
S y = A zцт,
где А – площадь фигуры; zцт– координата центра тяжести (при вы-
числении статического момента отсеченной части знак координаты не учитывается, в этом случае zцт – это расстояние от центра тяжести
отсеченной части до оси y). Для вычисления статического момента отсеченной части, показанной на рис. 4.11, а , разобьем ее на два прямоугольника: полку и половину стенки. Для каждого прямоугольника находим площадь и расстояние от центра тяжести до оси y. Тогда
S оy = bt(h2 − 2t ) + (h2 − t)s 12 (h2 − t) .
В этой формуле первое слагаемое – статический момент полки, а второе – статический момент половины стенки. Заметим, что для стандартных двутавров статический момент половины сечения задан
в сортаменте (обозначен Sx ) и для найденного двутавра |
№ 33 |
S yо = 339см3. В формуле Журавского (4.2) для точки 2 b(z) = s |
– тол- |
щина стенки двутавра, I y – осевой момент инерции находим по таблице сортамента прокатных двутавров (обозначенI x ) . Подставляя
данные для двутавра № 33, получим
τmax = 41,9 339 = 2,06 кН/см2. 9840 0,7
Сравнивая максимальное касательное напряжение согласно третьей теории прочности с [σ]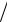 2 = 8 кН/см2 , убеждаемся, что усло-
2 = 8 кН/см2 , убеждаемся, что усло-
вие прочности в точке 2 выполняется.
Проверим прочность в точках 3, 3′, которые находятся в "балочном" напряженном состоянии (см. рис. 4.4). Найдем напряжения, действующие в точке 3. Нормальное напряжение ищем по формуле (4.1). Координата точки 3 z = −(h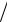 2 −t) и
2 −t) и
σ = −6610 (−16,5 +1,12) =10,3 кН/см2. 9840

33
Положительный знак полученного напряжения показывает, что в точке 3, расположенной выше нейтральной оси, действует растягивающее напряжение. Для определения касательного напряжения по формуле Журавского получим сначала статический момент отсеченной части. Отсеченной частью сечения для точки 3 будет полка (см.
рис. 4.11, б) и
S оy =14 1,12 (16,5 −1,12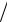 2) = 250 см3.
2) = 250 см3.
Так как точка 3 находится в стенке двутавра, то b(z) = s = 0,7 см.
Тогда касательное напряжение в точке 3
τ = 38,1 250 =1,38 кН/см2. 9840 0,7
Подставляя найденные значения σ и τ в условие прочности по третьей теории (4.9), убеждаемся в том, что оно удовлетворяется:
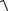 10,32 +4 1,382 =10,7 < 16 кН/см2.
10,32 +4 1,382 =10,7 < 16 кН/см2.
На этом процесс подбора двутавра заканчивается.
При решении задачи № 17 требуется еще исследовать напряженное состояние произвольной точки двутавра. Эта часть задачи не имеет отношения к проверке прочности двутавра, носит академический характер и необходима для лучшего освоения теории изгиба. После того, как Вы выбрали произвольную точку, расположенную в сечении, где и Q, и М не равны нулю, найдите нормальное и касательное напряжения в этой точке по формулам (4.1), (4.2), используя те навыки, которые Вы приобрели при определении напряжений в опасных точках. Выделите вокруг исследуемой точки элементарный параллелепипед (элемент) и покажите на рисунке действующие на гранях элемента напряжения с учетом их знаков. Дальше определите главные напряжения и положение главных площадок, применяя знания, полученные при изучении разд. 2 "Исследование плоского напряженного состояния" в [5]. Поверните на рисунке элемент по главным направлениям и покажите на его гранях главные напряжения.
Пример 3
Условие задачи
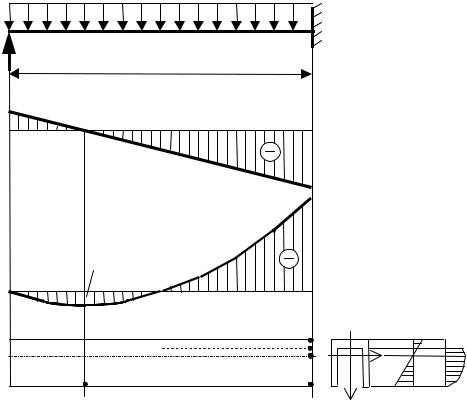
34
На балку моносимметричного сечения, выполненную из чугуна, действует нагрузка, показанная на рис. 4.12, а. Поперечное сечение балки изображает рис. 4.13. Надо найти грузоподъемность балки, т. е. значение допускаемой нагрузки, при которой обеспечены прочность и жесткость балки. Допускаемое значение максимального прогиба балки задано.
Решение
Найдем геометрические характеристики заданного поперечного сечения: осевые моменты инерции относительно главных центральных осей. Сечение имеет только одну ось симметрии, эта ось являет-
a |
|
q |
|
|
|
|
|
|
|
F=ql/4 |
|
l |
|
|
б |
|
|
|
|
ql/4 |
|
|
Эпюра Q |
|
|
|
|
||
|
|
|
3ql/4 |
|
|
|
|
ql2/4 |
|
|
|
ql2/32 |
Эпюра M |
|
|
|
|
||
в |
b |
1 |
a |
|
|
|
3 |
|
|
|
4 |
2 |
|
y |
|
1′ a |
|
||
|
b |
z Эп. σ Эп. τ |
||
|
|
|
|
|
Рис. 4.12. К решению примера 3 о проверке прочности балки:
а– схема балки с нагрузками;
б– эпюры поперечной силы и изгибающего момента;
в– опасные сечения и опасные точки
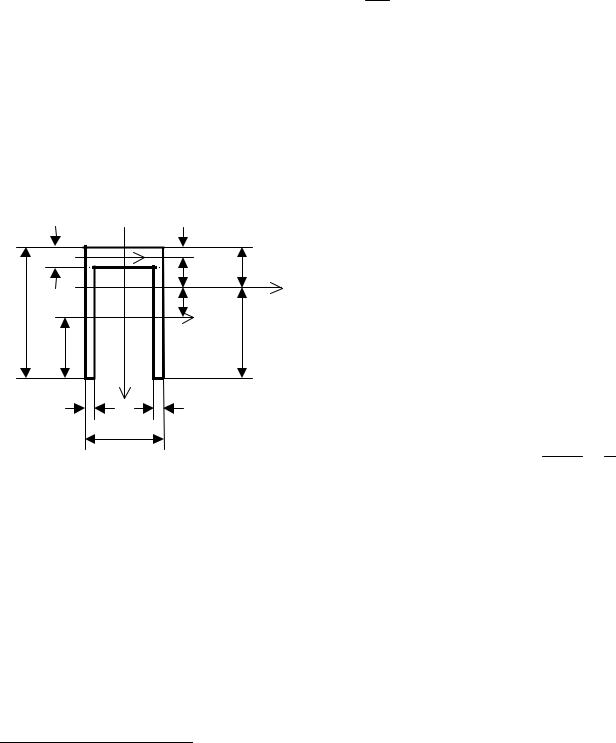
35
ся одной из главных осей инерции. Обозначим ее z. Вторая главная ось y проходит через центр тяжести сечения. Определим положение центра тяжести сечения по формуле
zцт = SAa .
Статический момент Sa определяем относительно произ-
вольной оси а–а, перпендикулярной оси z (оси симметрии), как сумму статических моментов фигур, составляющих заданное поперечное сечение. В данном случае сечение разбиваем на три прямоугольника и площадь сечения состоит из площадей трех фигур: двух стенок Ас и полки Ап: A = 2 Ac + Aп. Ось а–а рационально расположить так, чтобы
|
|
y0 |
t/2 |
|
t |
a |
|
a |
p |
|
|
|
zц т=h2 |
z max |
h |
|
|
h1 |
y |
|
|
y0 |
zсmax |
|
h-t |
|
|
||
|
|
|
|
|
2 |
|
z |
|
|
|
δ |
δ |
|
|
|
|
b |
|
|
Рис. 4.13. Поперечное сечение балки
ки5.
статический момент одной из фигур равнялся нулю. Это произойдет, если ось а–а провести через центр тяжести какой-то фигуры, например, через центр тяжести полки (см. рис. 4.13). Тогда статический момент полки равен нулю и полный статический момент Sa равен удвоенному статическому моменту стенки:
Sa = 2(h − t)δ (h 2− t + 2t ).
Здесь первый множитель – удвоенная площадь стенки, второй – координата центра тяжести стен-
Найдя положение центра тяжести сечения, проведем через него вторую главную ось y (см. рис. 4.13). Рекомендуем рисовать сечение в масштабе, тогда по масштабу можно проконтролировать правильность определения центра тяжести сечения. В данном случае очевидно, что центр тяжести должен быть смещен к полке.
5 При вычислении статического момента не забывайте учитывать знаки координат центра тяжести.
36
Теперь определим осевой момент инерции относительно оси y. Находим его как сумму моментов инерции трех фигур: двух стенок
( I c ) и полки ( I п). Для определения момента инерции каждой фигуры используем формулу
I y = I y0 + A a2 .
Здесь I y0 – момент инерции фигуры относительно оси y0, проходя-
щей через центр тяжести фигуры и параллельной оси y, а – расстояние между осями y и y0. Таким образом,
I y = 2(I сy0 + Aсh12 ) + I пy0 + Aпh22 .
Расстояния h1 и h2 показаны на рис. 4.13. Моменты инерции полки и стенки относительно собственных осей y0 находим по формуле, справедливой для прямоугольника,
I y0 = |
bh3 |
, |
|
12 |
|||
|
|
где b – ширина прямоугольника (параллельна оси y0); h – его высота. Например, для полки
I пy0 |
= |
bt3 |
. |
|
|||
|
12 |
|
|
Примечание. Рекомендуем для тренировки аналогично найти момент инерции поперечного сечения относительно оси z, несмотря на то, что в проверке прочности этой балки он не участвует.
Строим эпюры поперечной силы и изгибающего момента, выражая ординаты через неизвестный параметр нагрузки (в данной задаче через q – см. рис. 4.12, б).
Прежде чем находить положение опасных сечений и опасных точек по эпюрам Q и М, выясним как рационально расположить поперечное сечение балки: полкой вверх или полкой вниз. Поскольку чугун – хрупкий материал и прочность при растяжении у него меньше прочности при сжатии, оптимальным положением сечения является такое положение, при котором максимальные растягивающие напряжения будут меньше максимальных по модулю сжимающих напряжений. В рассматриваемом примере максимальный изгибающий момент отрицателен, то есть балка в сечении, где действует M max ,
37
изгибается выпуклостью вверх и растягивающие напряжения будут в верхних волокнах. Поэтому располагаем поперечное сечение так, чтобы центр тяжести сечения был ближе к верхним волокнам, т. е. полкой вверх.
Найдем положение опасных сечений и опасных точек так же, как в двутавровой балке (см. рис. 4.12, в). Поскольку максимальная поперечная сила и наибольший изгибающий момент действуют в данном примере в одном сечении, то опасные точки 1, 1′, 2 и 3 расположены в одном сечении а–а. Особенностью расчета балок из хрупкого материала является то обстоятельство, что точки 1 и 1′ не являются равноопасными. Так как хрупкий материал имеет разную прочность при растяжении и сжатии, то проверять прочность надо как в точке 1, в которой действуют максимальные растягивающие напряжения, так и в точке 1′ с наибольшими сжимающими напряжениями. Если эпюра изгибающих моментов меняет свой знак, как в рассматриваемом примере, то появляется еще одна опасная точка – точка 4 (см. рис. 4.12, в). В этой точке действуют растягивающие напряжения, и поскольку она расположена дальше от нейтральной оси, чем точка 1, величина растягивающего напряжения в точке 4 может оказаться больше, чем в точке 1 несмотря на то, что изгибающий момент в сечении b–b меньше, чем в сечении а–а.
Определим допускаемую нагрузку из условия прочности в точке 1, где действуют максимальные растягивающие напряжения:
|
|
|
|
|
|
р |
|
M max |
|
|
≤[σ]р, |
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
σmax = |
|
|
|
|
|
|
|
||
откуда |
|
|
|
Wр |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
M max |
|
≤Wр[σ]р. |
|
|||||||||
|
|
|
I y |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
Здесь Wр = |
|
|
|
|
– момент сопротивления растяжению; z maxр |
– рас- |
|||||||||
|
|
zmaxр |
|
|
|||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стояние до наиболее растянутого волокна показано на рис. 4.13. Для
рассматриваемого примера ql2 / 4 ≤W [σ] |
р |
и q ≤ 4 W [σ] |
р |
/ l2 . |
р |
р |
|

38
Проверим прочность в остальных опасных точках, используя найденное значение допускаемой нагрузки. В точке 1′ с наибольшими сжимающими напряжениями
|
|
|
|
|
|
σc |
|
= |
|
M max |
|
|
≤ [σ] , |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
max |
|
|
|
|
|
|
c |
|
|
|
I y |
|
|
|
|
|
|
Wc |
|||
|
|
|
|
|
|
|
|
||||||
где W |
= |
|
|
– момент сопротивления сжатию. (Расстояние zc |
|||||||||
|
zmaxс |
|
|||||||||||
с |
|
|
|
|
|
|
|
|
|
|
|
max |
|
показано на рис. 4.13.)
Для рассматриваемого примера опасной является и точка 4. Условие прочности в этой точке:
σ |
(4) |
= |
M b−b z(4) |
= |
M b−b |
≤[σ]р. |
|
I y |
Wc |
||||
|
|
|
|
|
Чтобы проверить прочность в точке 2 с максимальными касательными напряжениями, находящейся в напряженном состоянии "чистый сдвиг", необходимо применить теорию прочности, справедливую для хрупкого материала. Например, из теории Мора (4.8) для чистого сдвига получим следующее условие прочности:
τmax ≤ 1[σ+]kр ,
где максимальное касательное напряжение τmax определяем по формуле Журавского (4.2), в которой статический момент S оy находим
для отсеченной части, расположенной по одну (любую) сторону от нейтральной оси.
Наконец, условие прочности в точке 3, где действуют и нормальные (растягивающие), и касательные напряжения, записываем по теории прочности для "балочного" напряженного состояния, справедливой для хрупкого материала, например по теории Мора (4.8). Нормальные и касательные напряжения в этой точке определяем по фор-
мулам (4.1) и (4.2).
Если в какой-то точке условие прочности не будет выполняться, необходимо найти новое значение допускаемой нагрузки из условия прочности в этой точке.

39
В рассматриваемой задаче, кроме условия прочности, должно выполняться и условие жесткости, т. е. максимальный прогиб не должен превосходить значения допускаемого прогиба. Вопрос о нахождении прогибов решается в разделе "Определение перемещений и проверка жесткости балок".
4.1.3. Определение перемещений и проверка жесткости балок (задачи № 19, 20)
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление мате-
риалов. М.: Высш. шк., 1995. Гл. 8 (§ 8.1–8.5, 8.9).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 5 (§ 25), гл. 8.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 7 (§ 7.13–7.14), гл. 11 (§ 11.4, 11.5).
Основные определения
Под действием нагрузки происходит деформация балки: ось балки искривляется, точки оси балки перемещаются по вертикали6, сечения балки, оставаясь после деформации перпендикулярными изогнутой оси, поворачиваются. Вертикальное перемещение произвольной точки оси балки, то есть перемещение вдоль оси z , будем называть прогибом и обозначать w(х). Угол поворота произвольного сечения обозначим ϕ(х). Очевидно, что угол поворота произвольного сечения равен углу поворота оси балки в сечении x . Прогибы и углы поворота трех балок показаны на рис. 4.14. Известно, что функции w(х) и ϕ(х) связаны между собой такой зависимостью:
|
dw |
′ |
|
|
ϕ(x) = dx |
(4.14) |
|||
= w (x) . |
||||
6 Перемещения точек оси по горизонтали гораздо меньше вертикальных перемещений и ими будем пренебрегать.
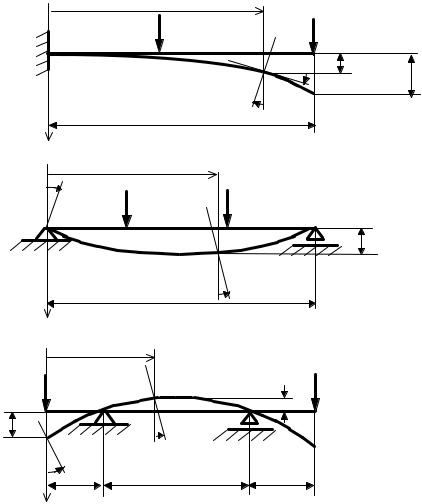
40
При проектировании конструкций часто ограничивают не только напряжения (требуется удовлетворить условию прочности), но и деформации (требуется обеспечить выполнение условия жесткости). Для балок условием жесткости является условие, ограничивающее максимальный прогиб, т. е.
wmax ≤[w], |
(4.15) |
где [w] – допускаемый прогиб, который задается в долях от длины
пролета балки l и в зависимости от типа проектируемой конструкции может находиться в пределах от l 200 до l
200 до l 1000 .
1000 .
Рассмотрим два наиболее часто используемых способа определения перемещений балок (прогибов и углов поворота): способ, ос-
a |
|
|
|
|
|
|
|
х |
|
|
|
|
A |
|
|
w(x) |
|
|
|
|
|
wmax |
|
|
|
|
ϕ(x) |
ϕ(x) |
|
|
|
|
|
||
z |
|
l |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
б |
|
x |
|
|
|
|
|
|
|
|
|
A |
ϕ0 |
|
|
B |
|
|
|
|
|
||
|
|
|
|
w(x) |
|
|
|
l |
ϕ(x) |
|
|
|
|
|
|
|
|
z |
|
x |
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
w(x) |
|
|
|
|
|
|
|
|
w0 |
|
ϕ(x) |
B |
|
|
|
|
a |
|
|
|
ϕ0 |
a |
l |
|
|
|
z |
|
|
|
|
|
|
Рис. 4.14. Деформации балок при изгибе |
|
|||
