Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

examples_of_typical_problems

.pdf

Скачиваний:

Добавлен:

29.03.2015

Размер:

1.92 Mб

Скачать

☆

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

ДЕЙСТВИЯ НАД МАТРИЦАМИ

1	0	3		1		1
Пример. Даны матрицы А = 2	4	1	, В =	3	, С =	2	и число = 2. Найти
1	4	2		2		1

АТВ+ С.
	1	2		1					1	2		1	1				1 1		2 3	1 2	9
AT = 0 4				4 ;			ATB = 0 4					4	3 = 0 1 4 3 4 2 = 4 ;
	3	1		2					3	1		2	2				3 1		1 3	2 2	10
				2									9				2		7
		C = 4 ;							АТВ+ С = 4 + 4 = 8 .
				2									10				2		12
												1
Пример. Найти произведение матриц А =												4	и В =		2		4	1 .
												3
				1					1 2		1 4		1 1			2		4	1
			АВ = 4 2 4 1 = 4 2 4 4 4 1													8 16 4 .
				3					3 2		3 4		3 1			6	12		3
							1
			ВА = 2		4	1	4	= 2 1 + 4 4 + 1 3 = 2 + 16 + 3 = 21.
							3
Пример. Найти произведение матриц А= 1												2	, В =		3		4
Пример. Найти произведение матриц А= 1												2	, В =		5		6
															5		6
				АВ =	1	2	3	4	=	3 10		4	12 =		13			16 .
							5	6
Пример. Дана матрица А =							3	2	, найти А3.
							1	4
А2 = АА =	3 2 3 2 =				11 14 ;					A3 =		3 2 11 14						=	47 78 .
	1	4	1	4	7	18						1	4	7		18			39	86
Отметим, что матрицы						3	2	и	11	14	являются перестановочными
						1	4		7	18

ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ

																														1			2	1
Пример. Вычислить определитель матрицы А =																														0			2	3
																														3			1	1
		2	1		2			3					0		3					0				2
	1
	1
	0	2	3	1							2					1										(			2 1				1 3)	2(0 1		3 3)		(0 1 3 2)
	3	1	1		1			1					3		1					3			1
	3	1	1
= -5 + 18 + 6 = 19.
		Пример:. Даны матрицы А =																				1		2 , В =						5			2 . Найти det (AB).
																						3		4						1			3
1-й способ: det A = 4 – 6 = -2;																		det B = 15 – 2 = 13;																det (AB) = det A det B = -26.
2- й способ: AB =								1 5				2 1			1 2				2				3			7				8			,	det (AB) = 7 18 - 8 19 = 126 –
2- й способ: AB =								3 5				4 1			3 2				4 3							19				18			,	det (AB) = 7 18 - 8 19 = 126 –
	– 152 = -26.
																						1		0					3	4
																						1		0					3	4
Пример.				Вычислить определитель																		2		1					1	2		.
																						0		3					2	1
																						2		1					4	3
								0				3			4							1		1		2					2		1	2		2	1	1
							1
							1
							2	1 1 2
							2	1 1 2								= -1					3 2 1						3				0 3 1				4	0 3 2
							0	3				2			1						1			4		3					2		1	3		2	1	4
							2	1				4			3						1			4		3					2		1	3		2	1	4
							2	1				4			3
								1			2
						1		1			2
						3		2			1	= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
						1		4			3
												1			2				0				2			1
									2			1			2				0				2			1
									0			3			1		=		0				3			1		= 2(0 – 2) – 1(0 – 6) = 2.
									2			1			3				2				1			3
											1	1						0	2					3
								2			1	1						0	2					3
								0		3		2		=				0	3					2	= 2(-4) – 3(-6) = -8 + 18 = 10.
								2		1		4						2	1					4

Значение определителя: -10 + 6 – 40 = -44.

ОПРЕДЕЛЕНИЕ РАНГА МАТРИЦЫ

Пример. Определить ранг матрицы.

1	0	0	0	5		1	0	0	0	5		1	5			1	5

0	0	0	0	0										,				11 10 1	0	RgA = 2.
						2	0	0	0	11		2	11			2	11
2	0	0	0	11
		Пример: Определить ранг матрицы.
3	5	7		4	8	12	1	2		3	1	2	3		1	2

1	2	3		1	2	3	1	2		3				,			3	2 1 0	Rg = 2.
1	3	5		1	3	5	1	3		5	1	3	5		1	3

Пример. Определить ранг матрицы.

1	2	1	3	4	1	2	1	3	4		1	2

3	4	2	6	8						,			4 6	2 0. Rg = 2.
1	2	1	3	4	3	4	2	6	8		3	4

РЕШЕНИЕ СИСТМЕ ЛИНЕЙНЫХ УРАВНЕНИЙ

Пример. Найти решение системы уравнений:

				5x	y	z	0
				x	2 y	3z	14
				4x	3y	2z	16
		1	1
	5	1	1
=	1	2	3	= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
	4	3	2

	0	1	1
1 =	14	2	3	= (28 – 48) – (42 – 32) = -20 – 10 = -30.
	16	3	2

x1 = 1/ = 1;

	5	0	1
2 =	1	14	3	= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
	4	16	2

x2 = 2/ = 2;

		5	1	0
3 =		1	2	14	= 5( 32 – 42)	+ (16 – 56) = -50 – 40 = -90.
		4	3	16
x3 = 3/ = 3.
Как видно, результат совпадает с результатом, полученным выше матричным
методом.
Если система	однородна,				т.е. bi = 0,	то при	0 система имеет единственное

нулевое решение x1 = x2 = … = xn = 0.

При = 0 система имеет бесконечное множество решений.

Для самостоятельного решения:

x 3y 6z 12

3x 2 y 5z 10;

Ответ: x = 0; y = 0; z = -2.

2x 5y 3z 6

Пример. Определить совместность системы линейных уравнений:


							x1		3x2		5x3			7x4		9x5	1
							x1		2x2		3x3			4x4		5x5	2
							2x1		11x2				12x3		25x4		22x5	4
			1	3	5	7		9		1			3		5	7	9	1	3	5	7	9
		A = 1		2 3		4 5 ~ 3						9 15 21 27 ~ 1							3 5 7 9 ~
			2	11	12	25	22			2			11		12	25	22	2	11	12	25	22
	1	3	5	7	9								3		1	6	5 0
	1	3	5	7	9						1		3
~	2	11	12	25	22 .						2		11					RgA = 2.
		1	3	5	7	9	1		1	3			5		7	9	1
A* =		1	2	3	4	5	2	~	0	0			0		0	0	1		RgA* = 3.
		2	11	12	25	22	4		2	11			12		25	22	4

Система несовместна.

Пример. Определить совместность системы линейных уравнений.

x1	4x2	1	1	4
3x1	2x2	4	3	2		1	4
3x1	2x2	4	3	2
7x1	10x2	12	А = 7	10	;			= 2 + 12 = 14 0; RgA = 2;
5x1	6x2	8	5	6		3	2
5x1	6x2	8	5	6
3x1	16x2	5	3	16

1	4	1		1	4		1	1	4	1
3	2	4		0	14		7	0	2	1		1	4	1
A* = 7	10 12 ~ 0 38 19							~ 0 2		1	~	1	4	1
5	6	8		0	26		13	0	2	1		0	2	1
5	6	8		0	26		13	0	2	1
3	16	5		0	4		2	0	2	1
				4		2	0.	RgA* = 2.
			1	4
			0	2
			0	2
Система совместна. Решения: x1 = 1;							x2 =1/2.

Пример. Решить систему линейных уравнений методом Гаусса.

2x1	x2	x3	5
x1	2x2	3x3	3
7x1	x2	x3	10

Составим расширенную матрицу системы.

2	1	1	5	1	2	3	3	1	2	3	3	1	2	3	3
А* = 1	2 3		3 ~ 2		1	1	5 ~ 0		5	7 11 ~ 0			5	7	11
7	1	1	10	7	1	1	10	0	15	22	31	0	0	1	2

Таким образом, исходная система может быть представлена в виде:

x1	2x2	3x3	3
5x2	7x3	11	, откуда получаем: x3 = 2; x2 = 5; x1 = 1.

x3 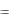2

Пример. Решить систему методом Гаусса.

5x y z 0

x 2 y 3z 14 4x 3y 2z 16

Составим расширенную матрицу системы.

5	1	1	0	1	2	3	14	1	2	3	14	1	2	3	14
1	2	3	14	~ 4	3	2	16	~ 0	5	10	40	~ 0	5 10		40
4	3	2	16	5	1	1	0	0	11	16	70	0	0	6	18

Таким образом, исходная система может быть представлена в виде:

x 2 y 3z 14

5y 10z 40 , откуда получаем: z = 3; y = 2; x = 1.

6z 18

Полученный ответ совпадает с ответом, полученным для данной системы методом Крамера и матричным методом.

Для самостоятельного решения:

x1	x2	x3	x4	4
2x1	x2	3x3	2x4		1
x1	x3	2x4	6		Ответ: {1, 2, 3, 4}.
x1	x3	2x4	6
3x1	x2	x3	x4	0

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

																																						2,								3,

				Пример. Найти (5 a											+ 3 b )(2 a - b ), если																					a						b					a	b.
																		= 10				2			3						2	40 27 13 ,
																						2									2
10 a a				- 5 a b + 6 a b - 3 b b																a								b
								2									2
								2									2
	т.к. a a					a			4, b b					b					9, a b 0 .

				Пример. Найти угол между векторами a и b , если a																																							i	2 j	3k ,

b			6i		4 j			2k .
Т.е.
Т.е.			a = (1, 2, 3),							b = (6, 4, -2)

a		b = 6 + 8 – 6 = 8:

			1		4		9		14;									36 16							4							56 .
	a		1		4		9		14;				b					36 16							4							56 .
cos			=		8						8							4			2		;											arccos						2	.
cos			=																				;											arccos							.
					14		56		2		14	14						14	7																7
				Пример.						Найти						скалярное											произведение																			-
				Пример.						Найти						скалярное											произведение														(3 a					-	2 b ) (5 a			- 6 b ), если
			4,				6,					/ 3.
	a		4,		b		6,		а^ b			/ 3.
																											2																			2				1
15 a			a	- 18 a				b - 10 a			b + 12 b							b	= 15					a							28		a	b			cos				12			b			15 16		28	4 6
15 a			a	- 18 a				b - 10 a			b + 12 b							b	= 15					a							28		a						3		12			b			15 16		28		2
+ 12 36 = 240 – 336 + 432 = 672 – 336 = 336.																																							3												2
+ 12 36 = 240 – 336 + 432 = 672 – 336 = 336.

				Пример. Найти угол между векторами a и b , если a																																							3i	4 j		5k ,

b			4i		5 j			3k .
Т.е.
Т.е.			a = (3, 4, 5),							b = (4, 5, -3)

a		b = 12 + 20 - 15 =17 :

	a		9		16		25		50;							b			16						25					9		50 .
cos			=		17				17		;								arccos							17			.
										50																50
					50		50
					50		50
																																																перпендикулярны.
				Пример. При каком m векторы a																										mi				j и b							3i				3 j		4k	перпендикулярны.

																		a = (m, 1, 0);															b = (3, -3, -4)

3 0;

1 .

a b

Пример. Найти скалярное произведение векторов 2a

и 5a

7c , если

3, a^ b a^ c b ^ c

( 2a 3b 4c )( 5a 6b 7c ) = 10a a 12a b 14a c 15a b 18b b 21b c

20c

24b

28c c

10 a

27a

34a

45b

18b

28c c = 10 +

+ 27 + 51 + 135 + 72 + 252 = 547.

ВЕКТОРОНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),

С(0, 1, 0).

					AC		(0			2;1	2;0		2)	( 2; 1;			2)
					AB		(4			2;0	2;3		2)	(2;		2;1)


							i			j		k		1		2		2	2		2		1
							i			j		k

	AC AB						2			1		2	i	2 1			j	2	1	k	2		2	i ( 1 4) j ( 2 4)
							2			2		1


	k (4				2)			5i		2 j		6k .

																			S			65	(ед2).
	AC			AB			25			4	36		65.									65
	AC			AB			25			4	36		65.								2
																					2
				Пример.					Доказать,				что векторы
				Пример.					Доказать,				что векторы					a	7i	3 j		2k ,	b	3i	7 j	8k	и c	i	j	k
компланарны.
					1		1			1		1	1	1
					3		7			8 ~		0	4		5 , т.к. векторы линейно зависимы, то они компланарны.
					7		3			2		0	4	5
				Пример.						Найти			площадь				параллелограмма,						построенного				на	векторах
														1;			300.

a		3b;			3a			b , если				a	b			a^ b

(a 3b) (3a b) 3a a a b 9b a 3b b																				b a 9b a 8b a
						sin 300				4 (ед2).
S		8	b		a	sin 300				4 (ед2).

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.

AB ( 2; 6;1)

Найдем координаты векторов: AC (4; 3; 2)

AD ( 4; 2;2)

Найдем смешанное произведение полученных векторов:

	2	6	1	2	6	1	0	6	1
AB AC AD	4	3	2	0	15	0	0	15	0	0 ,
	4	2	2	0	10	0	0	10	0

Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.

Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).

					BA	( 2;	3;		4)
Найдем координаты векторов: BD						(1;4;	3)
					BC	(4; 1; 2)
			1		3	4		1
				2	3	4
V				1	4	3			( 2( 8 3) 3( 2 12) 4( 1 16))
V		6		1	4	3	6		( 2( 8 3) 3( 2 12) 4( 1 16))
Объем пирамиды		6		4	1	2	6
Объем пирамиды				4	1	2
	1	(22		30	68)	20(ед3 )
6		(22		30	68)	20(ед3 )
6

Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.

ij k


	BD	BC			1			4	3	i (	8 3)		j ( 2		12) k (		1 16) 11i	10 j	17k .
					4			1	2

	BD	BC				112			102	172	121		100		289		510

Sосн =			510 / 2 (ед2)
Т.к. V =				S	осн		h	;	h	3V		120		4	510	. (ед)
					3					Sосн			17
											510
											510

УРАВНЕНИЯ ПЛОСКОСТИ

Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.


OP (4; 3;12);	OP	16 9 144 169 13

N (134 ; 133 ;1213)

Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой:

A(x – x0) + B(y – y0) + C(z – z0) = 0.

4		(x	4)				3		( y		3)	12			(z	12)	0

13						13						13
13						13						13
	4	x	16			3			y		9		12	z		144	0

13			13			13					13	13				13
13			13			13					13	13				13
	4	x		3	y			12		z	169				0

13			13			13					13
13			13			13					13
4x			3y		12z				169			0.

Пример. Найти уравнение плоскости, проходящей через две точки P(2; 0; -1) и Q(1; -1; 3) перпендикулярно плоскости 3х + 2у – z + 5 = 0.

Вектор нормали к плоскости 3х + 2у – z + 5 = 0 N (3;2; 1) параллелен искомой

плоскости. Получаем:

	x	2	y	0	z		1
	1	2	1	0	3		1	0
		3	2				1
	x	2	y	z	1
	x	2	y	z	1
		1	1	4			0
		3	2	1
(x		2)(1		8) y(1			12)		(z 1)( 2 3) 0
	7(x		2)	11y		(z		1)	0
	7x		14	11y		z	1		0
	7x		11y	z	15		0

Пример. Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2z – 3 = 0.

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.2016356.48 Кб17ELSnabStroiPl_Kursovoi(1).pdf
#
12.03.2016690.29 Кб39EN 1990.2002 Basis of structural design.pdf
#
29.03.201563.65 Кб115energetika__33__33__33_-_kopia.docx
#
29.03.2015431.06 Кб9english.docx
#
07.09.2019372.19 Кб2Erica Lawson - Possessing Morgan.docx
#
29.03.20151.92 Mб9examples_of_typical_problems.pdf
#
28.03.2015159.74 Кб25ExceLab1.doc
#
29.03.2015241.66 Кб21ExceLab1.doc
#
28.03.201563.49 Кб17ExceLab2.doc
#
29.03.2015248.83 Кб16ExceLab2.doc
#
29.03.2015492.03 Кб29ExceLab3.doc

4		(x	4)				3		( y		3)	12			(z	12)	0

13						13						13
13						13						13
	4	x	16			3			y		9		12	z		144	0

13			13			13					13	13				13
13			13			13					13	13				13
	4	x		3	y			12		z	169				0

13			13			13					13
13			13			13					13
4x			3y		12z				169			0.

4		(x	4)				3		( y		3)	12			(z	12)	0

13						13						13
13						13						13
	4	x	16			3			y		9		12	z		144	0

13			13			13					13	13				13
13			13			13					13	13				13
	4	x		3	y			12		z	169				0

13			13			13					13
13			13			13					13
4x			3y		12z				169			0.

4		(x	4)				3		( y		3)	12			(z	12)	0

13						13						13
13						13						13
	4	x	16			3			y		9		12	z		144	0

13			13			13					13	13				13
13			13			13					13	13				13
	4	x		3	y			12		z	169				0

13			13			13					13
13			13			13					13
4x			3y		12z				169			0.