
examples_of_typical_problems
.pdf
Второй способ решения того же самого примера.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
tgt |
|
|
|
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
dx |
|
|
|
|
x |
|
|
|
|
; dx |
dt; |
|
|
|
|
|
|
|
|
sin t cos 4 t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2 t |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos t |
cos t |
|
dt |
|
dt |
cos |
tdt |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
cos |
2 |
t sin t |
|
|
|
||||||||||||||||||||||
|
x |
3 |
|
x |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x 2 |
|
|
1 |
|
|
|
tgt; |
|
|
|
|
|
tgt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos3 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
1 |
|
cos 2t dt |
|
1 |
t |
|
1 |
sin 2t |
sin 2t |
2 sin t cos t |
2 |
1 |
|
|
|
|
x 2 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
2 |
4 |
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
arccos |
1 |
|
|
|
x 2 |
|
|
1 |
|
|
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
x |
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
С учетом того, что функции arcsin и arccos связаны соотношением |
arcsin |
1 |
|
|
|
|
arccos |
1 |
, |
||||||||||||||||||||||||||||||||||||||||||||
x |
|
2 |
x |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а постоянная интегрирования С – произвольное число, ответы, полученные различными методами, совпадают.
Как видно, при интегрировании иррациональных функций возможно применять различные рассмотренные выше приемы. Выбор метода интегрирования обуславливается в основном наибольшим удобством, очевидностью применения того или иного метода, а
также сложностью вычислений и преобразований. |
|
|
|
|
||||||||||||
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
x |
sin t; |
|
cos tdt |
|
dt |
|
|
|
x |
|
|
|||
|
dx |
|
cos tdt; |
|
|
|
tgt C |
|
|
C. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(1 x 2 )3 / 2 |
|
|
cos3 t |
|
cos 2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
t |
1 x2 |
|
|
||||||
|
cos t |
1 x2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пример.
1 |
|
|
|
x sint; |
|
/ 2 |
|
|
|
/ 2 |
1 |
/ 2 |
|
|
|
|
|
|
|
||||||
1 |
x2 dx |
0; |
/ 2 |
|
1 sin2 t costdt |
cos2 tdt |
|
(1 cos2t)dt |
||||
|
2 |
|||||||||||
0 |
|
|
|
0 |
|
|
|
0 |
0 |
|||
1 |
t |
1 |
sin 2t |
|
2 |
2 |
|||
|
|
/ 2 |
|
|
1 |
|
|
|
|
|
|
sin |
|
. |
|
|
4 |
4 |
4 |
|||
0 |
|
|
||||
При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.
51
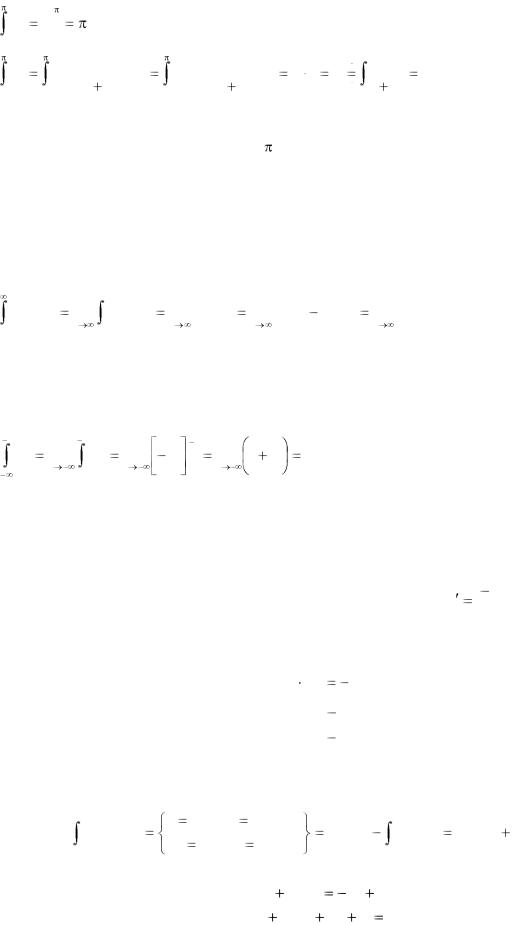
Пример. |
|
|
|
|
|
|
|
|
|
|||
dx |
x |
|
|
, с другой стороны, если применить тригонометрическую подстановку, |
||||||||
|
|
|||||||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
dx |
|
0 |
|
dt |
|
dx |
|
|
|
|
|
tgx t |
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|
|||
|
sin 2 |
x cos 2 x |
|
cos 2 |
x(1 tg 2 x) |
|
1 t 2 |
|||||
0 |
0 |
0 |
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||
Т.е. два способа нахождения интеграла дают различные результаты. Это произошло из -за того, что не был учтен тот факт, что введенная переменная tgx имеет на отрезке интегрирования разрыв (в точке х = /2). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Пример.
b |
b |
|
cos xdx |
lim cos xdx |
lim sin x |
|
lim (sin b sin 0) lim sin b - не существует. |
||||||||||||
0 |
|
|
|
b |
|
0 |
|
b |
|
|
0 |
b |
|
b |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Несобственный интеграл расходится. |
|
|
||||||||||||||
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|||
1 |
dx |
|
1 |
dx |
|
1 |
1 |
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
lim |
|
lim |
|
|
lim |
1 |
1 - интеграл сходится |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
||||||
|
x |
b |
b |
x |
b |
|
x b |
b |
|
b |
|
|||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Пример. Найти общее решение дифференциального уравнения: |
yy |
2x |
|||
|
|||||
cosy |
|||||
|
|
|
|
||
y cos y |
dy |
2x |
|
|
|
dx |
|
|
|||
|
|
|
|
||
y cos ydy 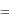 2xdx
2xdx  y cos ydy
y cos ydy 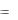 2
2 xdx
xdx
Интеграл, стоящий в левой части, берется по частям (см. Интегрирование по частям.):
y cos ydy |
u |
y; dv |
cos ydy; |
y sin y |
sin ydy y sin y cos y |
||
du |
dy; v |
sin |
y |
||||
|
|
|
|||||
|
|
y sin y |
cos y |
x2 |
C |
||
y sin y cos y x2 C 0
52

-это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.
y sin y yy cos y y sin y 2x 0
2x
yy cos y - верно
Пример. Найти решение дифференциального уравнения |
y |
ln y при условии у(2) |
|
|
|||
y |
|||
|
|
= 1.
ydx ln y dy
dx |
ln ydy |
||
|
|
|
|
|
y |
||
|
|
||
dx |
|
ln ydy |
|
|
|
|
|
|
y |
||
|
|
||
x C 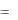 ln yd (ln y)
ln yd (ln y)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x C |
|
ln 2 y |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
при у(2) = 1 получаем 2 |
|
C |
|
|
|
ln 2 1 |
; |
|
|
|
2 |
|
|
C |
|
0; |
|
C |
2; |
||||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итого: 2(x 2) |
ln2 |
y; |
или y e |
|
2 x 4 |
- частное решение; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка: |
y |
|
e |
|
2 x |
4 |
|
|
|
|
|
|
|
|
, итого |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
2x |
4 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y |
|
|
e |
|
|
2 x 4 ( |
|
|
2x |
4) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 4 |
ln y - верно. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y |
|
|
|
|
|
|
e |
2 x 4 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Решить уравнение y |
y 2 3 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
y |
2 |
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 23 dy |
|
dx |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2 3 dy |
|
|
dx |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3y 13 |
|
x |
|
|
C |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27y |
(x |
C)3 - общий интеграл |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
1 |
|
|
(x |
|
C)3 - общее решение |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример. Решить уравнение y |
x( y2 |
|
1). |
|
|
|
|
|
|||||||||||||||||||||||
53

|
dy |
|
|
|
|
|
dx; |
|
|
dy |
dx; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y 2 |
|
1 |
|
y 2 |
|
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
x2 |
||||
arctgy |
|
|
|
|
|
|
|
C; |
|
y |
|
tg |
|
C ; |
||||
|
2 |
|
|
|
|
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Решить уравнение |
|
yy |
|
e y |
0 при условии у(1) = 0. |
|||||||||||||
|
x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
ydy |
xe y |
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ydy |
xey dx |
0; |
|
|
y |
|
dy |
|
xdx; |
|||||||||
|
|
e y |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
eyy dy  xdx;
xdx;
Интеграл, стоящий в левой части будем брать по частям (см. Интегрирование по частям. ).
ye y dy |
u |
y; e y dy |
dv; |
e y y |
e y dy |
e y y |
e y |
e y ( y 1); |
|||||
du |
dy; v |
e y ; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
e y ( y |
1) |
x 2 |
C |
|
; |
|
|
||
|
|
|
|
2 |
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2e y ( y |
1) x2 |
C |
|
|
|||||
Если у(1) = 0, то 2e0 (0 1) 1 C; |
|
2 |
|
1 C; |
C |
1; |
|||||||
Итого, частный интеграл: 2e y ( y 1) x2 1.
Пример. Решить уравнение y |
sin(x |
|
y) sin(x y) . |
|
||||||||
|
|
y sin(x |
y) |
|
sin(x |
y) |
0 |
|
||||
|
y 2 sin |
x |
y |
x |
y |
cos |
x |
y x |
y |
0 |
||
|
2 |
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y |
2sin( |
y) cosx |
0 |
|
|
||||
|
|
|
y |
|
2sin y cosx |
0 |
|
|
||||
|
dy |
2 cos xdx; |
|
|
dy |
2 |
cos xdx; |
|||||
|
|
|
|
|
|
|||||||
|
sin y |
|
|
sin y |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Для нахождения интеграла, стоящего в левой части уравнения см. Таблица основных интегралов. п.16. Получаем общий интеграл:
ln |
tg |
y |
2sin x C |
|
|||
|
2 |
|
|
54

Пример. Решить уравнение 2xe x |
2 |
|
|
|
y |
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем заданное уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2xe x |
2 |
|
|
|
dy |
0 |
||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
ydx |
||||||||||
|
|
|
|
|
|
|
|
|
||||||
2xe x |
2 |
dx |
|
|
|
dy |
0 |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
2xe x |
2 |
dx |
|
|
|
|
dy |
C |
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
y |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
e x2 |
|
|
|
|
||||||||||
|
|
ln |
y |
C |
||||||||||
Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.
Пример. Решить уравнение y |
|
x( y2 |
1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dy |
|
x( y |
2 |
|
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
y 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dy |
|
|
|
xdx; |
|
|
|
|
|
arctgy |
|
x 2 |
|
C |
; |
|
|
|||||||||||||||
|
|
|
y 2 |
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
y tg |
x 2 |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Допустим, заданы некоторые начальные условия х0 и у0. Тогда: |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
arctgy |
|
|
|
0 |
|
C |
|
; |
|
|
|
|
|
C |
|
|
|
arctgy |
|
|
|
|
0 |
; |
|
|||||||||
0 |
|
|
2 |
|
0 |
|
|
|
|
|
0 |
|
0 |
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Получаем частное решение y |
|
tg |
|
x2 |
|
|
arctgy |
|
|
|
x02 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Решить уравнение (x |
|
2y |
|
3)dy |
(2x |
|
y |
|
1)dx |
0. |
|
|
|
|
|
|
|||||||||||||||||||
Получаем (x 2 y 3) |
dy |
|
2x |
y |
1; |
|
|
|
|
|
dy |
|
|
|
|
|
2x |
|
y |
1 |
; |
|
|
|
|
|
|
|
|||||||
dx |
|
|
|
|
|
dx |
|
|
|
|
x |
|
2 y |
3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Находим значение определителя |
|
|
2 |
|
|
|
1 |
|
4 |
|
1 |
|
|
5 |
|
0 . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решаем систему уравнений |
|
|
2x |
|
y |
1 |
|
|
0; |
|
|
|
|
y |
|
1 |
|
2x |
|
|
|
|
|
; |
|
x |
1/ 5; |
||||||||
|
|
|
x 2 y 3 0 |
|
|
|
|
|
x 2 4x 3 0 |
|
y 7 / 5 |
||||||||||||||||||||||||
Применяем подстановку x |
u |
|
1/ 5; |
|
y |
|
|
v |
|
7 / 5; в исходное уравнение: |
|||||||||||||||||||||||||
55

(u 1/ 5 2v |
14/ 5 3)dv (2u |
2 / 5 |
|
|
v |
7 / 5 |
1)du 0; |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(u 2v)dv (2u |
v)du |
|
|
0; |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dv |
|
|
2u |
v |
|
|
|
|
2 v / u |
; |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
2v |
u |
|
|
|
2v / u |
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Заменяем переменную |
|
v |
|
|
|
|
t; v |
|
|
|
|
ut; |
|
v |
|
t u |
|
t; |
|
при |
подстановке в выражение, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
u |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
записанное выше, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t u |
t |
2 |
|
t |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Разделяем переменные: |
dt |
|
u |
|
2 |
|
|
|
t |
|
t |
|
2 |
|
|
|
t |
2t 2 |
t |
|
|
2(1 |
t |
t 2 ) |
; |
||||||||||||||||||
du |
|
2t |
1 |
|
|
|
|
|
|
|
2t |
1 |
|
|
|
|
|
|
|
2t |
1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
du |
|
|
|
|
1 |
|
1 |
|
|
2t |
|
|
|
dt; |
|
|
|
|
du |
|
|
|
1 |
|
|
(1 2t)dt |
; |
|
||||||||||||||
|
|
|
|
|
|
2 1 t t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
2 1 t t 2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
ln |
1 |
|
|
|
t |
|
|
|
ln |
u |
|
ln C |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln |
1 |
|
|
t |
|
|
|
|
|
|
2 ln |
C u |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
C2 |
|
; 1 t t 2 |
C2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
ln |
|
1 t t 2 |
|
|
|
|
ln |
|
; |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
u 2 |
u 2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Переходим теперь к первоначальной функции у и переменной х.
t |
|
v |
|
|
y 7 / 5 5 y 7 |
; u x 1/ 5; |
||||||||
|
u |
|
|
x |
1/ 5 |
|
|
5x |
1 |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
5y |
7 |
|
|
5y 7 |
2 |
|
25C2 |
; |
|||
|
|
5x 1 |
|
5x 1 |
|
|
(5x 1)2 |
|||||||
|
(5x |
1)2 |
(5y |
7)(5x |
1) (5y |
7) |
2 |
|
25C |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25x2 |
10x |
|
1 25xy |
5y |
35x |
7 |
25y2 |
|
70y |
49 25C |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
25x2 |
|
25x |
25xy |
75y |
25y2 |
25C |
2 |
49 |
1 |
7 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x 2 |
x xy 3y y 2 |
C |
|
55 |
|
|
C; |
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итого, выражение |
x2 |
x |
xy |
3y |
y2 |
C |
|
является |
|
общим |
|
интегралом исходного |
|||||||||||
дифференциального уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В случае если |
в исходном |
уравнении |
вида |
y |
|
f |
|
ax |
|
by |
c |
|
|
определитель |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
a1 x |
|
|
b1 y |
c1 |
|||||||||||||||||
a b
0, то переменные могут быть разделены подстановкой
a1 b1
ax by t.
56

Пример. Решить уравнение 2(x |
|
|
y)dy |
(3x |
3y |
1)dx |
0. |
|
|
|
||||||||||||||||||||||||||
Получаем 2(x |
|
y) |
dy |
|
3x |
3y |
1; |
|
dy |
|
|
|
|
|
3x 3y 1 |
3x |
3y |
1 |
; |
|||||||||||||||||
|
dx |
|
|
dx |
|
|
|
|
|
2x |
2 y |
|
|
2x |
2 y |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Находим значение определителя |
|
3 |
3 |
|
|
6 |
6 |
|
|
0; |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Применяем подстановку 3x |
3y |
t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
t |
1; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
3 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставляем это выражение в исходное уравнение: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
t |
|
1 |
|
|
3(t |
1) |
; 2t(t |
3) |
|
|
9t |
|
|
|
9; 2tt |
|
6t |
|
9t |
9; 2tt |
|
3t 9; |
|||||||||||||
3 |
|
|
|
|
2t |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разделяем переменные: |
|
2t |
|
dt |
dx; |
|
|
|
|
|
|
|
|
t |
|
dt |
|
3 |
dx; |
|
|
|
|
|||||||||||||
3t |
9 |
|
|
|
|
|
|
t |
3 |
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
dt |
|
3 |
dx; |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t 3 |
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t 3ln |
t |
3 |
|
|
|
C |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Далее возвращаемся к первоначальной функции у и переменной х.
2x 2 y 2 ln |
3(x y 1) |
x C2 ; |
3x 2 y 2 ln 3 2 ln x y 1 C2 ; 3x 2 y 2 ln x y 1 C;
таким образом, мы получили общий интеграл исходного дифференциального уравнения.
Пример. Решить уравнение xy |
|
y |
xy2 ln x. |
|
|
|
|
||||||||||
Разделим уравнение на xy2: |
y |
|
1 |
|
1 |
ln x. |
|
|
|
|
|||||||
y 2 |
|
x |
y |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Полагаем z |
1 |
; |
|
z |
y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y |
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
1 |
z ln x; |
z |
1 |
z |
ln x . |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
||
Полагаем P |
|
1 |
, |
Q |
ln x. |
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
dx |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
eln x |
ln xe ln x dx C ; |
z e |
x |
ln xe |
|
x dx |
C ; |
z |
||||||
z |
|
x |
ln x |
dx |
C ; |
z |
x |
ln xd(ln x) C ; |
||||
|
|
x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
z |
x |
ln 2 x |
C |
|
||
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Произведя обратную подстановку, получаем:
1 |
x |
ln 2 x |
C . |
|
y |
2 |
|||
|
|
57

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|||||
Пример. Решить уравнение xy |
|
4 y |
|
y. |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разделим обе части уравнения на x |
y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
dy |
4 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
x. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y dx |
x |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагаем z |
y; z |
|
|
|
y ; y |
2 |
|
|
|
|
y z ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
4 |
z x; |
|
|
dz 2z |
|
x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 y z |
|
|
|
; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
x |
|
|
|
|
dx |
|
x |
2 |
|
||||||||||
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
dz |
|
2z |
0; |
dz |
|
2z |
; |
dz |
|
2dx |
; |
dx |
|
x |
dx |
|
x |
z |
|
x |
|||
|
|
|
|
|
|
dz |
2 |
dx |
C ; ln z 2 ln x |
|
|
||
z |
|
x |
1 |
|
|
Полагаем C = C(x) и подставляем полученный уравнение, с учетом того, что:
ln C; z Cx 2 ;
результат в линейное неоднородное
|
dz |
|
2xC(x) x |
2 |
dC(x) |
; |
|
|
||||||||
|
dx |
|
|
|
dx |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2xC(x) x |
2 dC(x) 2x2C(x) |
x |
; |
|||||||||||||
|
|
dx |
|
|
|
x |
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dC(x) |
|
|
1 |
|
; |
C(x) |
|
1 |
ln x C2 ; |
|||||||
dx |
|
|
|
2 |
||||||||||||
|
2x |
|
|
|
|
|
|
|
|
|||||||
Получаем: z x2 C |
|
1 |
ln x ; |
|
2 |
2 |
|||
|
|
|||
|
|
|
Применяя обратную подстановку, получаем окончательный ответ:
|
|
2 |
||
y x4 C |
|
1 |
ln x ; |
|
2 |
2 |
|||
|
|
|||
|
|
|
||
Пример. Решить уравнение с заданными начальными условиями.
y |
y |
x 1; y(1) 0. |
|
|
|||
x |
|||
|
|
Это линейное неоднородное дифференциальное уравнение первого порядка. Решим соответствующее ему однородное уравнение.
y |
y |
0; |
y |
|
y |
; |
|
dy |
|
y |
; |
|
dy |
|
dx |
; |
||
x |
|
x |
|
dx |
|
x |
|
y |
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dy |
|
dx |
; |
|
|
ln y |
ln x |
|
ln C; |
|
|
|
|||
|
|
|
y |
|
x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
y |
Cx; |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
58 |
|
|
|
|
|
|
|
|
|
Для неоднородного уравнения общее решение имеет вид: y C(x)x;
Дифференцируя, получаем: y C (x)x C(x);
C (x)x C(x);
Для нахождения функции С(х) подставляем полученное значение в исходное дифференциальное уравнение:
|
|
|
|
|
C (x)x C(x) C(x) x 1 |
|||||||||
|
|
|
|
|
|
|
|
xC (x) x |
1 |
|
|
|||
|
|
|
C (x) 1 |
1 |
; |
|
C(x) |
1 |
1 |
dx C; |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
C(x) |
|
x ln x |
C; |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Итого, общее решение: |
y |
x(x |
ln x |
C). |
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||
C учетом начального условия |
y(1) |
|
0 определяем постоянный коэффициент C. |
|||||||||||
|
|
|
|
|
0 |
1 |
ln1 C; |
C |
1. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Окончательно получаем: |
|
y |
x2 |
x ln x |
x. |
|
|
|
|
|||||
Для проверки подставим полученный результат в исходное дифференциальное уравнение:
2x ln x x |
1 |
1 x ln x 1 x 1; верно |
|
x |
|||
|
|
Ниже показан график интегральной кривой уравнения.
1.5
1
0. |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. 5 |
|
|
|
1 |
|
|
1. 5 |
2 |
|
|||
- 0. |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Найти общий интеграл уравнения x( y2 |
1)dx |
y(x2 1)dy 0 . |
||||||||||||||||||
Это уравнение с разделяющимися переменными. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
xdx |
ydy |
0; |
|
|
|
xdx |
|
ydy |
; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x2 |
|
1 y 2 1 |
|
|
|
|
x2 1 |
|
y 2 |
1 |
|
||||||||
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
ln |
x2 |
1 |
ln |
|
1 |
ln C; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий интеграл имеет вид: |
(x2 |
1)(y2 |
|
1) C. |
|
|
|
|
|
|
|
|
|
|||||||
Построим интегральные кривые дифференциального уравнения при различных значениях С.
59

С = - 0,5 |
|
|
|
|
|
С = -0,02 |
|
|
С = -1 |
С = -2 |
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1. 5 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0. 5 |
|
|
|
|
- 2 |
|
|
|
- 1 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
- 0. 5 |
|
|
|
|
|
|
|
|
|
|
|
|
- 1 |
|
|
|
|
|
|
|
|
|
|
|
|
- 1. 5 |
|
|
|
|
|
|
|
|
|
|
|
|
- 2 |
|
|
|
|
С = 0,02 |
|
|
|
|
|
С = 0,5 |
|
С = 1 |
|
|
С = 2 |
|
Пример. Найти решение дифференциального уравнения, удовлетворяющее |
||||||||||||
заданным начальным условиям. |
|
|
|
|
|
|
|
|
|
|
||
|
y cosx |
( y |
1)sin x; |
y(0) |
0. |
|
||||||
Это уравнение с разделяющимися переменными. |
|
|
|
|
||||||||
|
|
|
y |
|
sin x ; |
dy |
tgxdx; |
|
|
|
||
|
|
y |
1 |
|
cos x |
y |
1 |
|
|
|
|
|
dy |
|
|
tgxdx; |
|
ln y |
|
1 |
ln cos x |
ln C; |
|
||
y |
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
ln ( y |
1) cos x |
|
ln C; |
|
( y |
1) cos x |
C; |
|
||||
Общее решение имеет вид: |
y |
|
C |
|
1. |
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
Найдем частное решение при заданном начальном условии у(0) = 0.
0 |
С |
1; C 1. |
|
|
|||
1 |
|||
|
|
1
Окончательно получаем: y 1. cos x
60
