Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

examples_of_typical_problems

.pdf

Скачиваний:

Добавлен:

29.03.2015

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Пример. Решить предыдущий пример другим способом.

Действительно, уравнение y cosx	( y	1) sin x может быть рассмотрено как
линейное неоднородное дифференциальное уравнение.
y cosx	y sin x	sin x.

Решим соответствующее ему линейное однородное уравнение.

y cos x y sin x 0;

y cos x y sin x;

tgxdx;

tgxdx ln C;

cos x

ln C;

y cos x C;

cos x

Решение неоднородного уравнения будет иметь вид: y

C(x)

cos x

Тогда y

C (x) cos x C(x) sin x

cos 2 x

Подставляя в исходное уравнение, получаем:

C (x) cos x

C(x) sin x cos x

C(x) sin x

sin x;

cos 2 x

cos x

C (x) cos x

sin x;

C x)

sin x;

C(x)

sin xdx

cos x C;

cos x

Итого y

cos x C

;

cos x

С учетом начального условия у(0) = 0 получаем y 1; cos x

Как видно результаты, полученные при решении данного дифференциального уравнения различными способами, совпадают.

При решении дифференциальных уравнений бывает возможно выбирать метод решения, исходя из сложности преобразований.

Пример. Решить уравнение y y cos x	1	sin 2x с начальным условием у(0) = 0.
	2

Это линейное неоднородное уравнение. Решим соответствующее ему однородное уравнение.

y y cos x 0;		dy	cos xdx;		ln	y	sin x C1 ;


		y

y	e sin x eC1 ;			y	Ce sin x ;

Для линейного неоднородного уравнения общее решение будет иметь вид:

y C(x)e sin x ;

Для определения функции С(х) найдем производную функции у и подставим ее в исходное дифференциальное уравнение.

			y	C (x)e sin x		C(x)e sin x cosx;
		C (x)e sin x C(x)e sin x cosx C(x)e sin x cosx sin x cosx;
		C (x)e sin x		sin x cosx;		C (x)		esin x sin x cosx;
С(x)	esin x sin x cosxdx		V	esin x ;	dU		cosxdx;		esin x sin x esin x cosxdx
С(x)	esin x sin x cosxdx		dV	esin x cosxdx;			U sin x;		esin x sin x esin x cosxdx
			dV	esin x cosxdx;			U sin x;
esin x sin x	esin x	C.
Итого y		e sin x esin x sin x		esin x C ;		y	sin x	1 Ce sin x ;

Проверим полученное общее решение подстановкой в исходное дифференциальное уравнение.

cosx Ce sin x ( cosx) sin x cosx cosx Ce sin x cosx sin x cosx; (верно)

Найдем частное решение при у(0) = 0.

0 sin0 1 Ce0 ;

C 1.

Окончательно y sin x e sin x 1.

Пример. Найти решение дифференциального уравнения

20xdx 3ydy 3x2 ydy 5xy2 dx

с начальным условием у(1) = 1.

Это уравнение может быть преобразовано и представлено как уравнение с разделенными переменными.

20x

3yy

3x2 yy

5xy2 ;

3yy (x2

5x( y2 4);

;

dx;

y 2

4 x2

y 2 4

dx;

y 2

ln( y 2

ln( x 2

ln C

( y 2

4)3

C (x2

1)5 ;

y 2

4 C 3 (x2 1)2 ;

y 2

C(x2

1) 3

C(x2

1) 3

С учетом начального условия:

5		125

1 С 2 3	4 С3 32 4; 1 2C3 4 4; 5 2C3 4; 125 8C 3 4; C 3			;
1 С 2 3	4 С3 32 4; 1 2C3 4 4; 5 2C3 4; 125 8C 3 4; C 3		32	;
			32

						C	5		.
							23
								4
								4


					5
Окончательно			x 2	1	3
	y	5			4.
	y	5		2	4.
				2

Пример. Решить дифференциальное уравнение xy y x 1 с начальным условием у(1) = 0.

Это линейное неоднородное уравнение.

Решим соответствующее ему однородное уравнение.

xdy

xy y 0;

;

ln C;

xy C;

;

Решение неоднородного уравнения будет иметь вид:

yC(x) ; x

Подставим в исходное уравнение:

C (x)x C(x)

C(x)

x 1;

C (x)x

x 1;

C (x) x 1;

x 2

C(x)

x 2

Общее решение будет иметь вид:

;

C учетом начального условия у(1) = 0: 0

;

Частное решение:

2 2x

Пример. Найти решение дифференциального уравнения xy

y ln

с начальным

условием у(1) = е.

Это уравнение может быть приведено к виду уравнения с разделяющимися

переменными с помощью замены переменных.

Обозначим: ln

eu ;

xeu ;

xu eu

eu ;

Уравнение принимает вид:

xu eu

eu u;

xu 1 u;

xu u 1;

Получили уравнение с разделяющимися переменными.

;

ln C;

Cx;

u 1

eCx 1 ;

Сделаем обратную замену: Cx

Общее решение:

xeCx 1;

eC 1;

C учетом начального условия у(1) = е:

Частное решение:

ex;

Второй способ решения.

y ln

;

y ln y

y ln x;

ln y

ln x;

Получили

линейное

неоднородное

дифференциальное

уравнение.

Соответствующее однородное:

ln y

ln y;

;

d ln

;

y ln y

ln y

eCx ;

ln y

ln C;

ln y

Cx;

Решение исходного уравнения ищем в виде:

eC( x) x ;

Тогда y eC( x) x C (x)x C(x) ;

Подставим полученные результаты в исходное уравнение:

xeC ( x) x C (x)x C(x) eC ( x) x ln

eC ( x) x

;

x 2C (x)

xC(x)

C(x)x ln x;

x 2C (x)

ln x;

C (x)

ln x

;

x 2

ln x;

;

ln x

x 2

ln x

C(x)

x 2

; v

;

y eC( x) x

eln x 1 Cx xeCx 1;

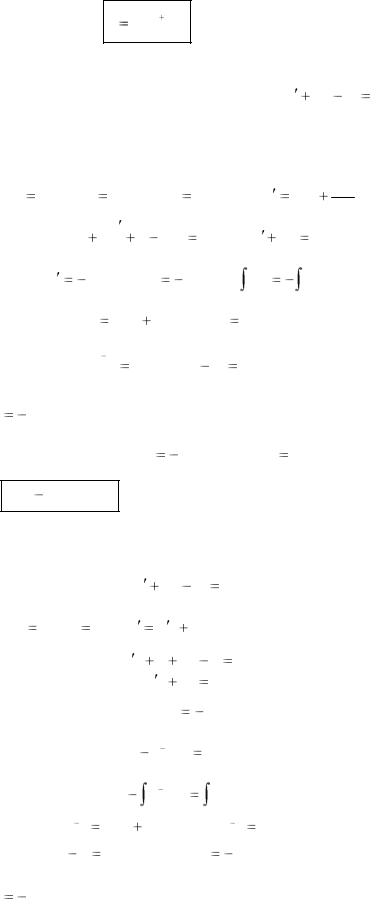
Получаем общее решение: y xeCx 1;

Пример.

Решить дифференциальное

уравнение

e x

условием у(1)=0.

В этом уравнении также удобно применить замену переменных.

e x

lnu;

y x lnu;

y lnu

Уравнение принимает вид: ln u

ln u

u 2

u 2 ;

;

u 2

ln C;

ln Cx;

Делаем обратную подстановку:

e x

lnCx;

ln(lnCx);

Общее решение:

x ln(lnCx);

y	0	с начальным

x
x

xuu ;

C учетом начального условия у(1) = 0: 0

ln(lnC);

C e;

Частное решение: y 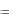x ln(lnex);

Второй способ решения.

e x

Замена переменной: u

;

ux; y

u x

e u du

;

e u

e u ln

;

ln C;

ln(ln

);

ln(ln

);

Общее решение:

x ln(lnCx);

Пример. Решить уравнение y

0 .

Составим характеристическое уравнение:

k 3

(k 1)(k 2

k 2 k

D 1 4

C e x

x .

Общее решение имеет вид:

e 2

cos

sin

Пример. Решить уравнение (1 x2 ) y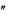 2xy 2y 0.

Это линейное однородное дифференциальное уравнение с переменными коэффициентами второго порядка. Для нахождения общего решения необходимо отыскать какое - либо частное решение.

Таким частным решением будет являться функция y1 x.

y1 1; y1 0;

0 2x 2x 0;

Исходное дифференциальное уравнение можно преобразовать:

y	2x	y	2 y	0.

	1 x 2		1 x 2

Общее решение имеет вид: y

	y C1 x	dx

		x 2 (1 x 2 )
		x 2 (1 x 2 )

2 x

C x

e 1

C x

e ln(1 x2 )

C2 x;

y C2 x C1 x

dx;

x 2

2(1 x)

1 x

y C

x C x

;

Окончательно:					1	x
	y C2 x		C3 x ln		1	x		C4 ;
	y C2 x		C3 x ln	1		x		C4 ;
				1		x

Пример. Решить уравнение y IV								y		0.
Составим характеристическое уравнение: k 4											1		0.
	(k 2 1)(k 2 1)					0;		k		1;	k	2			1; k	3	i; k	4	i.
								1				2				3		4

Общее решение:		y	C ex			C	e	x C	3	cos x			C	4	sin x.
			1			2			3					4
										66

Пример. Решить уравнение y

Характеристическое уравнение:

k 2

Общее решение:

C e2x

xe2x .

Пример. Решить уравнение y

Характеристическое уравнение:

k 2

16;

2i;

2i.

Общее решение:

e x (C cos2x

sin2x).

Пример. Решить уравнение y

7 y 6 y 0.

Характеристическое уравнение:

k 3

7k 2

k(k 2

k 3

Общее решение:

e x

e6 x ;

Пример. Решить уравнение y

Характеристическое уравнение:

k 2

1; k

Общее решение:

C e x

e2x .

Пример. Решить уравнение yV

Характеристическое уравнение:

k 5

9k 3

k 3 (k 2 9)

Общее решение:

x C

e3x

e 3x ;

Пример. Решить уравнение yy

y 2

Это уравнение не является линейным, следовательно, приведенный выше метод

решения к нему неприменим.

Понизим порядок уравнения с помощью подстановки y

Тогда y

p p 2

0; p 0; y C ;

ydp

;

ln C;

Cy;

dx;

Сy

x ln C2 ;

Cy e

C ln C2

C3e

;

Окончательно получаем:

y C eCx ;

Это выражение будет общим решением исходного дифференциального уравнения. Полученное выше решение у1 = С1 получается из общего решения при С = 0.

Пример. Решить уравнение 3yy

y 2

Производим замену переменной: y

;

3yp

p 2

;

ln C;

;

y C y 3

;

y 3 dy C dx;

3 C x C

;

y 3

;

Общее решение:

y (C

x C

) 4 .

Пример. Решить уравнение y y x sin 2x.

Правую часть дифференциального уравнения представим в виде суммы двух функций f1(x) + f2(x) = x + (-sinx).

Составим и решим характеристическое уравнение: k 2 1 0;						k	1,2	i;
							1,2
1. Для функции f1(x) решение ищем в виде y				xr e xQ(x) .
			1
Получаем:	0, r 0, Q(x) Ax	B; Т.е.	y1	Ax	B;
	y1	A;	y1	0;
	Ax	B x;	A	1; B	0;

Итого:

2. Для функции f2(x) решение ищем в виде:

xr e x (Q (x) cos

Q (x)sin x) .

Анализируя функцию f2(x), получаем: P1 (x)

P2 (x)

2; r 0;

Таким образом, y2

C cos 2x

D sin 2x;

2C sin 2x

2D cos 2x;

4C2 cos x

4D sin 2x;

4C cos 2x

4D sin 2x

C cos 2x

D sin 2x

sin 2x;

3C cos 2x

3D sin 2x

sin 2x

;

Итого:

sin 2x;

Т.е. искомое частное решение имеет вид:

sin 2x

Общее решение неоднородного дифференциального уравнения:

sin 2x

C cos x

sin x;

Рассмотрим примеры применения описанных методов.

Пример. Решить уравнение y

3ex .

Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:

k 2 2k 1 0;	k	k	2	1;
	1		2
Общее решение однородного уравнения:	y	C ex		C	xex .
		1		2

Теперь найдем частное решение неоднородного уравнения в виде: y xr e xQ(x)

1; r 2; Q(x) C; y Cx2ex .

Воспользуемся методом неопределенных коэффициентов.

y 2Cxex Cx2ex ;

y 2Cex 2Cxex 2Cxex Cx2ex .

Подставляя в исходное уравнение, получаем:

2Cex 4Cxex Cx2ex 4Cxex 2Cx2ex Cx2ex 3ex .

2C 3; C 32 .

Частное решение имеет вид: y

Общее решение линейного неоднородного уравнения:

C e x

xex

x 2 e x .

Пример. Решить уравнение

x2 1.

Характеристическое уравнение: k 3

k(k 2

0; k

1; k

Общее решение однородного уравнения: y

e x

e x .

Частное решение неоднородного уравнения:

xr e xQ(x) .

0; r 1; Q(x) Ax2 Bx C.

y Ax3 Bx2 Cx

Находим производные и подставляем их в исходное неоднородное уравнение:

y 3Ax2	2Bx C; y 6Ax 2B; y 6A;
6A 3Ax2				2Bx C x2				1;
3A	1;		2B		0;	6A	C	1;
A		1	;	B	0;	C	1;
		3

Получаем общее решение неоднородного дифференциального уравнения:

y C	C	e	x	C	e	x	1	x	3	x.
y C	C	e		C	e			x		x.
1	2			3			3
							3

ОПЕРАЦИИ НАД СОБЫТИЯМИ

Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта.

Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В.

Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого.

Всего в колоде 13 червонных и 13 бубновых карт.

При вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна 5226 , при вытаскивании второй карты - 2551 , третьей - 5024 ,

четвертой - 23 .
49
Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни
червонных равна P(C )	26	25	24	23 .
	52	51	50	49

Тогда P(C) 1 P(C ) 0,945

Пример. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей?

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.2016356.48 Кб17ELSnabStroiPl_Kursovoi(1).pdf
#
12.03.2016690.29 Кб39EN 1990.2002 Basis of structural design.pdf
#
29.03.201563.65 Кб118energetika__33__33__33_-_kopia.docx
#
29.03.2015431.06 Кб9english.docx
#
07.09.2019372.19 Кб2Erica Lawson - Possessing Morgan.docx
#
29.03.20151.92 Mб9examples_of_typical_problems.pdf
#
28.03.2015159.74 Кб25ExceLab1.doc
#
29.03.2015241.66 Кб21ExceLab1.doc
#
28.03.201563.49 Кб17ExceLab2.doc
#
29.03.2015248.83 Кб16ExceLab2.doc
#
29.03.2015492.03 Кб29ExceLab3.doc