Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

examples_of_typical_problems

.pdf

Скачиваний:

Добавлен:

29.03.2015

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Данные формулы не являются эквивалентными.

Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы и .

( p q) r

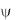( p q) (q p) r

Составим таблицы истинности для заданных формул.

(p q)

q p

q) (q

(p q) (q p) r

Из составленных таблиц видно, что данные формулы не равносильны.

ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ

Пример. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.

	x1
v1	x4	v2

Составим матрицу смежности:

	v1	v2	v3
v1	0	1	0
v2	1	0	1
v3	1	0	0

0	1	0
Т.е. A(D) 1	0	1	- матрица смежности.
1	0	0

Матрица инциндентности:

1 0 1 Т.е. B(D) 1 1 0

	x1	x2	x3	x4
v1	-1	0	1	1
v2	1	-1	0	-1
v3	0	1	-1	0

0 1 1 0

Если граф имеет кратные дуги (ребра), то в матрице смежности принимается aij=k, где k – кратность дуги (ребра).

С помощью матриц смежности и инциндентности всегда можно полностью определеить граф и все его компоненты. Такой метод задания графов очень удобен для обработки данных на ЭВМ.

Пример. Задана симметрическая матрица Q неотрицательных чисел. Нарисовать на

плоскости граф G(V, X), имеющий заданную матицу Q своей матрицей смежности. Найти

матрицу инциндентности R графа G. Нарисованть также орграф G(N, A) , имеющий матрицу смежности Q, определить его матрицу инциндентности С.

		1	1	0	1
	Q	1	2	2	1
	Q	0	2	2	1
		0	2	2	1
		1	1	1	0
			x4
				x3
				v2
	x2				x5
					x6
x1	v1				v3	x7 x8
				x10
	x11				x9

Составим матрицу инциндентности:

	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11
v1	1	1	0	0	0	0	0	0	0	0	1
v2	0	1	1	1	1	1	0	0	0	1	0
v3	0	0	0	0	1	1	1	1	1	0	0
v4	0	0	0	0	0	0	0	0	1	1	1

		1	1	0	0	0	0	0	0	0	0	1
Итого:	R	0	1	1	1	1	1	0	0	0	1	0
Итого:	R	0	0	0	0	1	1	1	1	1	0	0
		0	0	0	0	1	1	1	1	1	0	0
		0	0	0	0	0	0	0	0	1	1	1

Построим теперь ориентированный граф с заданной матрицей смежности.

			x5
			v2
	x2		x7
		х3	x6
x1	v1		х8	v3	x10 x11
			х9
	х17	х15	x14
	x16		х13	x12

Составим матрицу инциндентности для ориетированного графа.

Элемент матрицы равен 1, если точка является концом дуги, -1 – если началом дуги, если дуга является петлей, элемент матрицы запишем как 1.

	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1
C	0	0	0	1	1	1	1	1	1	0	0	0	0	1	1	0	0
C	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1

ПРОИЗВОДНАЯ

Пример. Найти производную функции y

x cos x sin x

cos 2 x .

Сначала преобразуем данную функцию:

sin 2x

cos 2 x

sin 2x

x2 cos 2x

2 cos x( sin x)

sin 2x

x cos 2x

sin x cos x

x cos 2x.

Пример. Найти производную функции y

x2ex2

(2xex2

x 2 2xex2 )( x 2

1) (2x)x 2 e x2

2x3e x2

2x5 e x2

2xex2

2x3e x2

(x 2

1)2

2xex2 (x 4

1 x 2 )

(x 2

1)2

Пример. Найти производную функции y

ln tg

sin x

x cosx

sin x

x cosx

sin x sin x x cosx

x 2

sin2 x

cos

2sin

cos

x cosx

sin2 x

Пример. Найти производную функции y

arctg

2x4

8x3 (1 x8 ) ( 8x7 )2x 4 (1 x8 )2 (8x3 8x11

16x11 ) 8x3 8x11

4x8

(1 x8 )2

(1 x8 )2 (1 x8 )2

(1 x8 )2

x8 )2

8x3 (1

x8 )

8x3

(1 x8 )2

Пример. Найти производную функции y

x 2 e x2

ln x

2xe

2x ln x

2xe

) ln x

xex2 (1 2 ln x 2x 2 ln x)

РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ С ПОМОЩЬЮ ПРАВИЛА ЛОПИТАЛЯ

Пример: Найти предел lim

x 2

ln x

Как видно, при попытке непосредственного вычисления предела получается

неопределенность вида

Функции,

входящие

числитель и знаменатель дроби

удовлетворяют требованиям теоремы Лопиталя.

f (x) = 2x +

;

g (x) = ex;

(x)

lim

;

g (x)

e x

x 1

Пример: Найти предел lim

2arctgx

e x

f (x)

;

g (x) e x

;

x 2

lim

2x 2

1) 1 (

x2 )e x (

Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.

Пример: Найти предел lim

						x
				f	(x)
	1	e	x			1	e	x
f (x)			2					2
	2				2

lim

					x
xe2
x e x .
	x								1
											x) ;				g (x) 1 ex ;
e 2 (1
e 2 (1								2
								2
			x		e		x					1	e	x
			x				2					1		2	(4 x) ;					g (x) ex ;
4							2			4				2	(4 x) ;					g (x) ex ;
4										4
			1	e		x											1
			1			2		(4 x)									1	(4 x)
		4				2		(4 x)							lim	4		(4 x)
		4														4
								e		x									x
										x					x				x
															x
																		e 2

;

f (x)

;

g (x)

lim

2e 2

Следует отметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).

Пример:

Найти предел lim

e x

sin x

f (x)

e x

g (x)

cosx ;

lim

e x

1 2

- опять получилась неопределенность. Применим правило

cos x

Лопиталя еще раз.

(x)

e x ;

g (x)

sin x ;

lim

e x

- применяем правило Лопиталя еще раз.

sin x

(x)

e x ;

(x)

cosx ;

lim

e x

2 ;

cos x

Неопределенности

вида

00 ; 1

;

можно раскрыть с помощью

логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида y f (x) g ( x) , f(x)>0 вблизи точки а при х а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).

Пример: Найти предел lim x x .

x	0
x	0

Здесь y = xx, lny = xlnx.

Тогда

lim ln y

lim x ln x

lim

ln x

правило

lim

1/ x

lim x 0; .

1/ x 2

Лопиталя

Следовательно lim ln y

ln lim

y 0;

lim y

lim x x 1

lim

x 2

Пример: Найти предел

2 x

f (x)

2x;

g (x)

2e2x ;

lim

; - получили неопределенность. Применяем

2 x

правило Лопиталя еще раз.

f (x)

g (x)

4e2x ;

lim

0 ;

2 x

x2e

ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ

Пример. Найти асимптоты и построить график функции y	9x
		.
	9 x 2

Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.

Найдем наклонные асимптоты: k lim		9			0

	9		x	2
x				2

				9
	9x
b lim	9x		lim		x		0
b lim	9 x	2	lim	9			0
x	9 x		x	9

						1

				x2
				x2

y = 0 – горизонтальная асимптота.

- 7. 5

- 5

- 2. 5

2. 5

7. 5

- 2

- 4

- 6

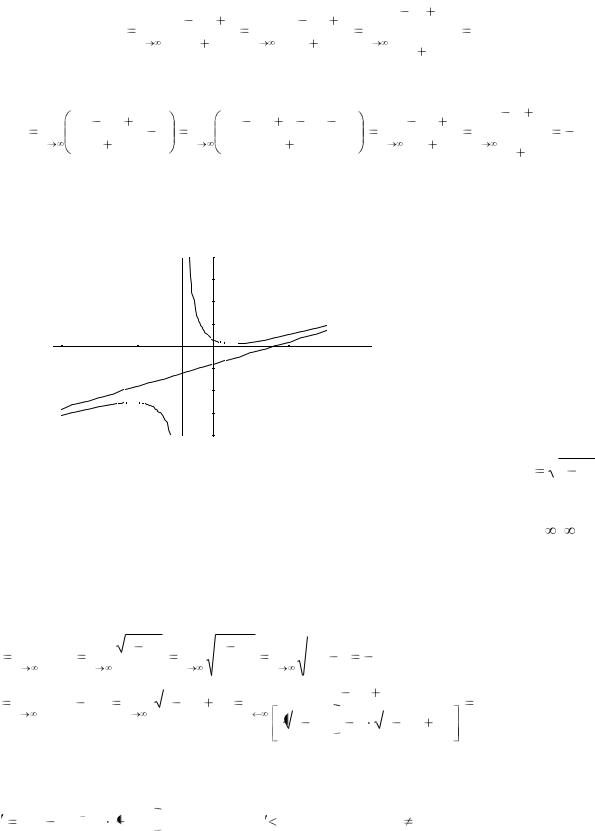
Пример. Найти асимптоты и построить график функции	y	x 2	2x 3	.
		x	2

Прямая х = -2 является вертикальной асимптотой кривой.

Найдем наклонные асимптоты.

2x 3

k lim

lim

x(x 2)

2x 3

2x 3 x2 2x

4x 3

b lim

lim

x 2

Итого, прямая у = х – 4 является наклонной асимптотой.

		20
		15
		10
		5
- 10	- 5	5	10
		- 5
		- 10
		- 15
		- 20

Пример: Методами дифференциального исчисления исследовать функцию y 3 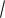1 x3 и построить ее график.

1. Областью определения данной функции являются все действительные числа ( - ; ).

2.Функция является функцией общего вида в смысле четности и нечетности.

3.Точки пересечения с координатными осями: c осью Оу: x = 0; y = 1;

сосью Ох: y = 0; x = 1;

4.Точки разрыва и асимптоты: Вертикальных асимптот нет.

Наклонные асимптоты: общее уравнение y = kx + b;

f (x)

1 x3

lim

lim 3

x3 x3 )

lim ( f (x)

kx)

lim (3 1

x3 x) lim

3 1 x3

x 3 1 x3 x 2

Итого: у = -х – наклонная асимптота.

5. Возрастание и убывание функции, точки экстремума.

y	1	(1 x3 ) 2 / 3	3x 2 . Видно, что у 0 при любом х 0, следовательно, функция
	3

убывает на всей области определения и не имеет экстремумов. В точке х = 0 первая производная функции равна нулю, однако в этой точке убывание не сменяется на возрастание, следовательно, в точке х = 0 функция скорее всего имеет перегиб. Для нахождения точек перегиба, находим вторую производную функции.

y	2x	y = 0 при х =0 и y = при х = 1.


	x3 )5
3 (1

Точки (0,1) и (1,0) являются точками перегиба, т.к. y(1-h) < 0; y(1+h) >0; y(-h) > 0; y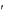(h) < 0 для любого h > 0.

6. Построим график функции.

- 2

- 1

- 2

Пример: Исследовать функцию	y	x3	4	и построить ее график.
		x 2

1.Областью определения функции являются все значения х, кроме х = 0.

2.Функция является функцией общего вида в смысле четности и нечетности.

3. Точки пересечения с координатными осями: c осью Ох: y = 0; x = 3 4

	с осью Оу: x = 0; y – не существует.
4. Точка х = 0 является точкой разрыва lim y	, следовательно, прямая х = 0 является
x 0
вертикальной асимптотой.
Наклонные асимптоты ищем в виде: y = kx + b.

k lim	f (x)	lim	x3	4	lim 1	4		1
	x		x	3		x	3
x		x			x

lim ( f (x)

kx)

lim

Наклонная асимптота у = х.

5. Находим точки экстремума функции.

;

y = 0 при х = 2,

у =

при х = 0.

> 0 при х

(- , 0) – функция возрастает,

y < 0 при х

(0, 2) – функция убывает,

у > 0 при х

(2,

) – функция возрастает.

Таким образом, точка (2, 3) является точкой минимума.

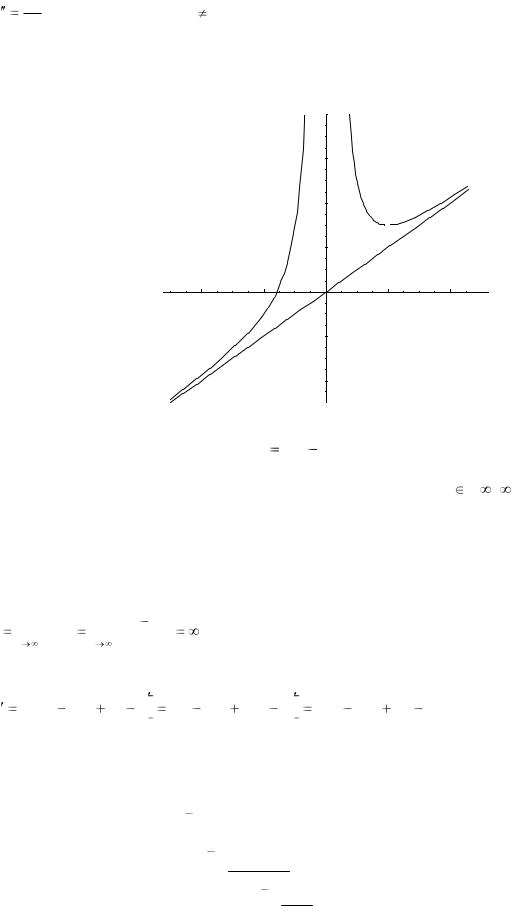
Для определения характера выпуклости/вогнутости функции находим вторую производную.

y	24	> 0 при любом х	0, следовательно,	функция,	вогнутая на всей области
y	x 4	> 0 при любом х	0, следовательно,	функция,	вогнутая на всей области
	x 4
определения.
6. Построим график функции.
			8
			6
			4
			2
		- 4	- 2	2	4
			- 2
			- 4

	Пример: Исследовать функцию y x(x 1)3 и построить ее график.
1.	Областью определения данной функции является промежуток х (- , ).
2.	В смысле четности и нечетности функция является функцией общего вида.
3.	Точки пересечения с осями координат: с осью Оу: x = 0, y = 0;
	с осью Ох: y = 0, x = 0, x = 1.
4.	Асимптоты кривой.

Вертикальных асимптот нет.

Попробуем найти наклонные асимптоты в виде y = kx + b.

k	lim		f (x)	lim	x(x 1)	3	- наклонных асимптот не существует.

			x		x
	x		x	x	x
	x			x
5.	Находим точки экстремума.
y		x(x3 3x 2 3x 1					x 4 3x3 3x 2 x	4x3 9x 2 6x 1

Для нахождения критических точек следует решить уравнение 4х3 – 9х2 +6х –1 = 0. Для этого разложим данный многочлен третьей степени на множители.

Подбором можно определить, что одним из корней этого уравнения является число х = 1. Тогда:

4x3 – 9x2 + 6x – 1			x - 1
4x3 – 9x2 + 6x – 1			x - 1
4x3 – 4x2			4x2 – 5x + 1

	- 5x2	+ 6x
	- 5x2	+ 5x

x - 1 x - 1 0

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.2016356.48 Кб17ELSnabStroiPl_Kursovoi(1).pdf
#
12.03.2016690.29 Кб39EN 1990.2002 Basis of structural design.pdf
#
29.03.201563.65 Кб118energetika__33__33__33_-_kopia.docx
#
29.03.2015431.06 Кб9english.docx
#
07.09.2019372.19 Кб2Erica Lawson - Possessing Morgan.docx
#
29.03.20151.92 Mб9examples_of_typical_problems.pdf
#
28.03.2015159.74 Кб25ExceLab1.doc
#
29.03.2015241.66 Кб21ExceLab1.doc
#
28.03.201563.49 Кб17ExceLab2.doc
#
29.03.2015248.83 Кб16ExceLab2.doc
#
29.03.2015492.03 Кб29ExceLab3.doc

	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11
v1	1	1	0	0	0	0	0	0	0	0	1
v2	0	1	1	1	1	1	0	0	0	1	0
v3	0	0	0	0	1	1	1	1	1	0	0
v4	0	0	0	0	0	0	0	0	1	1	1

	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1
C	0	0	0	1	1	1	1	1	1	0	0	0	0	1	1	0	0
C	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1

	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11
v1	1	1	0	0	0	0	0	0	0	0	1
v2	0	1	1	1	1	1	0	0	0	1	0
v3	0	0	0	0	1	1	1	1	1	0	0
v4	0	0	0	0	0	0	0	0	1	1	1

	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1
C	0	0	0	1	1	1	1	1	1	0	0	0	0	1	1	0	0
C	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1

	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11
v1	1	1	0	0	0	0	0	0	0	0	1
v2	0	1	1	1	1	1	0	0	0	1	0
v3	0	0	0	0	1	1	1	1	1	0	0
v4	0	0	0	0	0	0	0	0	1	1	1

	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1
C	0	0	0	1	1	1	1	1	1	0	0	0	0	1	1	0	0
C	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1