Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

examples_of_typical_problems

.pdf

Скачиваний:

Добавлен:

29.03.2015

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Ф(х1 , х2 ) 2х1 2 28х22

Пример. Привести к каноническому виду уравнение второго порядка: 17x2 + 12xy + 8y2 – 20 = 0.

Коэффициенты а11 = 17, а12 = 6,																			а22 = 8.													А =				17		6
																																				6		8
																																						6			0
Составим характеристическое уравнение:																														17								6			0
																															6					8
																			(17 -									)(8 -					) - 36 = 0
																136 - 8										- 17							+				2 – 36 = 0
																									2 - 25 + 100 = 0
																									1 = 5,								2 = 20.
Итого: 5(х )2				20( у )2				20					0;								x 2								y		2		1			- каноническое уравнение эллипса.
Итого: 5(х )2				20( у )2				20					0;						4									1					1			- каноническое уравнение эллипса.
																			4									1
	Пример. Используя теорию квадратичных форм, привести к каноническому виду
уравнение линии второго порядка. Схематично изобразить график.

																		5x2							2 3xy 3y 2													6 0
	Решение: Составим															характеристическое																							уравнение				квадратичной формы
5x2 2				3y 2 : при a
5x2 2		3xy		3y 2 : при a										5, a										3, a				22			3.
								11								12												22
	a11		a12			5							3						15						3			5								2		3		2		8	12	0
	a12	a22					3	3											15						3			5										3				8	12	0
	a12	a22					3	3
Решив это уравнение, получим																	1 = 2,									2 = 6.
Найдем координаты собственных векторов:
	a11	1 m1		a12 n1			0
											3m1									3n1						0
											3m1									3n1						0						полагая m1 = 1, получим n1 =														3
	a12 m1	a22			1 n1		0
	a12 m1	a22			1 n1		0						3m n 0
																1			1
	a11	2 m2		a12 n2			0
	a11	2 m2		a12 n2			0								m2							3n2						0					полагая m2 = 1, получим n2												=	1
	a12 m2	a22			2 n2			0																									полагая m2 = 1, получим n2												=	3
	a12 m2	a22			2 n2			0							3m		2			3n					2			0																		3
																	2								2
																									(1;		1
Собственные векторы:										(1;						3)																)
									u												u		2
									u												u
								1																				3
																												3

																																								1		2
																	1 3									2;												1		1		2
												u1																						u	2
																																								3
																																										3
																																										3

Находим координаты единичных векторов нового базиса.


e	1	;		3	e		3	;	1
e		;			e			;
1	2		2		2	2		2
	2		2			2		2

Имеем следующее уравнение линии в новой системе координат:

2(x )2 6( y )2 6

Каноническое уравнение линии в новой системе координат будет иметь вид:

(x )2			( y )2	1
	2	12
3

		21

		2
	1.	5
		1
	0.	5
- 2	- 1	1	2
	- 0. 5
	- 1
	- 1.	5
	- 2
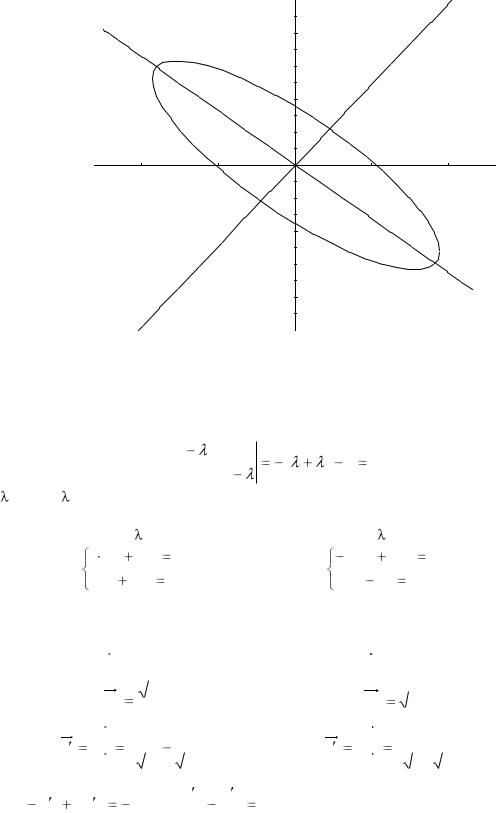
Пример. Используя теорию квадратичных форм, привести к каноническому виду
уравнение линии второго порядка. Схематично изобразить график.


																				5x2								4 6xy 7 y 2											22 0
	Решение: Составим																	характеристическое																					уравнение					квадратичной формы
5x2 4					7 y 2 : при a
5x2 4			6xy		7 y 2 : при a										5, a								2							6, a			22			7.
										11								12															22
	a11			a12			5			2					6						35								7				5					2	24		2	12	11		0
	a12		a22				2	6		7											35								7				5						24			12	11		0
	a12		a22				2	6		7
Решив это уравнение, получим 1 = 1,																														2 = 11.
Найдем координаты собственных векторов:
	a11	1 m1			a12 n1			0
	a11	1 m1			a12 n1			0						2m1									6n1							0				полагая m1 = 1, получим n1											=		2
	a12 m1		a22			1 n1		0																										полагая m1 = 1, получим n1											=		6
	a12 m1		a22			1 n1		0							6m 3n 0																																6
																	1						1
	a11	2 m2			a12 n2			0
	a11	2 m2			a12 n2			0								3m2										6n2							0			полагая m2 = 1, получим n2										=		3
	a12 m2		a22			2 n2		0																												полагая m2 = 1, получим n2										=	6
	a12 m2		a22			2 n2		0								6m					2			2n				2		0																	6
																					2							2

Собственные векторы:											(1;								2			)							(1;					3	)
									u										2						u		2							3
									u																u
										1							3																2
																	3																2

																	1						2								5	;							1	3		5
													u										2								5						u	2		3		5
													u																								u
												1											3							3										2		2
																							3							3										2		2

Находим координаты единичных векторов нового базиса.

		3	;	2			2	;	3
e						e

1	5			5	2		5		5

Имеем следующее уравнение линии в новой системе координат:

(x )2 11( y )2 22

Каноническое уравнение линии в новой системе координат будет иметь вид:

(x )2			( y )2			1
		2			2	1
	22	2		2	2

		4
		2
- 4	- 2	2	4
		- 2
		- 4

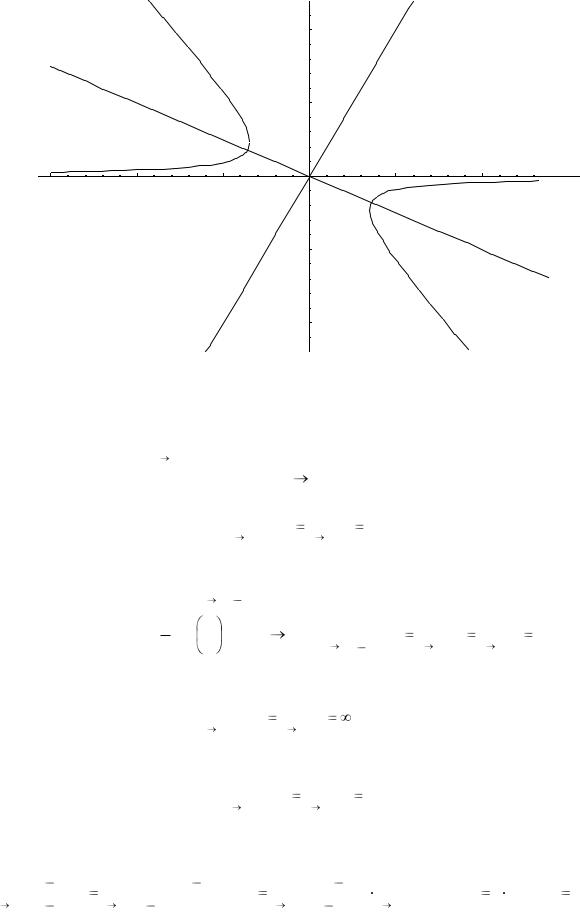
Пример. Используя теорию квадратичных форм, привести к каноническому виду

уравнение линии второго порядка. Схематично изобразить график. 4ху + 3у2 + 16 = 0

Коэффициенты: a11 = 0;					a12 = 2; a22 = 3.
Характеристическое уравнение:										0				2
												2		3
Корни: 1 = -1,	2 = 4.
				Для		1 = -1
		1 m1				2n1			0
		2m1			4n1				0
		m1 = 1;					n1 = -0,5;
			u1 = (1; -0,5)

				u1		5
						5

						2

			u1
	e1		u1		(	2		;	1				)

			u1			5			5
			u1			5			5
											x 2			y 2
Получаем: x 2		4 y 2			16;						x 2			y 2
Получаем: x 2		4 y 2			16;				16					4
									16					4

3	2	4	0

	Для			2 = 4
	4m2			2n2			0
2m2 n2					0
m2 = 1;				n2 = 2;
		u2 = (1; 2)

			u2		5

e2		u2		(	1	;	2	)

		u2			5		5
		u2			5		5

1 -каноническое уравнение гиперболы.

		10
		5
- 15	- 10	- 5	5	10	15
		- 5
		- 10
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ

Пример. Найти предел lim	tg5x
	sin 7x
x 0
Так как tg5x ~ 5x и sin7x ~ 7x при х		0, то, заменив функции эквивалентными
бесконечно малыми, получим:

Пример. Найти предел

Так как 1 – cosx = 2sin2 2x ~ 2

Пример. Найти предел

Пример. Найти предел.

lim

tg5x

lim

sin 7x

x 0

lim

cos x

0, то lim

lim

lim 2x 0 .

при х

x 2

0 1

cos x

x 0

lim

tgx

lim

sin x 2

x 2

x 0

lim	tgmx	lim	mx	m
lim	sin nx	lim	nx	n
x 0	sin nx	x 0	nx	n
Пример. Найти предел.

lim

tgx

tgx0

lim

sin( x x0 )

lim

sin( x

x0 )

lim

(x x0 ) cos x cos x0

cos x cos x0

cos

x x0

Пример. Найти предел.

sin( / 4

sin x

cos x

sin(

/ 4 x)

lim

/ 4

x / 4

/ 4 2 2( / 4 x)

2 2

Пример. Найти предел.

cosx

/ 2

cos(

/ 2 y)

sin y

lim

/ 2

lim

2 y

/ 2

y 0

2 y

Пример. Найти предел.

lim

x 3

lim

4 x

lim

4 z

lim

y x 1

y 4 y 4

lim

lim 1

Пример. Найти предел lim	x2	6x	8	.
	x2	8x	12
x 2

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.

x2 – 6x + 8 = 0;

x2 – 8x + 12 = 0;

D = 36 – 32 = 4;

D = 64 – 48 = 16;

x1 = (6 + 2)/2 = 4;

x1 = (8 + 4)/2 = 6;

x2 = (6 – 2)/2 = 2 ;

x2 = (8 – 4)/2 = 2;

Тогда lim

2)( x

lim

2)( x

x 2

Пример. Найти предел.

lim

домножим числитель и знаменатель дроби на сопряженное

x 0

выражение: lim

lim

0 x(x

1)(

1 x x2 ) x 0 x(x 1)( 1

x x2

1 x x2 )

1 .

Пример. Найти предел.

lim	x2	5x 6	x2 5x 6 (x 2)(x 3) lim	(x	2)(x	3)		3	2		1
		x2 9		(x	3)(x	3)	3		3	6
x 3			x 3

Пример. Найти предел lim	x3	6x 2 11x 6		.
	x	2	3x 2
x 1

Разложим числитель и знаменатель на множители. x2 – 3x + 2 = (x – 1)(x – 2)

x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.

x3 – 6x2 + 11x – 6

x - 1

x3 – x2

x2 – 5x + 6

- 5x2 + 11x

- 5x2 + 5x

6x - 6

x2 – 5x + 6 = (x – 2)(x – 3)

Тогда lim

1)( x

2)( x

(x 1)( x 2)

Пример. Найти предел.

2 sin

2a 2h

cos

2 sin( a h)

sin( a

2h)

2 sin( a

sin a

2 sin( a h)(cosh 1)

lim

h 0

2 lim sin( a

lim

2 sin 2 (h / 2)

2 sin a (

1/ 2)

sin a

4(h / 2)

h 0

lim

2x 2

lim

(x 2

4)( x

lim

x 2

- не определен, т.к. при

3x 4

16x3

24x 2

2)3 (3x

(x 2)(3x

x 2

стремлении х к 2 имеют место различные односторонние пределы -∞ и +∞.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ

Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, членкорреспондент Петербургской АН 1837г)

f (x)	1,	x	рациональн ое число
	0,	x	иррационал ьное число

не является непрерывной в любой точке х0.

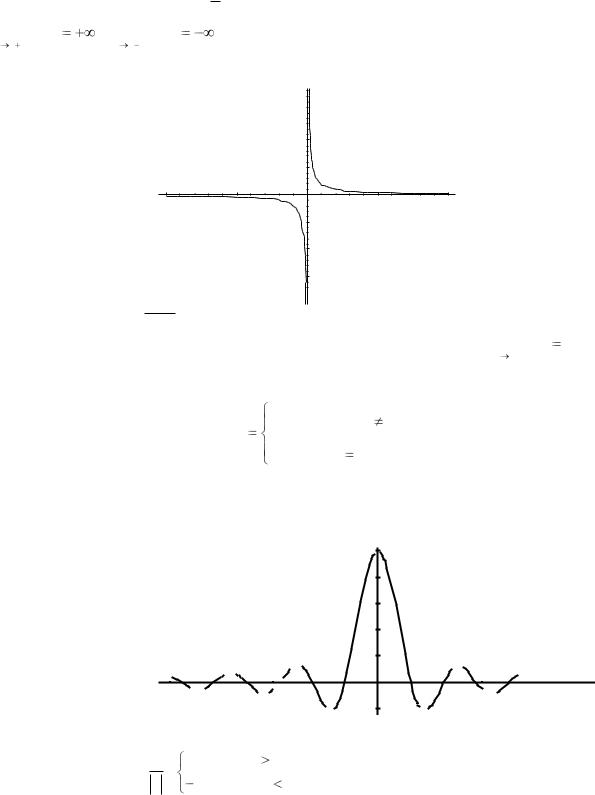
	Пример. Функция f(x) =				1	имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
					х
lim	f (x)	;	lim	f (x)	.
x 0 0			x 0	0
							7.5
							5
							2.5
				-10		-5	5	10
							-2.5
							-5
							-7.5
	Пример. f(x) =			sin x
				x
Функция не определена в точке х = 0, но имеет в ней конечный предел lim									f (x)	1 , т.е. в
								x 0
точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к.
если доопределить функцию:


	sin x		,	при	x 0
f (x)		x

1,		при		x	0

График этой функции:

0. 8

0. 6

0. 4

0. 2

	- 20			- 10	10	20
					- 0. 2
Пример. f(x) =	x	= 1,	при x	0
	x		1, при	x	0

-1

Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какомулибо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.

Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

					x	4,		x	1
				f (x)	x 2	2,			1 x 1
					2x,			x	1
	lim		f (x)	3					lim		f (x)	3
x	1		0						x	1	0
	lim		f (x)	3					lim		f (x)	2
x	1		0						x	1	0
в точке х = -1 функция непрерывна					в точке х = 1 точка разрыва 1 – го рода
					у
							3
							3
							2
							2

	-					0		1				х
				-1
		4		-1

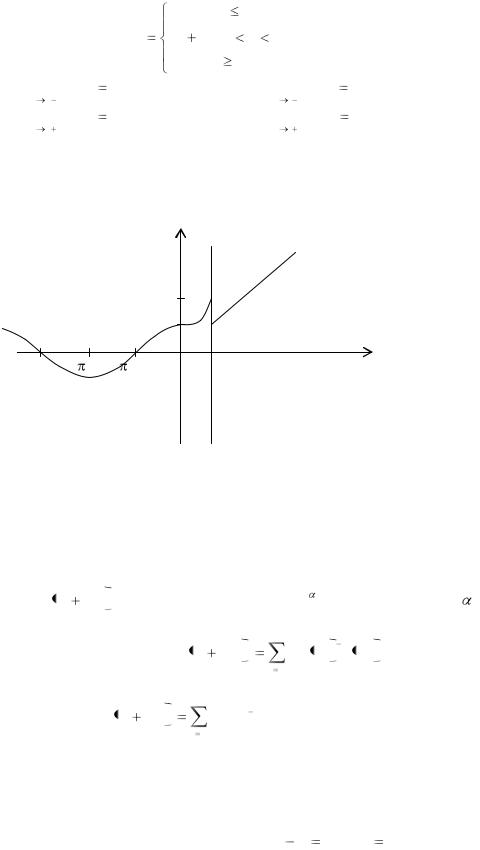
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

			cos x,	x	0
		f (x)	x 2 1,	0	x 1
			x,	x	1
lim	f (x)	1			lim		f (x)	2
x 0	0				x	1	0
lim	f (x)	1			lim		f (x)	1
x 0	0				x	1	0
в точке х = 0 функция непрерывна			в точке х = 1 точка разрыва 1 – го рода

		у
		2
		1
-	- /2	0 1	x

БИНОМ НЬЮТОНА

Пример. В разложении xk y p n найти члены, содержащие х , если k=3, p=2, n=8, =9.

	xk y p n		n		n i	y p i
По фомуле бинома Ньютона имеем:	xk y p n		C i	xk	n i	y p i
			n
			i 0
C учетом числовых значений:
x3 y 2 8	8	x3(8	i) y 2i
x3 y 2 8	C i	x3(8	i) y 2i
	8

Впринципе, можно написать разложение этого выражения в многочлен, определить коэффициеты либо непосредственно, либо из треугольника Паскаля (степень бинома сравнительно невелика), однако, делать это не обязательно, т.к. необходимо найти

только член разложения, содержащий х9.
Найдем число i, соответствующее этому члену: 3(8 i) 9;	i 5.

5	9		10	8!		9		10	8	7	6		9		10		9		10
Находим: С8 x		y			x		y					x		y		56x		y
Находим: С8 x		y		5! 3!	x		y			3	2	x		y		56x		y
				5! 3!						3	2
Пример. В разложении (x							y		z	w)m найти члены, содержащие x . т=9, =6.

По обобщенной формуле бинома Ньютона получаем:

(x y z w)9	9!	xn1	y n2 z n3 wn4

	n1!n2 !n3!n4 !
	n1!n2 !n3!n4 !

Для нахождения полного разложения необходимо определить все возможные значения ni, однако, это связано с громадными вычислениями. Однако, т.к. надо найти только члены, содержащие х6, то n1 = 6, а сумма всех четырех значений п равна 9. Значит, сумма п2 + п3 + п4 = 3.

Рассмотрим возможные значения этих величин:

n2	0	0	3	1	1	0	2	0	2	1
n3	0	3	0	2	0	1	1	2	0	1
n4	3	0	0	0	2	2	0	1	1	1

Искомые члены разложения:
84x6 w3 ;	84x6 y3 ;	84x6 z3 ; 252x6 yz2 ; 252x6 yw2 ;
252x6 zw2 ;	252x6 y2 z;	252x6 z 2 w; 252x6 y2 w; 504x6 yzw;

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы и .

p ( p r)

p ( p r )

Составим таблицы истинности для каждой формулы:

p	r	p	(p r)	p ( p r)

И	И	Л	И	И
И	Л	Л	Л	И
Л	И	И	Л	Л
Л	Л	И	Л	Л

( p

)

p ( p

)

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.2016356.48 Кб17ELSnabStroiPl_Kursovoi(1).pdf
#
12.03.2016690.29 Кб39EN 1990.2002 Basis of structural design.pdf
#
29.03.201563.65 Кб118energetika__33__33__33_-_kopia.docx
#
29.03.2015431.06 Кб9english.docx
#
07.09.2019372.19 Кб2Erica Lawson - Possessing Morgan.docx
#
29.03.20151.92 Mб9examples_of_typical_problems.pdf
#
28.03.2015159.74 Кб25ExceLab1.doc
#
29.03.2015241.66 Кб21ExceLab1.doc
#
28.03.201563.49 Кб17ExceLab2.doc
#
29.03.2015248.83 Кб16ExceLab2.doc
#
29.03.2015492.03 Кб29ExceLab3.doc