Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

examples_of_typical_problems

.pdf

Скачиваний:

Добавлен:

29.03.2015

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости n1 (A, B, C). Вектор AB (1, 3, -5) принадлежит плоскости. Заданная нам

плоскость, перпендикулярная искомой имеет вектор нормали n2 (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то



	i	j	k		3	5		1	5		1	3
	i	j	k

n1 AB n2	1	3	5	i	1	2	j	1	2	k	1	1	11i 7 j 2k .
	1	1	2		1	2		1	2		1	1
	1	1	2		n1 (11, -7, -2). Т.к. точка А принадлежит искомой

Таким образом, вектор нормали

плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11 2 + 7 1 - 2 4 + D = 0; D = -21.

Итого, получаем уравнение плоскости: 11x - 7y – 2z – 21 = 0.

Пример. Найти уравнение плоскости, зная, что точка Р(4, -3, 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

Находим координаты вектора нормали OP = (4, -3, 12). Искомое уравнение плоскости имеет вид: 4x – 3y + 12z + D = 0. Для нахождения коэффициента D подставим в уравнение координаты точки Р:

16 + 9 + 144 + D = 0

D = -169

Итого, получаем искомое уравнение: 4x – 3y + 12z – 169 = 0

Пример. Даны координаты вершин пирамиды А1(1; 0; 3), A2(2; -1; 3), A3(2; 1; 1), A4(1; 2; 5).

Найти длину ребра А1А2.

A1 A2

0;3

{1;

1;0};

A1 A2

1 1 0 2(ед).

2) Найти угол между ребрами А1А2 и А1А4.

A1 A4

1;2

0;5

{0;2;2}

A1 A4

2 2(ед)

A1 A2

A1 A4

(1;

1;0)(0;2;2)

A1 A2

A1 A4

A1 A2

A1 A4

cos

2 2

2 cos

4 cos

cos

A1 A2

A1 A4

;

1200

A1 A2

A1 A4

3) Найти угол между ребром А1А4 и гранью А1А2А3.

Сначала найдем вектор нормали к грани А1А2А3 N как векторное произведение векторов

A1 A3 и A1 A2 .

	A1 A3 = (2-1; 1-0; 1-3) = (1; 1; -2);


			i		j			k

	N		1 1					2				i (0 2) j (0 2) k ( 1 1)																2i 2 j 2k ;						N ( 2; 2; 2)
			1	1				0


	N	2		3
				Найдем угол между вектором нормали и вектором A1 A4 .
				Найдем угол между вектором нормали и вектором A1 A4 .

	N A1 A4						N		A1 A4				cos		2				3		2 2 cos
	N A1 A4					-4 – 4 = -8.
Искомый угол										между вектором и плоскостью будет равен																						= 900 - .
sin				cos						8				2				6		.					arcsin			6
																		6


								4		6				6	3												3
				4)		Найти площадь грани А1А2А3.
																					1						1
																					1						1				3(ед 2 )
																	S						A A		A A				N
																	S						A A		A A				N
																					2		1	2	1	3	2
																					2						2
				5)		Найти объем пирамиды.
														1															1				4	(ед3).
											V					(( A A A A ) A A )														N A A
											V					(( A A A A ) A A )														N A A
														6	1				2			1		3	1	4			6	1		4	3
														6															6				3

6) Найти уравнение плоскости А1А2А3.

Воспользуемся формулой уравнения плоскости, проходящей через три точки.

x 1		y 0 z 3				x 1 y		z 3
2	1	1	0	3	3	1	1	0	(x 1) 2 y( 2) (z 3)(1 1)
2	1	1	0	1	3	1	1	2
	2x	2	2 y	2z	6	0

2x + 2y + 2z – 8 = 0

x + y + z – 4 = 0;

УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИ

Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.

	12		х	5	у	1
уравнение этой прямой в отрезках:		65		65
			х			y
							1

	(65 /12)				(	13)

уравнение этой прямой с угловым коэффициентом: (делим на 5)

							y		12	x		65		12	x	13.
							y		5	x	5		5		x	13.
									5		5		5
нормальное уравнение прямой:
	1		1	12	х	5		у	5		0 ;			cos		= 12/13; sin = -5/13; p = 5.

		13		13		13
122 ( 5)2
122 ( 5)2

Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.

Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.

Уравнение прямой имеет вид:	x	y	1 ,	a = b = 1; ab/2 = 8;	a = 4; -4.
	a	b

a = -4 не подходит по условию задачи.

Итого:	x		y	1 или х + у – 4 = 0.
	4	4

Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.

Уравнение прямой имеет вид:

, где х1 = у1 = 0; x2 = -2; y2 = -3.

x 0

y 0

;

3x 2 y 0.

Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.

k1 = -3; k2 = 2	tg =	2	(	3)	1; = /4.

		1	(	3)2

Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Находим: k1 = 3/5, k2 = -5/3, k1k2 = -1, следовательно, прямые перпендикулярны.

Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

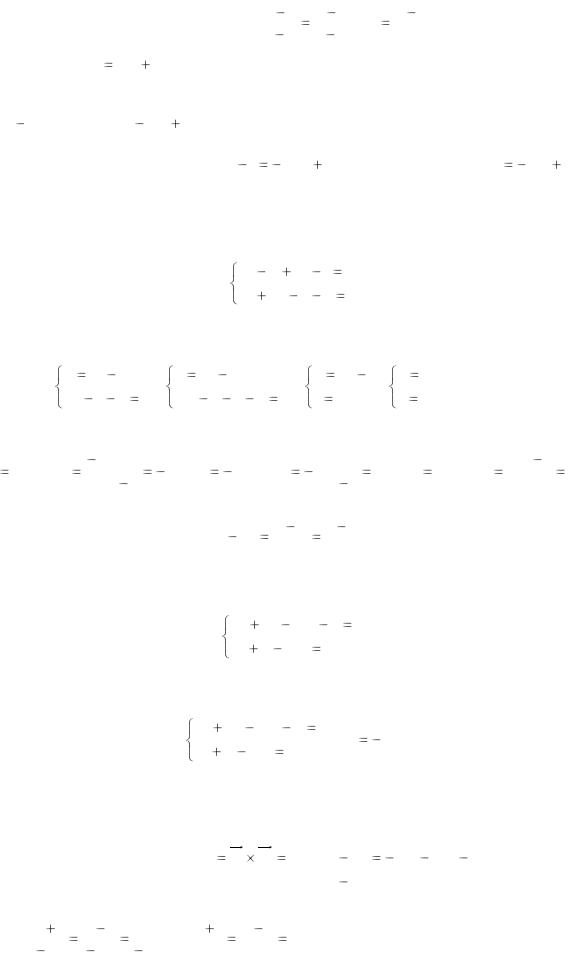
	Находим уравнение стороны АВ:							x	0		y	1	;	x		y 1	; 4x = 6y – 6;
	Находим уравнение стороны АВ:												;				; 4x = 6y – 6;
							6		0		5	1		6	4
2x – 3y + 3 = 0; y			2	x	1.
2x – 3y + 3 = 0; y			3	x	1.
			3
	Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.
k =	3	. Тогда y =			3	x b . Т.к.	высота проходит через точку С, то ее координаты
k =	2	. Тогда y =			2	x b . Т.к.	высота проходит через точку С, то ее координаты
	2				2
удовлетворяют данному уравнению:							1		3	12		b, откуда b = 17. Итого: y						3	x 17 .
удовлетворяют данному уравнению:							1		2	12		b, откуда b = 17. Итого: y						2	x 17 .
									2									2

Ответ: 3x + 2y – 34 = 0.

Пример. Найти каноническое уравнение, если прямая задана в виде: 2x y 3z 1 0

5x 4 y z 7 0

Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.

		y	3z	1	y	3z 1						y		3z 1			y 2	, т.е. А(0, 2, 1).
		4 y z 7 0 12z 4 z 7 0 z 1															z 1
	Находим компоненты направляющего вектора прямой.
m	B1	C1			11;	n		A1		C1		2		3		17;	p		A1	B1	2	1	13.
	B1	C1	1 3					A1		C1		2		3					A1	B1	2	1
	B2	C2	4	1				A2		C2		5		1					A2	B2	5	4
	B2	C2	4	1				A2		C2		5		1					A2	B2	5	4
	Тогда канонические уравнения прямой:
									x		y 2		z	1	.
							11			17		13			.
							11			17		13

Пример. Привести к каноническому виду уравнение прямой, заданное в виде:

16z

3x y 17z 0

Для нахождения произвольной точки прямой, являющейся линией пересечения

указанных выше плоскостей, примем z = 0. Тогда:

2x 3y 16z 7 0; y

3x ;

y 17 z

2x – 9x – 7 = 0;

x = -1; y = 3;

Получаем: A(-1; 3; 0).

Направляющий вектор прямой: S

35i

14 j

7k .

Итого:

x 1

y 3

;

x 1

;

3 cos

КРИВЫЕ ВТОРОГО ПОРЯДКА

Пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в

	x2		y 2
соответствующих вершинах и фокусах эллипса				1 .
соответствующих вершинах и фокусах эллипса	8	5		1 .
	8	5

Для эллипса: c2 = a2 – b2. Для гиперболы: c2 = a2 + b2.

												3

							5

					3

					8						8
Уравнение гиперболы:				x2		y 2	1 .
Уравнение гиперболы:				3	5		1 .
				3	5
Пример.		Составить уравнение гиперболы,						если		ее	эксцентриситет равен 2, а
фокусы совпадают с фокусами эллипса с уравнением									x 2	y 2	1.
фокусы совпадают с фокусами эллипса с уравнением								25		9	1.
								25		9
Находим фокусное расстояние c2 = 25 – 9 = 16.
Для гиперболы: c2 = a2 + b2 = 16,							e = c/a = 2;	c = 2a;			c2 = 4a2; a2 = 4;
b2 = 16 – 4 = 12.
Итого:	x2		y 2	1	- искомое уравнение гиперболы.
Итого:	4	12		1	- искомое уравнение гиперболы.
	4	12

Пример. Уравнение кривой в полярной системе координат имеет вид:

r . Найти уравнение кривой в декартовой прямоугольной системе координат,

определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.

Воспользуемся связью декартовой прямоугольной и полярной системы координат:

				x
r	x2 y 2 ;	cos		x		;



			x2		y 2

		4
x2	y 2	4

		3		x
				x


			x2	y 2
			x2	y 2

3	x 2 y 2 x			4
		15

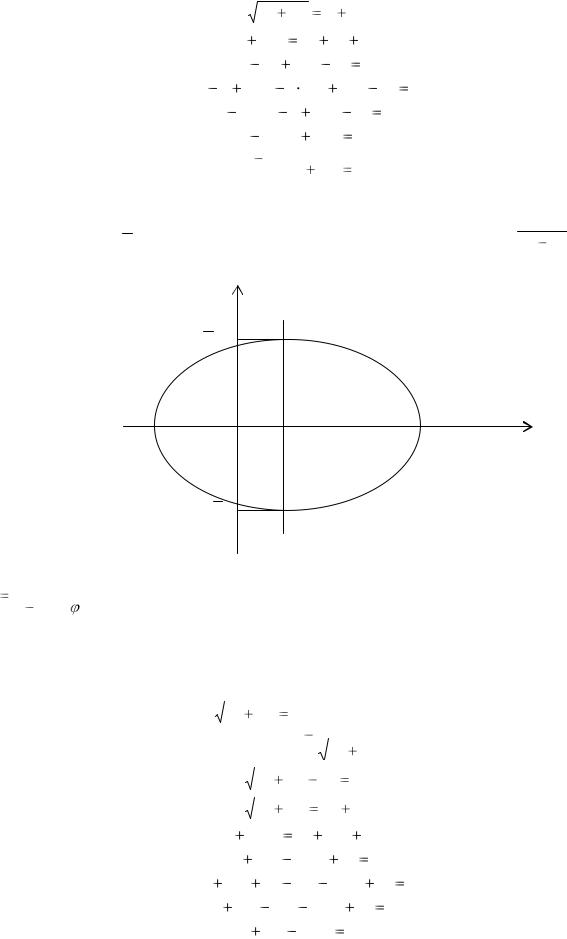
	3	x 2	y 2		x	4
9x2		9y2	16 8x x2
8x2		8x	9y2 16 0
8(x2 x	1/ 4)		8 1/ 4			9y2	16 0
8(x	1/ 2)2		2	9y2		16	0
8(x		1/ 2)2		9y2		18
	(x	1/ 2)2			y 2	1
		9 / 4		2		1
		9 / 4		2

Получили каноническое уравнение эллипса. Из уравнения видно, что центр эллипса сдвинут вдоль оси Ох на 1/2 вправо, большая полуось a равна 3/2, меньшая

полуось b равна 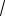2 , половина расстояния между фокусами равно с = 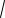a 2 b 2 = 1/2. Эксцентриситет равен е = с/a = 1/3. Фокусы F1(0; 0) и F2(1; 0).

	F1		F2
-1	0	½	1	2	x

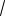- 2

Пример. Уравнение кривой в полярной системе координат имеет вид:

r	9	. Найти уравнение кривой в декартовой прямоугольной системе координат,


4	5 cos

определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.

Подставим в заданное уравнение формулы, связывающие полярную и декартову прямоугольную системы координат.

			9
x2	y 2		9

		4		5x
				5x


				x2	y 2
				x2	y 2

4	x2	y 2	5x		9

4	x2	y 2	5x		9

16x2 16y2			81 90x 25x2
9x2		90x	16y2	81 0
9(x2	10x	25	25) 16y2		81 0
9(x	5)2	225 16y2		81	0
	9(x	5)2	16y2	144

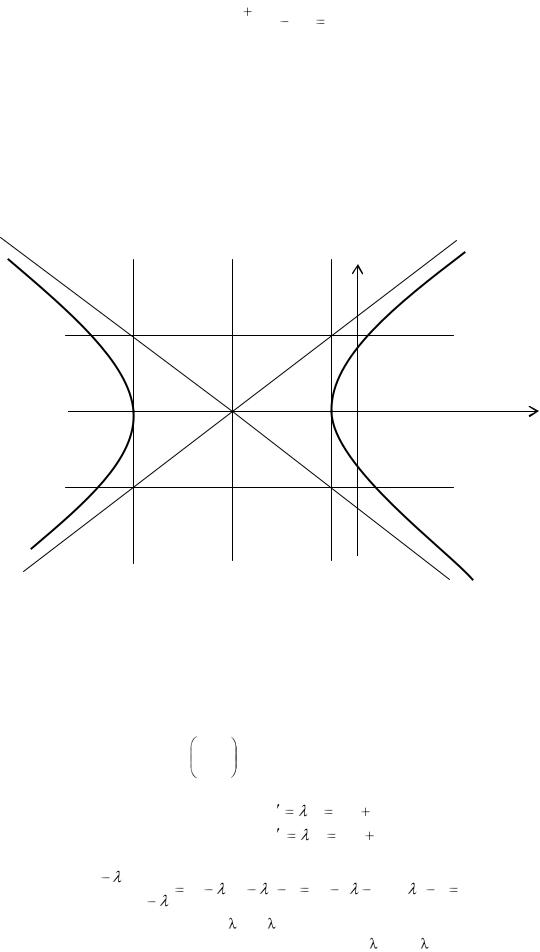
(x 5)2		y 2
			1
16	9		1
16	9

Получили каноническое уравнение гиперболы. Из уравнения видно, что гипербола сдвинута вдоль оси Ох на 5 влево, большая полуось а равна 4, меньшая полуось b равна 3,

откуда получаем c2 = a2 + b2 ; c = 5; e = c/a = 5/4. Фокусы F1(-10; 0), F2(0; 0).

Построим график этой гиперболы.

					0 F2
F1		-9	-5	-1	0 F2	x

-3

СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ

Пример. Найти характеристические числа и собственные векторы линейного

преобразования с матрицей А =	5	4 .
	2	3

Запишем линейное преобразование в виде:					x1	x1	5x1
					x2	x2	2x1
Составим характеристическое уравнение:
		4		(5 )(3	) 8	15	3
	5
	2	3

			2 - 8		+ 7 = 0;

Корни характеристического уравнения:

4x2

3x2

5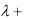 2 8 0

1 = 7; 2 = 1;

Для корня		= 7:	(5 7)x1 4x2		0	2x1	4x2	0
	1		2x1	(3 7)x2	0	2x1	4x2	0

Из системы получается зависимость: x1 – 2x2 = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (t; 0,5t) где t- параметр.

Для корня		= 1:	(5 1)x1 4x2		0	4x1	4x2	0
	2		2x1	(3 1)x2	0	2x1	2x2	0

Из системы получается зависимость: x1 + x2 = 0. Собственные векторы для второго корня характеристического уравнения имеют координаты: (t; -t) где t- параметр.

Полученные собственные векторы можно записать в виде: u1 t(e1 0,5e2 ); u2 t(e1 e2 ).

Пример. Найти характеристические числа и собственные векторы линейного

преобразования с матрицей А =					6	4 .
					4	2
Запишем линейное преобразование в виде:								x1	x1	6x1	4x2
Запишем линейное преобразование в виде:								x2	x2	4x1	2x2
						(6	)x1		4x2	0
						4x1	(2		)x2	0
Составим характеристическое уравнение:
			4	(6		)(2		)	16	12 6	2	2	16 0
	6		4

	4		2
	4		2
						2 - 4		+ 4 = 0;
		Корни характеристического уравнения: 1 =										2 = 2;
Получаем:		(6 2)x1		4x2		0
Получаем:		4x1	4x2	0
		4x1	4x2	0

Из системы получается зависимость: x1 – x2 = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (t; t) где t- параметр.


Собственный вектор можно записать: u (e1	e2 )t .

Пример. Найти характеристические числа и собственные векторы линейного

1 1 3

преобразования А, матрица линейного преобразования А = 1 5 1 .

3 1 1

Составим характеристическое уравнение:

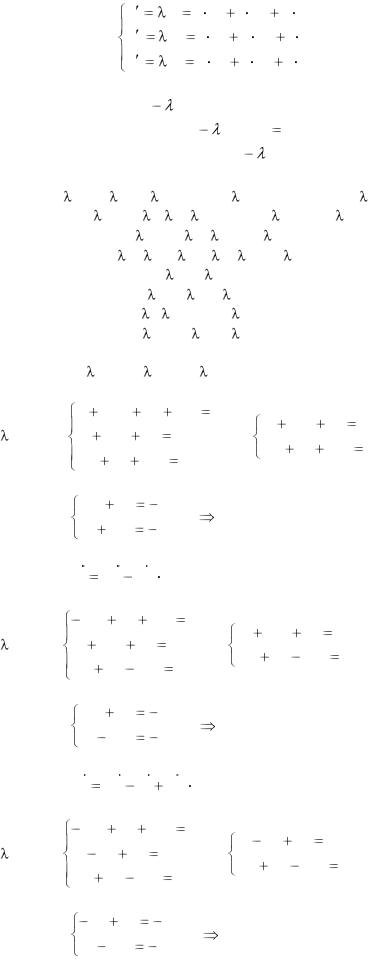
x1	x1	1 x1	1 x2	3 x3
x2	x2	1 x1	5 x2	1 x3
x3	x3	3 x1	1 x2	1 x3

(1 -

)((5 -

)(1 -

) - 1) - (1 -

- 3) + 3(1 - 15 + 3

) = 0

(1 -

)(5 - 5

2 - 1) + 2 +

- 42 + 9 = 0

(1 -

)(4 - 6

2) + 10

- 40 = 0

4 - 6 +

2 - 4 + 6 2 - 3 + 10 - 40 = 0

- 3 + 7

2 – 36 = 0

- 3 + 9 2 - 2 2 – 36 = 0

- 2( + 2) + 9( 2 – 4) = 0

(

+ 2)(-

2 + 9

- 18) = 0

Собственные значения:

1 = -2;

2 = 3;

3 = 6;

2)x1

3x3

7x2

1) Для

1 = -2:

7x2

3x1

3x3

3x1

3x3

Если принять х1 = 1, то

7x2

х2 = 0;

x3 = -1;

3x3

Собственные векторы:

(e1

e3 ) t.

2x1

3x3

2x2

2) Для

2 = 3:

2x2

3x1

2x3

3x1

2x3

Если принять х1 = 1, то

2x2

х2 = -1;

x3 = 1;

2x3

Собственные векторы:

(e1

е3 )

5x1

3x3

3) Для

3 = 6:

3x1

5x3

3x1

5x3

Если принять х1 = 1, то

х2 = 2;

x3 = 1;

5x3

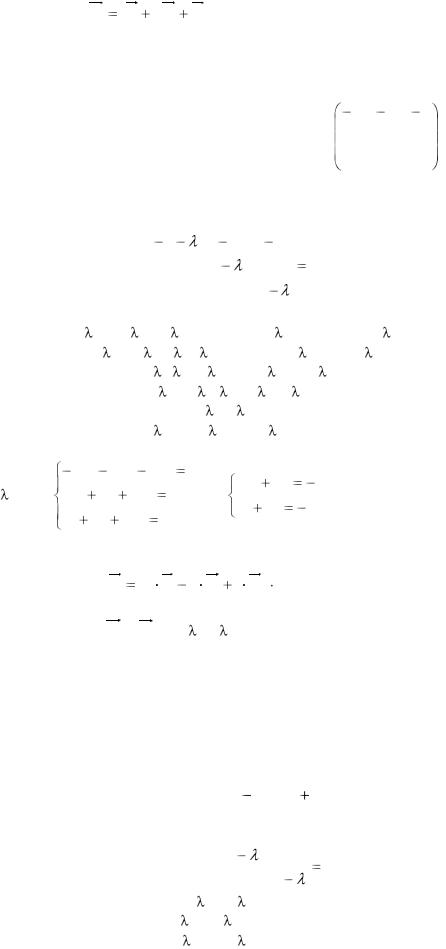
Собственные векторы: u3 (e1 2e2 е3 ) t.

Пример. Найти

характеристические

числа

и собственные

векторы линейного

преобразования А, матрица линейного преобразования А = 2

2 .

Составим характеристическое уравнение:

-(3 +

)((1 -

)(2 -

) – 2) + 2(4 - 2

- 2) - 4(2 - 1 + ) = 0

-(3 +

)(2 -

- 2

2 - 2) + 2(2 - 2 ) - 4(1 +

) = 0

-(3 + )( 2 - 3 ) + 4 - 4 - 4 - 4 = 0

-3 2 + 9 - 3 + 3 2 - 8 = 0

- 3 +

= 0

1 = 0;

2 = 1;

3 = -1;

3x1

2x2

4x3

2x1

2x3

Для 1 = 0: 2x1

2x3

Если принять х3 = 1, получаем

х1 = 0,

х2 = -2

Собственные векторы

1 e3 ) t,

где t – параметр.

Аналогично можно найти u2

и u3

для

2 и 3.

ПРИВЕДЕНИЕ КВАДРАТИЧНЫХ ФОРМ К КАНОНИЧЕСКОМУ ВИДУ

Пример. Привести к каноническому виду квадратичную форму

Ф(х1, х2) = 27 х2		10х х	2	3х2 .
1		1	2	2
Коэффициенты: а11 = 27, а12 = 5, а22 = 3.
		5		0 ;
Составим характеристическое уравнение:	27	5		0 ;
	5	3
(27 - )(3 -		) – 25 = 0
2 - 30 + 56 = 0
1 = 2;		2 = 28;
20

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.2016356.48 Кб17ELSnabStroiPl_Kursovoi(1).pdf
#
12.03.2016690.29 Кб39EN 1990.2002 Basis of structural design.pdf
#
29.03.201563.65 Кб118energetika__33__33__33_-_kopia.docx
#
29.03.2015431.06 Кб9english.docx
#
07.09.2019372.19 Кб2Erica Lawson - Possessing Morgan.docx
#
29.03.20151.92 Mб9examples_of_typical_problems.pdf
#
28.03.2015159.74 Кб25ExceLab1.doc
#
29.03.2015241.66 Кб21ExceLab1.doc
#
28.03.201563.49 Кб17ExceLab2.doc
#
29.03.2015248.83 Кб16ExceLab2.doc
#
29.03.2015492.03 Кб29ExceLab3.doc