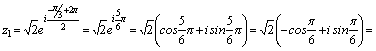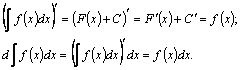|
Комплексным
числом z называется
число вида  ,
где ,
где 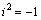 ,
а x и y–вещественные
числа. Число x называется
действительной частью, y–мнимой
частью комплексного числа z.
Это записывают следующим образом: ,
а x и y–вещественные
числа. Число x называется
действительной частью, y–мнимой
частью комплексного числа z.
Это записывают следующим образом: 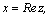 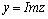 . .
Если x=0,
то число z называют
чисто мнимым; если 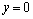 ,
то получается вещественное число ,
то получается вещественное число 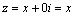 .
Два комплексных числа .
Два комплексных числа 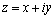 и и 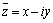 называются
сопряженными. называются
сопряженными.
Два
комплексных числа 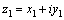 и и 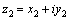 равны
друг другу, если равны
друг другу, если 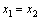 и и 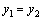 ;
комплексное число z считается
равным нулю, если ;
комплексное число z считается
равным нулю, если 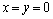 . .
В сякое
комплексное число можно изобразить
на плоскости, т.к. каждому z соответствует
упорядоченная пара вещественных
чисел сякое
комплексное число можно изобразить
на плоскости, т.к. каждому z соответствует
упорядоченная пара вещественных
чисел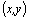 : :
Число z=0
ставится в соответствие началу
координатной плоскости. Такую плоскость
мы в дальнейшем будем называть
комплексной плоскостью, ось
абсцисс–действительной, а ось
ординат–мнимой осью комплексной
плоскости.
Число 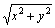 называется
модулем комплексного числа называется
модулем комплексного числа 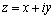 и
обозначается и
обозначается 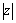 или или  . .
Отметим,
что 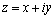 называют
алгебраической формой записи
комплексного числа. называют
алгебраической формой записи
комплексного числа.
|
|
Для
определения положения точки на
плоскости можно пользоваться полярными
координатами 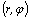 ,
где r–расстояние
точки от начала координат, а φ–угол,
который составляет радиус–вектор
этой точки с положительным направлением
оси Ox.
Положительным направлением изменения
угла φ считается
направление против часовой стрелки.
Воспользовавшись связью декартовых
и полярных координат: ,
где r–расстояние
точки от начала координат, а φ–угол,
который составляет радиус–вектор
этой точки с положительным направлением
оси Ox.
Положительным направлением изменения
угла φ считается
направление против часовой стрелки.
Воспользовавшись связью декартовых
и полярных координат: 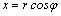 , ,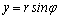 ,
получим тригонометрическую форму
записи комплексного числа ,
получим тригонометрическую форму
записи комплексного числа
|
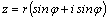
|
(1)
|
где 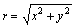 , φ–аргумент
комплексного числа, который находят
из формул , φ–аргумент
комплексного числа, который находят
из формул 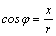 , , 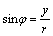 или
в силу того, что или
в силу того, что 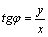 , , 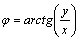 .
Заметим, что при выборе значений φ из
последнего уравнения необходимо
учитывать знаки x и y. .
Заметим, что при выборе значений φ из
последнего уравнения необходимо
учитывать знаки x и y.
Пример1. Записать
в тригонометрической форме комплексное
число 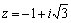 . .
Решение. Найдем
модуль и аргумент комплексного
числа:  .
Угол φ найдем
из соотношений .
Угол φ найдем
из соотношений 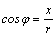 , , 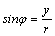 .
Тогда получим .
Тогда получим  .
Очевидно точка .
Очевидно точка 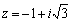 находится
во второй четверти: находится
во второй четверти: 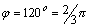 . .
Подставляя
в формулу (1) найденные r и φ,
имеем 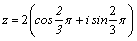 . .
Замечание. Аргумент
комплексного числа определен
неоднозначно, а с точностью до
слагаемого, кратного 2π. Тогда
через 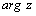 обозначают
значение аргумента, заключенное в
пределах обозначают
значение аргумента, заключенное в
пределах 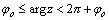 .
Тогда .
Тогда 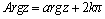 . .
Используя
известную формулу Эйлера 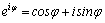 ,
получаем показательную форму записи
комплексного числа. Имеем ,
получаем показательную форму записи
комплексного числа. Имеем
|
|
1.Сумма
двух комплексных чисел  и и 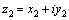 определяется
согласно формуле определяется
согласно формуле 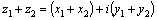 . .
2.Операция
вычитания комплексных чисел определяется
как операция, обратная сложению.
Комплексное число 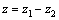 ,
если ,
если 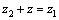 ,
является разностью комплексных
чисел z1 и z2. Тогда ,
является разностью комплексных
чисел z1 и z2. Тогда 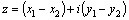 . .
 3.Произведение
двух комплексных чисел 3.Произведение
двух комплексных чисел 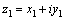 и и 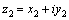 определяется
по формуле определяется
по формуле 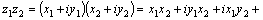  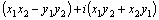 .В
частности .В
частности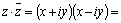 = =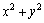 .
Можно получить формулы умножения
комплексных чисел в показательной и
тригонометрической формах. Имеем .
Можно получить формулы умножения
комплексных чисел в показательной и
тригонометрической формах. Имеем 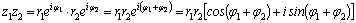 . .
4.Деление
комплексных чисел определяется как
операция, обратная умножению, то есть
число 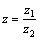 называется
частным от деления z1 на z2,
если называется
частным от деления z1 на z2,
если 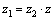 .
Тогда .
Тогда 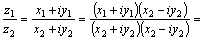
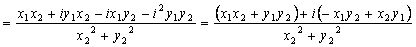 Окончательно Окончательно 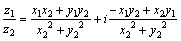 . .
B
показательной и тригонометрической
формах:
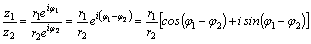 . .
5.Возведение
в целую положительную степень
комплексного числа лучше производить,
если число записано в показательной
или тригонометрической формах.
Действительно,
если  то то 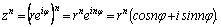
Формула 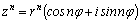 называется
формулой Муавра. называется
формулой Муавра.
6.Извлечение
корня n–й степени из комплексного
числа определяется как операция,
обратная возведению в степень n, 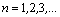 то
есть комплексное число то
есть комплексное число 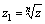 называется
корнем n–й степени из комплексного
числа z, если называется
корнем n–й степени из комплексного
числа z, если 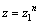 .
Из этого определения следует, что .
Из этого определения следует, что 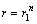 ,
a ,
a 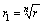 . . 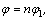 a a 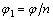 ,
что следует из формулы Муавра, записанной
для числа ,
что следует из формулы Муавра, записанной
для числа  . .
Как
было отмечено выше, аргумент комплексного
числа определен неоднозначно, а с
точностью до слагаемого, кратного 2π.
Поэтому 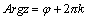 ,
а аргумент числа z1, зависящий от k,
обозначим φk и будем вычислять
по формуле ,
а аргумент числа z1, зависящий от k,
обозначим φk и будем вычислять
по формуле 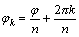 .
Ясно, что существует n комплексных
чисел, n–я степень которых равна
числу z. Эти числа имеют один и тот
же модуль, равный .
Ясно, что существует n комплексных
чисел, n–я степень которых равна
числу z. Эти числа имеют один и тот
же модуль, равный 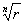 ,
а аргументы этих чисел получаются
при ,
а аргументы этих чисел получаются
при 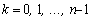 .
Таким образом, в тригонометрической
форме корень n–й степени вычисляют
по формуле: .
Таким образом, в тригонометрической
форме корень n–й степени вычисляют
по формуле:
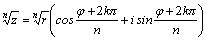 , , 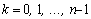 ,
а в показательной–по формуле ,
а в показательной–по формуле 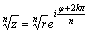 . .
Пример
2. Возвести число  в
пятую степень. в
пятую степень.
Решение. Получим
тригонометрическую форму записи
числа z. 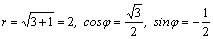 .
Отсюда .
Отсюда 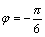 ,
а ,
а 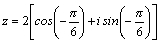 .
Тогда по формуле Муавра получим: .
Тогда по формуле Муавра получим: 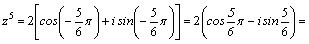
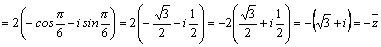 . .
Пример
3. Найти все значения 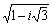 . .
Решение. r=2,
а φ найдем из уравнений 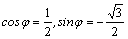 .
Эта точка .
Эта точка 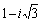 находится
в четвертой четверти, то есть находится
в четвертой четверти, то есть 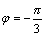 .
Тогда .
Тогда 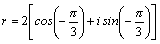 ,
значения корня находим из выражения ,
значения корня находим из выражения 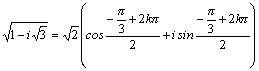 . .
При 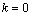 имеем имеем
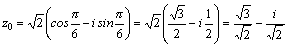 . .
При 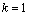 имеем
еще одно значение корня имеем
еще одно значение корня
 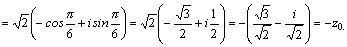
Можно
найти значения корня из числа z,
представив число в показательной
форме. Т.к. r=2, a 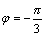 , то , то 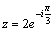 ,
a ,
a 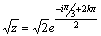 . Тогда
при k=0 имеем . Тогда
при k=0 имеем 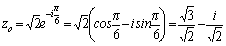 .
Приk=1 имеем .
Приk=1 имеем 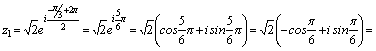 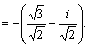
|
|
Функция 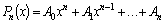 ,
где n–целое число, называется
многочленом или рациональной целой
функцией от x. Число n называют
степенью многочлена. Коэффициенты ,
где n–целое число, называется
многочленом или рациональной целой
функцией от x. Число n называют
степенью многочлена. Коэффициенты 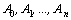 –это
действительные или комплексные числа.
Независимая переменная x также
может быть как действительным, так и
комплексным числом. –это
действительные или комплексные числа.
Независимая переменная x также
может быть как действительным, так и
комплексным числом.
Корнем
многочлена называется такое значение
переменной x, которое обращает
многочлен в нуль.
Теорема
Безу. Число a является корнем
многочлена 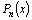 тогда
и только тогда, когда многочлен делится
на x–a без остатка. тогда
и только тогда, когда многочлен делится
на x–a без остатка.
Доказательство. Если
многочлен степени n разделить
на x–a, то очевидно в частном получится
многочлен степени  ,
а в остатке от деления число, то есть ,
а в остатке от деления число, то есть
|
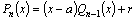
|
(2)
|
Тогда
если x=a–корень многочлена 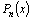 ,
то ,
то 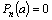 и,
подставляя x=a, в обе части равенства
(2), получим r=0. и,
подставляя x=a, в обе части равенства
(2), получим r=0.
Обратно,
если r=0, то при x=a правая часть
(2) обращается в нуль, тогда и  ,
то есть x=a–корень ,
то есть x=a–корень 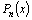 . .
Из
теоремы Безу следует, что если x=a–корень
многочлена, то
|
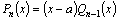
|
(3)
|
Например,
многочлен 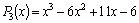 при x=1
обращается в нуль, тогда он делится
на x–1. Разделим многочлен на x–1: при x=1
обращается в нуль, тогда он делится
на x–1. Разделим многочлен на x–1:
Таким
образом, 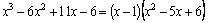 . .
Теорема (доказывается
в курсе алгебры). Всякий
многочлен 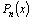 степени степени 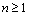 имеет
по крайней мере один корень. имеет
по крайней мере один корень.
Теорема. Всякий
многочлен степени n разлагается
на n линейных множителей вида 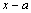 и
множитель, равный коэффициенту при и
множитель, равный коэффициенту при 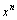 . .
Доказательство. Пусть  .
Он имеет по крайней мере один корень.
Пусть это будет a1. Тогда на основании
теоремы Безу .
Он имеет по крайней мере один корень.
Пусть это будет a1. Тогда на основании
теоремы Безу  ,
где ,
где 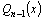 –многочлен
степени –многочлен
степени 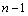 .
Он тоже имеет по крайней мере один
корень. Обозначим его .
Он тоже имеет по крайней мере один
корень. Обозначим его 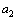 .
Тогда .
Тогда  ,
где ,
где 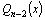 –многочлен
степени –многочлен
степени 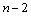 .
Продолжая этот процесс выделения
линейных множителей, дойдем до
соотношения .
Продолжая этот процесс выделения
линейных множителей, дойдем до
соотношения  ,
где ,
где  –многочлен
нулевой степени, то есть некоторое
фиксированное число. Это число,
очевидно, равно коэффициенту A0 при –многочлен
нулевой степени, то есть некоторое
фиксированное число. Это число,
очевидно, равно коэффициенту A0 при 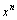 многочлена многочлена 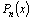 . .
Подставляя
в формулу (3) выражения для 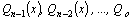 , получим , получим
|
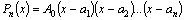
|
(4)
|
Замечание. Числа 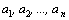 –корни
многочлена –корни
многочлена 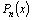 ,
т.к. при подстановке этих чисел в
формулу (4) получаем в правой части
формулы нуль, это и означает, что ,
т.к. при подстановке этих чисел в
формулу (4) получаем в правой части
формулы нуль, это и означает, что  . .
Никакое
значение 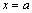 ,
отличное от ,
отличное от 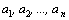 не
может быть корнем многочлена не
может быть корнем многочлена 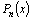 ,
т.к. ни один из множителей в правой
части (4) не обращается в нуль. Отсюда
вытекает, что многочлен n–й степени
не может иметь больше чем n различных
корней. ,
т.к. ни один из множителей в правой
части (4) не обращается в нуль. Отсюда
вытекает, что многочлен n–й степени
не может иметь больше чем n различных
корней.
|
2.
О кратных и комплексных корнях
многочлена
|
|
Если
в разложении многочлена 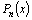 на
множители (4) некоторые линейные
множители окажутся одинаковыми, то
их можно объединить, и тогда разложение
многочлена на множители будет иметь
вид: на
множители (4) некоторые линейные
множители окажутся одинаковыми, то
их можно объединить, и тогда разложение
многочлена на множители будет иметь
вид:
|
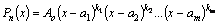
|
(5)
|
При
этом  .
В этом случае корни .
В этом случае корни  называются
корнями кратности называются
корнями кратности 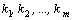 соответственно. соответственно.
Например,
многочлен 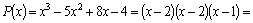 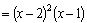 .
Корень .
Корень 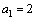 –двукратный
корень этого многочлена, –двукратный
корень этого многочлена, 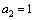 –простой
корень. –простой
корень.
Имеет
место теорема:
всякий многочлен n–ой
степени имеет ровно n корней
(действительных или комплексных).
Теорема (без
доказательства). Если многочлен с
действительными коэффициентами
имеет комплексный корень 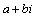 ,
то он имеет и сопряженный корень ,
то он имеет и сопряженный корень  . .
Итак,
в разложении (4) многочлена на множители
комплексные корни входят попарно
сопряженными. Перемножив линейные
множители 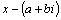 и и 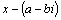 ,
соответствующие паре комплексно
сопряженных корней, получим квадратный
трехчлен с действительными
коэффициентами: ,
соответствующие паре комплексно
сопряженных корней, получим квадратный
трехчлен с действительными
коэффициентами: 
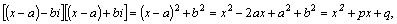
где 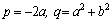 –действительные
числа. –действительные
числа.
Если
корень 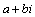 является
корнем кратности k,
то сопряженный корень является
корнем кратности k,
то сопряженный корень 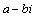 имеет
ту же кратность k.
Это означает, что в разложении
многочлена на множители наряду с
множителями имеет
ту же кратность k.
Это означает, что в разложении
многочлена на множители наряду с
множителями 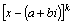 входят
множители входят
множители 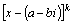 ,
то есть множители ,
то есть множители 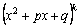 . .
Таким
образом, многочлен с действительными
коэффициентами разлагается на
множители согласно формуле
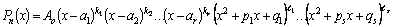 , ,
где
|
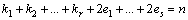
|
(6)
|
|
|
3.
Разложение правильных рациональных
дробей на простейшие
|
|
Рассмотрим
рациональную дробь 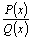 ,
где ,
где 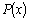 и и 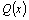 –многочлены
с действительными коэффициентами.
Рациональная дробь называется
правильной, если степень
многочлена –многочлены
с действительными коэффициентами.
Рациональная дробь называется
правильной, если степень
многочлена 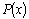 меньше
степени многочлена меньше
степени многочлена 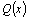 . .
Если
рациональная дробь является
неправильной, то произведя
деление 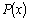 на на 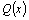 по
правилу деления многочленов, ее
можно представить в виде по
правилу деления многочленов, ее
можно представить в виде 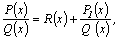 где где 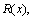 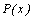 –некоторые
многочлены, а –некоторые
многочлены, а 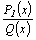 –правильная
рациональная дробь. –правильная
рациональная дробь.
Правильные
рациональные дроби вида
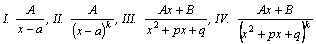 ,
где k–целое
положительное число ≥2, дискриминант
квадратного трехчлена ,
где k–целое
положительное число ≥2, дискриминант
квадратного трехчлена 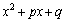 отрицателен,
называются простейшими дробями I,
II, III и IVтипов. отрицателен,
называются простейшими дробями I,
II, III и IVтипов.
Правильную
рациональную дробь, числитель и
знаменатель которой не имеют общих
корней, то есть дробь несократимую
можно разложить на сумму простейших
дробей.
Здесь
имеют место три случая.
1.Все
корни многочлена 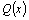 ,
стоящего в знаменателе, действительны
и различны, то есть ,
стоящего в знаменателе, действительны
и различны, то есть 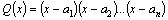 .
Тогда .
Тогда 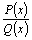 можно
разложить на n простейших
дробей I типа: можно
разложить на n простейших
дробей I типа:
|
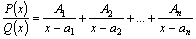
|
(7)
|
2.Все
корни многочлена 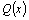 действительны,
но среди них имеются кратные, то
есть действительны,
но среди них имеются кратные, то
есть 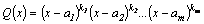 .
Тогда рациональную дробь можно
разложить на сумму простейших
дробей I и IIтипов: .
Тогда рациональную дробь можно
разложить на сумму простейших
дробей I и IIтипов:
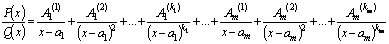 (8) (8)
3.Среди
корней знаменателя правильной
рациональной дроби имеются комплексно
сопряженные не повторяющиеся, то
есть 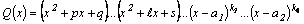 . .
Тогда
дробь 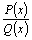 разлагается
на простейшие дроби I, II и III типов.
Запишем ту часть разложения, которая
соответствует множителям разлагается
на простейшие дроби I, II и III типов.
Запишем ту часть разложения, которая
соответствует множителям 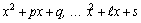 знаменателя: знаменателя:
|

|
(9)
|
Пример
4. Разложить
на простейшие рациональную дробь 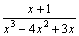 . .
Решение. Разложим
знаменатель дроби на простейшие
множители:
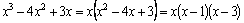 .
Теперь по формуле (7) разложим дробь
на простейшие дроби I типа: .
Теперь по формуле (7) разложим дробь
на простейшие дроби I типа:

Приводя
к общему знаменателю простейшие
дроби и приравнивая числители (то
есть отбрасывая одинаковые
знаменатели), получим
|
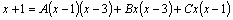
|
(10)
|
Найдем
теперь неизвестные коэффициенты.
Это можно сделать двумя способами.
1–й
способ. Так как многочлены в левой
и правой частях последнего соотношения
тождественно равны, то они равны при
всех значениях x,
входящих в это соотношение, в том
числе и при 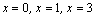 .
Подставляя поочередно эти значения x в
левую и правую части тождества (10),
мы видим, что в правой части (10)
остается отличным от нуля только
одно слагаемое: .
Подставляя поочередно эти значения x в
левую и правую части тождества (10),
мы видим, что в правой части (10)
остается отличным от нуля только
одно слагаемое:
Подставляя
найденные коэффициенты в разложение
дроби, имеем
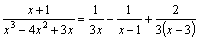
2–й
способ. Произведем преобразование
тождества (10):
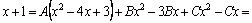
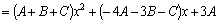 . .
Приравнивая
коэффициенты при 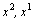 и и 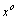 (свободный
член), получим систему уравнений для
определения коэффициентов (свободный
член), получим систему уравнений для
определения коэффициентов 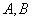 и
C: и
C:
Складывая
теперь первые два уравнения, получим 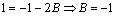 .
И, наконец, .
И, наконец, 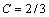 .
Таким образом, получим тот же
результат. .
Таким образом, получим тот же
результат.
Вычисляя
коэффициенты, можно комбинировать
оба способа, это особенно удобно,
если в разложении дроби на простейшие
имеются простейшие дроби всех трех
типов.
Пример
5. Разложить
на простейшие рациональную
дробь 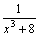 . Решение: . Решение: 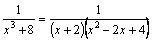 . .
Разложим
дробь: 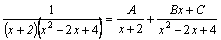 . .
Приводя
простейшие дроби к общему знаменателю
и приравнивая числители, получим:
Систему
уравнений для определения A, B и C можно
получить либо приравнивая коэффициенты
при одинаковых степенях x в
последнем тождестве, либо следующим
образом. Положим в (11) 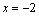 .
Тогда .
Тогда  .
Отсюда .
Отсюда 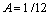 .
Подставляя A в
уравнения, которые получаются из
(12), если приравнять коэффициенты
при .
Подставляя A в
уравнения, которые получаются из
(12), если приравнять коэффициенты
при 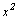 и и 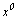 получим: получим:
Так
что имеем окончательно:
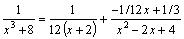 . .
|
|
|
|
Глава
2 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
|
|
|
|
§1.Первообрàзная
функция. Неопределенный интеграл
|
|
Основная
задача дифференциального исчисления
состоит в нахождении дифференциала
данной функции или ее производной.
Многочисленные вопросы науки и
техники приводят к постановке
обратной задачи: для данной
функции 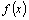 найти
такую функцию найти
такую функцию 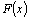 ,
производная которой равнялась бы ,
производная которой равнялась бы 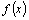 . .
Функция 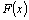 называется первообрàзной для
функции называется первообрàзной для
функции 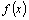 на
данном промежутке, если для всех x из
этого промежутка на
данном промежутке, если для всех x из
этого промежутка 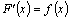 или,
что то же самое, или,
что то же самое, 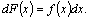
Естественно,
возникает вопрос: для всякой ли
функции существует первообразная?
Ответ на него для достаточно широкого
класса функций дает следующая
теорема.
Любая
непрерывная на отрезке функция имеет
на этом отрезке первообразную.
Очевидно,
первообразная для данной функции
определяется не однозначно. Так, для
функции 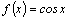 первообразной
является не только первообразной
является не только 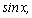 но
и но
и 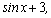 и и 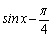 ,
и вообще ,
и вообще 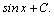
Теорема. Если
функция 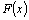 является
первообразной для функции является
первообразной для функции 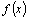 на
отрезке на
отрезке 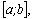 то
всякая другая первообразная
для то
всякая другая первообразная
для 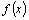 отличается
от отличается
от 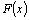 на
постоянное слагаемое, то есть может
быть представлена в виде на
постоянное слагаемое, то есть может
быть представлена в виде 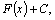 где
C–постоянная. где
C–постоянная.
Доказательство.
По определению первообразной 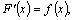 тогда тогда 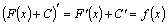 ,
то есть при любом C=const функция ,
то есть при любом C=const функция 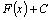 также
является первообразной для также
является первообразной для 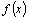 .
Покажем, что первообразных другого
вида нет. Если .
Покажем, что первообразных другого
вида нет. Если 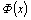 –любая
другая первообразная
функции –любая
другая первообразная
функции 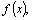 то то 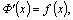 тогда тогда 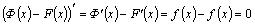 для
любого для
любого 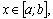 а
это значит, что а
это значит, что 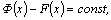 то
есть то
есть 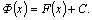
Из
теоремы следует, что
выражение 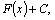 где где 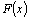 –некоторая
первообразная функции –некоторая
первообразная функции 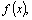 а C–произвольная
постоянная, охватывает
совокупность всех первообразных
функции а C–произвольная
постоянная, охватывает
совокупность всех первообразных
функции 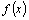 . .
Если 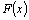 –одна
из первообразных функции –одна
из первообразных функции 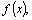 то
выражение то
выражение  где C–произвольная
постоянная, называется неопределенным
интегралом от
функции где C–произвольная
постоянная, называется неопределенным
интегралом от
функции 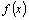 обозначается обозначается 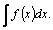
Таким
образом, 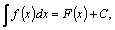
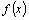 называется подынтегральной
функцией, называется подынтегральной
функцией, 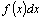 – подынтегральным
выражением, x–переменной
интегрирования,
символ – подынтегральным
выражением, x–переменной
интегрирования,
символ  –знаком
неопределенного интеграла. –знаком
неопределенного интеграла.
Процесс
нахождения неопределенного интеграла
называется интегрированием функции.
Геометрически
неопределенный интеграл 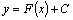 представляет
собой семейство «параллельных»
кривых. представляет
собой семейство «параллельных»
кривых.
|
|


 сякое
комплексное число можно изобразить
на плоскости, т.к. каждому z соответствует
упорядоченная пара вещественных
чисел
сякое
комплексное число можно изобразить
на плоскости, т.к. каждому z соответствует
упорядоченная пара вещественных
чисел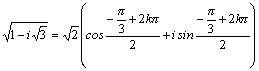 .
.