матем_лекции

 Площадь сектора OAB (рис. 12), ограниченного лучами  и  и кривой , равна                   .

Пример. Найти площадь, ограниченную улиткой Паскаля  (рис.13).

Решение

.

 

 

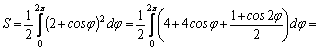
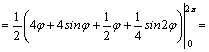
3.Вычисление длины дуги.

Если кривая задана параметрическими уравнениями ,

 

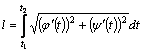, то длина ее дуги , где –значения параметра, соответствующие концам дуги .

Если кривая задана уравнением , то , где a, b–абсциссы начала и конца дуги .

Если кривая задана уравнением , то , где c, d–ординаты начала и конца дуги .

Если кривая задана уравнением в полярных координатах , то , где –значения полярного угла, соответствующие концам дуги .

Пример 1. Вычислить длину дуги кривой  от точки  до .

Решение. , тогда  .

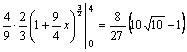Пример 2. Найти длину одной арки циклоиды ,  (рис.11).

Решение. , ,   тогда .

4.Вычисление объема тела вращения.

Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой , отрезком оси абсцисс  и прямыми  (рис.6), вычисляется по формуле .

Объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой , отрезком оси ординат  и прямыми , вычисляется по формуле .

П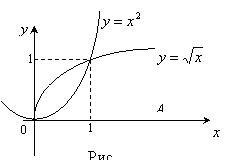ример. Фигура, ограниченная линиями  и , вращается вокруг оси Ox. Найти объем тела вращения (рис. 14).

Решение. Искомый объем можно найти как разность объемов, полученных вращением вокруг оси Ox криволинейных трапеций, ограниченных линиями  и . Тогда 

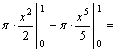
.Глава 4 Функции нескольких переменных§1. Функция двух переменных, ее область определения и графикПусть M–некоторое множество пар действительных чисел , L–некоторое множество действительных чисел.

Функцией двух переменных называется правило, по которому каждой паре чисел соответствует единственное число , при условии, что каждое число  соответствует хотя бы одной паре .

При этом x и y называют независимыми переменными, или аргументами, z–зависимой переменной, или функцией переменных х и у, множество М–областью определения функции, L–множеством значений, или областью изменения функции.

Обозначают: 

Если паре  соответствует число , то пишут , или 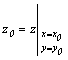. Число  называют при этом частным значением функции при .

Так как каждой паре чисел  соответствует единственная точка  плоскости Оху и обратно, каждой точке  соответствует единственная пара чисел , то функцию двух переменных можно рассматривать как функцию точки и писать  вместо .

В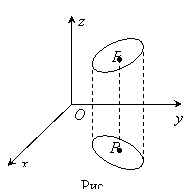 этом случае областью определения функции является некоторое множество точек плоскости Оху.

Если значение  принять за аппликату соответствующей точки  пространства, то множество таких точек образуют, вообще говоря, некоторую поверхность, которую называют графиком функции  (рис.15).

Если функция задана с помощью аналитического выражения, то областью ее определения считают множество всех таких точек плоскости Oxy, для которых это выражение имеет смысл и дает действительные значения функции.

Например, функция z=2x+3y–1 определена на всей плоскости Oxy, графиком ее является плоскость; функция определена при , то есть–внутри круга радиуса r=1 с центром в начале координат, график этой функции–полусфера радиуса R=1.

Определение функции двух переменных легко обобщить на случай большего числа переменных. Так, функцией трех переменных называется правило, по которому каждой тройке действительных чисел  соответствует единственное действительное число , при условии, что каждое число  соответствует хотя бы одной тройке.

Обозначают: , .

Областью определения функции трех переменных является некоторое множество точек в пространстве. Саму функцию трех переменных изобразить с помощью графика в пространстве невозможно.§2. Предел функции двух переменных. Непрерывность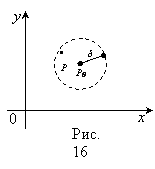δ–окрестностью точки  называется внутренность круга радиуса δ с центром в этой точке.

Иначе говоря, это множество всех точек , для которых выполняется неравенство , то есть расстояние . (рис.16).

Пусть функция z=f(x,y) определена в некоторой области G плоскости Oxy и точка .

Число A называется пределом функции  при стремлении точки к точке , если для любого числа  найдется такая – окрестность точки , что для любой точки P из этой окрестности, кроме, может быть, самой точки, имеет место неравенство .

Обозначают:  или 

Для функции трех переменных – окрестностью точки  является множество всех внутренних точек шара радиуса с центром в точке , определение предела сохраняется.

Функция нескольких переменных называется бесконечно малой, если ее предел равен нулю.

Правила предельного перехода, установленные для функции одной переменной, остаются справедливыми.

Функция  называется непрерывной в точке , если

1) функция определена как в самой точке , так и в некоторой ее окрестности;

2) существует предел ;

3) этот предел равен значению функции в предельной точке: .

Условия (2) и (3) можно заменить равносильным требованием: бесконечно малому расстоянию  соответствует бесконечно малое приращение функции .

Справедлива теорема:

Если функции нескольких переменных и непрерывны в точке , то в той же точке непрерывны и их сумма , разность , произведение  и частное  (последнее–если ).

Точка  называется точкой разрыва функции , если для нее не выполняется хотя бы одно из трех условий в определении непрерывности.

Точки разрыва данной функции могут располагаться как отдельно (изолированные точки разрыва), так и заполнять целые линии (линии разрыва).

Например, функция  имеет единственную точку разрыва , а функция –множество точек разрыва, то есть линию разрыва x+y–1=0.

Областью (открытой областью) называется множество точек плоскости, обладающее свойствами:

каждая точка области принадлежит ей вместе с некоторой окрестностью (свойство открытости);

всякие две точки области можно соединить непрерывной линией, целиком лежащей в этой области (свойство связности).

Точка  называется граничной точкой области G, если любая окрестность этой точки содержит как точки области G, так и точки, ей не принадлежащие.

Множество всех граничных точек области называется ее границей.

Если к открытой области присоединить ее границу, то полученное множество точек называется замкнутой областью.

Область называется ограниченной, если можно подобрать круг, полностью ее покрывающий. В противном случае область называется неограниченной.

Функция  называется непрерывной в области G, если она непрерывна в каждой точке этой области.

Имеет место теорема:

Если функция  непрерывна в ограниченной замкнутой области, то она в этой области

ограничена:;

принимает наименьшее и наибольшее значения (соответственно m и M);

принимает хотя бы в одной точке области любое численное значение, заключенное между m и M.§3. Частные производныеПусть функция определена в области G и точка . Дадим абсциссе приращение , тогда функция z получит приращение , которое называетсячастным приращением по x функции  в точке .

Частной производной по x функции  в точке  называется предел отношения частного приращения по x функции в точке  к приращению  при стремлении  к нулю.

Обозначают частную производную функции z по переменной x , , .

Таким образом, 

Аналогично определяются частное приращение по y функции  в точке :  и частная производная по y функции  в точке :

 (обозначают также , ).

Заметив, что  вычисляется при неизменном y, а – при неизменном x, можно сделать вывод: правила вычисления частных производных совпадают с правилами дифференцирования функций одной переменной, но при вычислении  полагают , а при вычислении  полагают .

Примеры:

1);

;

.

2); ; .

Для функции  одной переменной производная n–го порядка определялась следующим образом: . Аналогично определяются и частные производные высших порядков.

Частной производной n–го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n–1)–го порядка той же функции.

При этом учитывается, что производные можно вычислять по различным переменным. Так, функция двух переменных  имеет две частных производных 1–го порядка:  и , четыре частных производных 2–го порядка:

, , , , восемь частных производных 3–го порядка (от каждой из четырех производных 2–го порядка можно найти производную как по x, так и по y), например, , .

Частные производные высших порядков обозначают также , , , , , . Частная производная 2–го или более высокого порядка, взятая по нескольким различным переменным, называется смешенной частной производной.

Справедлива теорема:

Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.

Так, 

Пример.  Показать, что 

Решение.

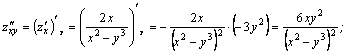
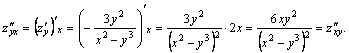§4. Полное приращение и полный дифференциал. Дифференциалы высших порядковПусть дана функция  Предположим, что оба ее аргумента x и y получают соответственно приращения и . Тогда функция  также получает приращение, , которое называется полным приращением функции.

Функция называется дифференцируемой в точке , если ее полное приращение можно представить в виде  где –произвольные приращения аргументов x и y в некоторой окрестности точки , A и B–постоянные (не зависят от ), –бесконечно малая более высокого порядка, чем – расстояние между точками  и .

Главная часть приращения функции , линейная относительно  и , называется полным дифференциалом этой функции (обозначается dz, ).

Таким образом, .

Можно доказать, что если функция дифференцируема в точке , то она имеет в этой точке частные производные  и , причем , .

Следовательно,

	(*)
	(**)

Под дифференциалами независимых переменных условимся понимать их произвольные приращения: , . Тогда .

Аналогично для функции трех переменных 

.

Из формул (*) и (**) следует, что при малых  , то есть , или .

Пример. Вычислить приближенно . Решение. , или ;