матем_лекции

Доказательство. Подставим  в уравнение (9). Получим:  то есть –решение уравнения.

Следствие. Если  и –решения уравнения (9), то  так же является его решением в силу теорем (1) и (2).

Определение. Два решения  и  уравнения (9) называются линейно зависимыми (на отрезке ), если можно подобрать такие числа  и , не равные одновременно нулю, что линейная комбинация этих решений тождественно равна нулю на , то есть если .

Если же таких чисел подобрать нельзя, то решения  и  называются линейно независимыми (на отрезке ).

Очевидно, решения  и  будут линейно зависимы тогда и только тогда, когда их отношение постоянно, то есть  (или наоборот ).

В самом деле, если  и –линейно зависимы, то , где по меньшей мере одна постоянная  или  отлична от нуля. Пусть, например, . Тогда , ,  Обозначая  получим , то есть отношение –постоянно.

Обратно, если  то . Здесь коэффициент при , то есть отличен от нуля, что по определению означает, что  и  являются линейно зависимыми.

Замечание. Из определения линейно независимых решений и рассуждений выше можно сделать вывод, что если  и –линейно независимы, то их отношение не может быть постоянным.

Например, функции  и  при –линейно независимы, так как , так как . А вот функции 5x и x–линейно зависимы, так как их отношение .

Теорема. Если  и –линейно независимые частные решения линейного однородного уравнения второго порядка, то их линейная комбинация , где  и –произвольные постоянные, является общим решением этого уравнения.

Доказательство. В силу теорем 1 и 2 (и следствия к ним)  является решением уравнения (9) при любом выборе постоянных  и .

Если решения  и –линейно независимы, то –общее решение, так как это решение содержит две произвольные постоянные, которые не могут быть сведены к одной.

В тоже время, если бы  и  были линейно зависимыми решениями, то  уже не являлось бы общим решением. В этом случае , где α–константа. Тогда  , где  является постоянной.  не может быть общим решением дифференциального уравнения второго порядка, так как зависит лишь от одной постоянной.

Итак, общее решение уравнения (9):

(11)

где  и –линейно независимые частные решения этого уравнения, а  и –произвольные постоянные.4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиПусть линейное однородное дифференциальное уравнение  (9) имеет постоянные коэффициенты p и q. Будем искать частные решения этого уравнения в виде

где

(12)

Найдем  и  из формулы (12): 

Подставим  в уравнение (9). Получим:   Но . Поэтому

(13)

Квадратное уравнение (13), из которого определяется число k, называется характеристическим уравнением данного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.

Заметим, что для составления характеристического уравнения достаточно в дифференциальном уравнении производные  и  заменить на k и , а функцию y рассматривать как производную нулевого порядка и y заменить на , то есть на единицу.

Например, характеристическое уравнение дифференциального уравнения  имеет вид .

 

 

 

Решим характеристическое уравнение.

(14)

При этих значениях k функции  будут решениями уравнения (9).

Возможны три различных случая.

Случай I. Если , то корни характеристического уравнения действительны и различны, то есть . Тогда частными решениями уравнения (9) будут функции  и . Эти функции линейно независимы и, следовательно, общим решением линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами будет:

(15)

Пример 10. Найти общее решение уравнения .

Решение. Составим характеристическое уравнение и найдем его корни.

 . 

Тогда общее решение дифференциального уравнения составляем по формуле (15): 

Случай II. Если , то в силу формулы (14) характеристическое уравнение (13) имеет равные корни . Такие корни называются кратными. В этом случае одно частное решение дифференциального уравнения будет . Другое частное решение, линейно независимое с , следует выбрать так, чтобы  Тогда , что и означает, что  и –линейно независимы. Найдем , определив функцию , подставляя  в дифференциальное уравнение. . Тогда 

Подставляя  и  в уравнение , получим . Вынося за скобки общий множитель  и сокращая на него, что возможно, так как , получим далее   или  и . Но , поэтому имеем , откуда  и , где a и b–постоянные. Но так как мы ищем какое–либо частное решение дифференциального уравнения, то можно взять  и . Тогда , a  или .

Таким образом, мы имеем два линейно независимых частных решения линейного уравнения:  и . Тогда общее решение этого уравнения будет иметь вид:

или

(16)

Пример 11. Решить дифференциальное уравнение

.

Решение. Составим характеристическое уравнение этого дифференциального уравнения: . Тогда  и . Общее решение данного дифференциального уравнения составляем по формуле (16): .

Случай III. Если , то на основании формулы (14) характеристическое уравнение (13) имеет комплексные корни: 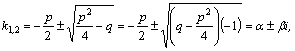 где  . Таким образом,  Тогда частные решения линейного однородного уравнения  будут иметь вид:  

Тогда общее решение уравнения формально можно записать так: , где  и –некоторые комплексные постоянные, подобранные таким образом, чтобы общее решение было действительным. Избавимся в последнем выражении от мнимых величин, воспользовавшись формулами Эйлера:

 

 

Отсюда   где  и –какие угодно (ввиду произвольности постоянных  и`) действительные постоянные. Таким образом, если характеристическое уравнение имеет комплексные корни, то общее решение линейного однородного уравнения находится по формуле:

(17)

Пример 12. Составить общее решение дифференциального уравнения .

Решение. Составим характеристическое уравнение и найдем его корни. Имеем . Отсюда  . Тогда согласно формуле (17) получаем общее решение данного дифференциального уравнения .

В заключение этого пункта составим таблицу, использование которой облегчает студенту отыскание общего решения уравнения

 

.

 

N
1 2 3   4

5. Линейные неоднородные уравнения второго порядка с постоянными коэффициентамиРассмотрим линейное неоднородное уравнение второго порядка

(18)

где p и q–постоянные числа, а –заданная функция. Имеет место теорема о структуре общего решения линейного неоднородного уравнения.

Теорема. Общее решение линейного неоднородного уравнения (18) равно сумме какого–нибудь частного решения этого уравнения  и общего решения  соответствующего однородного уравнения .

Доказательство. Нужно доказать, что сумма  есть общее решение уравнения (18). Подставим эту функцию в уравнение. Имеем  или, учитывая, что производная суммы равна сумме производных, получим

.

Получили тождество, так как выражение, стоящее в первых скобках тождественно равно нулю в силу того, что –решение однородного уравнения, а выражение во вторых скобках равно , так как  является решением неоднородного уравнения. Следовательно,

(19)

является решением линейного неоднородного уравнения. И при этом оно будет общим решением, так как в его состав в силу того, что , входят две произвольные постоянные.

Таким образом, если известно общее решение  однородного уравнения, то основная задача при интегрировании неоднородного уравнения (18) сводится к нахождению какого–либо его частного решения 

Рассмотрим метод неопределенных коэффициентов, с помощью которого в некоторых случаях можно определить решение  неоднородного уравнения.

Случай I. Правая часть уравнения (18) есть показательная функция

.

Ищем частное решение уравнения также в форме показательной функции

,

(20)

где A–неопределенный коэффициент. Отсюда , . Подставим в уравнение

(21)

выражения для  и его производных, получим: . Сократив обе части уравнения на , получим .

Здесь возможны два случая:

1)m не является корнем характеристического уравнения, то есть . Тогда можно найти неизвестный коэффициент A. Получим . И тогда .

2)Число m является корнем характеристического уравнения, то есть . Тогда A найти нельзя и частное решение уравнения (21) нельзя представить в виде .

В этом случае а) если один корень характеристического уравнения равен m, а другой отличен от m, то частное решение уравнения (21) следует искать в виде  и б) если оба корня характеристического уравнения равны m, то частное решение ищут в виде .

Проверим, например, что  в том случае, если m –однократный корень характеристического уравнения, то есть . Подставим в уравнение (21)  и его первую и вторую производные. Если , то   и тогда имеем

Так как , то , а  (см. формулу 14). Значит, неизвестный коэффициент  и , где A уже известно. Но если оба корня характеристического корня равны m, то есть , что и означает, что , то  невозможно найти в виде , а, как было сказано выше, его ищут в виде .

Пример 13. Решить уравнение .

Решение. Найдем общее решение однородного линейного уравнения . Для этого составим характеристическое уравнение . Его корни .