матем_лекции

Это означает, что, подставляя в общее решение значения  и , мы получаем уравнение относительно , из которого может быть найдено значение , если, конечно, в точке  выполнены условия теоремы существования и единственности решения. Тогда функция  и будет искомым частным решением.

Рассмотрим теперь приемы решения некоторых типов дифференциальных уравнений первого порядка.2. Уравнения с разделяющимися переменнымиРассмотрим уравнение вида

(1)

где  и  заданные функции. Решение этого уравнения можно найти, проинтегрировав левую часть уравнения по переменной x, а правую–по y: , где под интегралом понимается одна из первообразных подынтегральной функции.

Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно имеет вид:

,

(2)

где –функции только переменной x, а  и –функции только переменной y.

Легко разделить переменные, если, предположив, что произведение множителей , поделить оба слагаемых уравнения (2) на это произведение. Тогда получим . Интегрируя, запишем

.

Замечание. При делении на  может произойти потеря некоторых решений уравнения (2). Пусть, например, при  . Тогда  является решением уравнения (2). Действительно, так как  и подстановка в уравнение вместо y значения  приводит к тождеству. Аналогично , при котором , так же является решением уравнения.

Пример 1. Решить уравнение .

Решение. Разделим переменные и проинтегрируем: , , где постоянную мы выбрали в виде . Тогда   и . Отметим, что решение дифференциального уравнения, не разрешенное относительно , мы будем называть интегралом этого уравнения. Так что  является общим интегралом данного уравнения.3. Однородные уравненияФункция  называется однородной функцией n–го измерения относительно переменных x и y, если при любом  справедливо тождество:

Пример 2. Функция –однородная третьего измерения, так как .

Пример 3. –однородная нулевого измерения, так как .

Уравнение первого порядка

(3)

называется однородным, если функция  является однородной функцией нулевого измерения относительно x и y.

По условию . Положив в этом тождестве , получим , откуда видно, что однородная функция нулевого измерения зависит только от отношения аргументов. Уравнение (3) в этом случае примет вид

(4)

Сделаем подстановку . Тогда  Подставляя y и  в уравнение (4), получим  а  Разделяя переменные, имеем  Интегрируя, найдем u, а затем подставляя вместо u отношение  получим общее решение (или общий интеграл) уравнения (4).

Замечание. Уравнение вида , где  и –однородные функции одинакового измерения, является однородным, что следует из того, что , а –однородная функция нулевого измерения.

Пример 4. Решить уравнение .

Решение. Разрешим это уравнение относительно . . Разделив числитель и знаменатель дроби на , получим: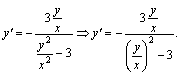 

Далее вводим новую функцию  Так как  то уравнение преобразуется к виду:  Отсюда    Разделяя переменные, получим: , 

Интегрируя, имеем:  Отсюда    Исключая вспомогательную функцию  получаем: , где произвольная постоянная  выбирается так, что .4. Линейные уравнения первого порядкаЛинейным уравнением первого порядка называют уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид

(5)

Здесь  и –заданные непрерывные функции от x или постоянные.

Будем искать решение уравнения (5) в виде произведения двух функций  и  Найдем  и подставим y и  в уравнение (5):  или

(6)

Возьмем функцию  такой, чтобы .

Тогда . Интегрируя, получим частное решение этого уравнения . (Мы нашли именно частное решение уравнения, так как нам достаточно иметь одно какое–нибудь произвольно выбранное отличное от нуля решение уравнения). Подставляя найденную функцию  в уравнение (6), получим уравнение  относительно неизвестной функции  

Пример 5. Решить уравнение .

Решение. Разделим обе части уравнения на :

. Положим  и подставим эти выражения в последнее уравнение:.

Вынесем за скобки общий множитель v и получим

. Тогда  или, сокращая на  обе части последнего уравнения, имеем  и . Интегрируя, получаем . И окончательно 

Пример 6. Конденсатор емкостью c включается в цепь с напряжением E и сопротивлением R. Определить заряд q конденсатора в момент t после включения.

Решение. В момент t заряд конденсатора q и сила тока . К этому же моменту t в цепи действует электродвижущая сила V, равная разности между напряжением цепи E и напряжением конденсатора , то есть .

По закону Ома сила тока , или, иначе, , откуда . Мы получили линейное относительно q уравнение процесса

(7)

Интегрируем это уравнение, полагая  и подставляя q и  в уравнение (7). Имеем  . Тогда  

. Затем получаем  и . Разделим переменные v и t: . Тогда  , где –произвольная постоянная. Далее находим  .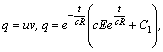

В момент  согласно условию задачи , так как заряд конденсатора отсутствовал. Тогда при  и  имеем  и .

Таким образом, закон рассматриваемого процесса описывается равенством: 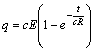.§2. Дифференциальные уравнения второго порядка1. Основные понятияДифференциальное уравнение второго порядка можно записать в виде . Мы будем рассматривать уравнения второго порядка, которые можно разрешить относительно производной второго порядка, то есть записать в виде

.

Для этих уравнений имеет место теорема существования и единственности решения.

Теорема. Если в уравнении  функция  и ее частные производные по аргументам y и  непрерывны в некоторой области, содержащей , то существует и притом единственное решение  уравнения, удовлетворяющее условиям  и .

Эти условия называются начальными условиями. Геометрический смысл этих условий состоит в том, что через заданную точку плоскости  с заданным тангенсом угла наклона касательной  проходит единственная интегральная кривая. Ясно, что если мы будем задавать различные значения , то при постоянных  и  мы получим бесчисленное множество интегральных кривых с различными углами наклона касательных и проходящих через заданную точку.

Общим решением дифференциального уравнения второго порядка называется функция , зависящая от двух произвольных постоянных, которая при любых значениях  и  является решением дифференциального уравнения.

Уравнение , определяющее общее решение, называется общим интегралом дифференциального уравнения.

Если в общее решение подставить конкретные значения  и , то получится частное решение дифференциального уравнения. График частного решения называют интегральной кривой данного дифференциального уравнения.

Рассмотрим методы решения некоторых уравнений второго порядка.

 2. Уравнения, допускающие понижение порядкаа) Рассмотрим простейшее уравнение второго порядка . Общее решение такого уравнения получается путем двукратного интегрирования:

,

где  и –произвольные постоянные, а неопределенные интегралы трактуются как первообразные соответствующих функций.

Пример 7. Решить уравнение .

Решение. Интегрируя первый раз, получаем . Общее решение данного уравнения получаем, интегрируя второй раз: .

б) Рассмотрим уравнение , явно не содержащее искомую функцию y. Положим . Тогда  и уравнение примет вид .

Решаем теперь это уравнение первого порядка относительно p, а затем заменяем p на  и решаем последнее уравнение относительно неизвестной функции y.

Пример 8. Решить уравнение .

Решение. Положим  и подставим  и  в данное уравнение. Получим . Разделим переменные. Тогда . Интегрируя, получим   и . Заменим теперь p на . Имеем  и 

в) Пусть . Это уравнение явно не содержит переменную x. Подстановкой  это уравнение приводят к уравнению первого порядка: .

Далее получившееся уравнение первого порядка решают относительно вспомогательной функции p, а затем, заменяя p на , получают уравнение первого порядка относительно функции y, из которого ее и находят.

Пример 9. Решить уравнение .

Решение. Положим , подставим в уравнение эти выражения производных и получим дифференциальное уравнение первого порядка относительно вспомогательной функции p:

. Отсюда . Это уравнение имеет решение  или , а , а так же решения, удовлетворяющие уравнению .

Разделим переменные в этом уравнении:

Откуда . Полагая , получим дифференциальное уравнение .

Снова разделим переменные: .

Интегрируя, получим: – или . Решение уравнения p=0, то есть y=C, входит в этот общий интеграл при , так как в таком случае  и y является постоянным.

Таким образом, получили общий интеграл дифференциального уравнения , где  и –произвольные постоянные.3. Линейные однородные уравнения второго порядка. Общие свойства решенийДифференциальное уравнение второго порядка называется линейным, если оно имеет вид:

(8)

то есть является линейным относительно неизвестной функции y и ее производных  и . Коэффициенты  и  и правая часть  этого уравнения непрерывны.

Если правая часть уравнения , то уравнение называют линейным неоднородным. Если же , то уравнение имеет вид

(9)

и называется линейным однородным.

Пусть  и –какие–либо частные решения уравнения (9), то есть не содержат произвольных постоянных.

Теорема 1. Если  и –два частных решения линейного однородного уравнения второго порядка, то  так же является решением этого уравнения.

Так как  и –решения уравнения (9), то они обращают это уравнение в тождество, то есть

и

(10)

Подставим  в уравнение (9). Тогда имеем:

 в силу (10). Значит, –решение уравнения.

Теорема 2. Если –решение линейного однородного уравнения второго порядка, а C–постоянная, то  также является решением этого уравнения.