матем_лекции

; ; ;; тогда ; .

;

; ;

; .

Тогда .

Дифференциалы высших порядков определяются так же, как и для функции одной переменной: ,  .

Нетрудно показать, что если x, y –независимые переменные, то ;

.§5. Экстремум функции двух переменныхПусть функция  определена в некоторой области G и точка .

Функция  имеет в точке  максимум, если существует такая окрестность этой точки, что для всех точек  этой окрестности, отличных от , выполняется неравенство .

Аналогично определяется минимум функции.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума). Если –точка экстремума функции , то частные производные  и  в этой точке равны нулю или не существуют.

Точки, в которых частные производные  и  обращаются в нуль или не существуют, называются критическими точками этой функции.

Сформулированный признак не является достаточным: не обязательно критическая точка является точкой экстремума.

Чтобы проверить, есть ли экстремум в критической точке, используют следующую теорему (достаточное условие экстремума).

Пусть в некоторой области, содержащей точку , функция  имеет непрерывные частные производные до 3–го порядка включительно и . Обозначим: . Тогда

1)если , то функция имеет экстремум в точке , причем это максимум, если  и минимум, если ;

2)если , то экстремума в точке  нет;

3)если , требуется дополнительное исследование (экстремум в точке  может быть или не быть).

Пример. Исследовать на экстремум функцию .

Решение. Найдем критические точки функции. ; . Решим систему . Из 2–го уравнения  или . Подставив эти значения в 1–ое уравнение, получим: при , ,  или ; при , , , , . Таким образом, функция имеет четыре критических точки: , , , . Проверим, есть ли экстремум в этих точках.

; ; .

;

в точке O экстремума нет.

 в точке A экстремума нет.

 в точке B экстремум есть, причем , значит, это минимум.  в точке C экстремум есть, причем , значит, это максимум.  –минимум функции, –максимум функции.§6. Наибольшее и наименьшее значения функции двух переменныхПусть функция  непрерывна в замкнутой ограниченной области G, дифференцируема внутри этой области. Чтобы найти наибольшее и наименьшее значения функции в этой области, нужно:

1)найти критические точки, принадлежащие этой области, и вычислить в них значения функции;

2)найти наибольшее и наименьшее значения функции на границе области;

3)из всех найденных значений выбрать наибольшее и наименьшее.

Пример. Найти наибольшее и наименьшее значения функции  в треугольнике, ограниченном прямыми , , .

Решение. 1)найдем критические точки функции.  ;  .

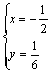Н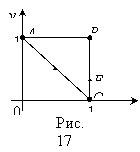айденная критическая точка  не принадлежит области.

2)Исследуем границу области. На участке AB: y=1, . Функция имеет вид то есть ;  при всех функция монотонно возрастает на этом участке, поэтому , .

На участке BC: ,  Функция имеет вид , то есть ,  при –критическая точка на участке BC. ; .

На участке AC: x+y=1, или  . Функция имеет вид , то есть ; ;  при –критическая точка на участке AC. .

3)Выберем наибольшее и наименьшее из найденных значений:      Получим   где , .§7. Скалярное поле. Производная по направлению. ГрадиентПусть в пространстве Oxyz имеется область D, в которой задана функция . В этом случае говорят, что в области D задано скалярное поле, а функцию  называют функцией поля(например, скалярное поле температур, скалярное поле давлений).

Рассмотрим точки области D, в которых функция поля имеет постоянное значение C: . Совокупность этих точек образует некоторую поверхность, которая называется поверхностью уровня, илиэквипотенциальной поверхностью. Уравнение – уравнение поверхности уровня. При различных значениях C получим семейство поверхностей уровня.

Наряду со скалярными полями в пространстве рассматривают также плоские скалярные поля. Функция плоского скалярного поля имеет вид . Плоские скалярные поля изображаются геометрически с помощью линий уровня  (например, изотермы на картах синоптиков).

П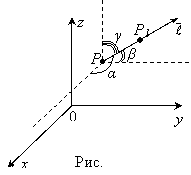усть задана дифференцируемая функция скалярного поля .

Рассмотрим точку  этого поля и луч , выходящий из точки P в направлении единичного вектора  где –углы, образованные вектором  с осями координат (рис.18). Пусть – какая-нибудь другая точка этого луча. Обозначим  – расстояние между точками P и ;  называют величиной перемещения. Приращением функции в направлении  назовем разность .

Производной функции  в точке P по направлению  (обозначают) называется предел отношения приращения функции в направлении  к величине перемещения  при : .

Заметим: если  в точке P, то функция в этом направлении возрастает, если – убывает. Можно сказать, что производная по направлению дает скорость изменения функции в этом направлении.

По условию функция  дифференцируема, значит, ее полное приращение можно представить в виде , где. Разделим обе части на : .

Перейдем к пределу при , учитывая, что , , , , . Получим формулу вычисления производной по направлению: .

Если направление  совпадает с направлением какой–либо из осей координат, то  совпадает с соответствующей частной производной. Пусть, например, луч  направлен по оси Oy. Тогда , то есть ,  и .

Для плоского скалярного поля  .

Градиентом скалярного поля, заданного дифференцируемой функцией , называется вектор, координаты которого совпадают со значениями соответствующих частных производных этой функции:, или .

, где –угол между векторами gradu и . Из этого равенства следует, что  принимает наибольшее значение, когда , то есть , значит, направление  совпадает с направлением gradu.

Таким образом, gradu есть вектор, указывающий направление наибольшего возрастания поля в данной точке и имеющий модуль, равный скорости этого возрастания.

Пример. Найти скорость изменения функции  в точке P в направлении вектора . Найти наибольшую скорость возрастания этой функции в точке P.

Решение. Скорость изменения функции в направлении вектора  дает производная по направлению . Найдем значения частных производных в точке P:;; . Найдем длину вектора : , тогда  и –скорость изменения функции в направлении  (функция возрастает, так как ). Наибольшую скорость возрастания дает модуль градиента.  –наибольшая скорость возрастания функции в точке P.ГЛАВА 5 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ§1. Дифференциальные уравнения первого порядка1. Основные понятияФункциональное уравнение вида , связывающее между собой независимую переменную x, неизвестную функцию y, зависящую от этого x, и ее производные , называется дифференциальным уравнением.

Порядок старшей производной неизвестной функции определяет порядок уравнения. Так, уравнение  является уравнением первого порядка, уравнение –уравнением второго порядка.

Всякая функция , которая, будучи подставлена в дифференциальное уравнение вместе со своими производными, обращает его в тождество, называется решением этого уравнения.

Например, функция  является решением уравнения .

Простейшим дифференциальным уравнением первого порядка является уравнение  или , где y–неизвестная функция от x, а –заданная функция. Для того чтобы определить неизвестную функцию y, нужно проинтегрировать данную функцию . При этом получится множество функций, являющихся решениями дифференциального уравнения.

Решить, или проинтегрировать, дифференциальное уравнение–значит найти все его решения в данной области.

Ясно, что , где –произвольная постоянная, а под интегралом понимается одна из первообразных функций , является общим решением простейшего дифференциального уравнения , где –непрерывная функция.

Выбирая надлежащим образом постоянную , при условии непрерывности функции  можно получить любое решение этого простейшего дифференциального уравнения.

Функция , удовлетворяющая дифференциальному уравнению первого порядка при любом значении произвольной постоянной C, то есть совокупность всех решений этого уравнения, называется его общим решением.

Решения, получаемые из общего при определенных значениях С, называются частными.

Уравнение вида , определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения первого порядка.

Дифференциальное уравнение первого порядка  можно, разрешив относительно производной, представить в виде или .

Общее решение такого уравнения имеет вид  и геометрически представляет собой семейство интегральных кривых, то есть совокупность линий, соответствующих различным значениям постоянной C. Исходя из геометрического смысла производной, интегральные кривые обладают тем свойством, что в каждой их точке  наклон касательной удовлетворяет условию .

Если задать точку , через которую должна проходить интегральная кривая, то тем самым из бесконечного семейства интегральных кривых выделяется некоторая определенная интегральная кривая, которая соответствует частному решению данного дифференциального уравнения.

Аналитически это требование сводится к начальному условию:  при . Задать начальное условие для дифференциального уравнения первого порядка означает указать пару соответствующих друг другу значений независимой переменной  и функции .

Задача отыскания решения дифференциального уравнения , удовлетворяющего начальному условию  при , носит название задачи Коши.

Геометрически задачу Коши можно сформулировать так: найти интегральную кривую дифференциального уравнения , проходящую через заданную точку .

Отметим, что дифференциальные уравнения, как правило, описывают определенный процесс, протекающий в природе. Если условия задачи полностью определяют процесс, то он должен протекать однозначно, то есть решение дифференциального уравнения, которое моделирует этот процесс, должно быть единственным, в то время, как общее решение не дает определенного ответа.

Вопрос о том, в каком случае можно утверждать, что частное решение дифференциального уравнения, удовлетворяющее данному начальному условию, существует, а так же, что оно будет единственным, выясняется теоремой существования.

Теорема существования и единственности решения. Если функция  непрерывна в области, содержащей точку , то уравнение  имеет решение  такое, что .

Если, кроме того, непрерывна и частная производная , то это решение уравнения единственно.

Укажем основное свойство общего решения. Общее решение  дифференциального уравнения  обладает тем свойством, что из него по любому заданному начальному условию  может быть найдено частное решение, удовлетворяющее этому условию.