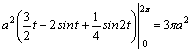матем_лекции
.doc1.Метод разложения, или непосредственное интегрирование–основан на применении свойств 3, 4 неопределенного интеграла.
Пример 1.
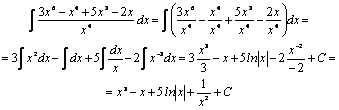
Пример 2.
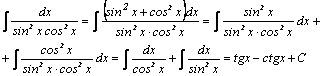
2.Метод замены переменной–основан на использовании формулы
|
|
(1) |
где z–новая
переменная, связанная
с x соотношением ![]() ,
, ![]() непрерывная
монотонная функция, имеющая непрерывную
производную. Справедливость этой формулы
следует из того, что равны дифференциалы
ее левой и правой частей (проверьте).
непрерывная
монотонная функция, имеющая непрерывную
производную. Справедливость этой формулы
следует из того, что равны дифференциалы
ее левой и правой частей (проверьте).
Пример.
![]() =[пусть
=[пусть![]() ,
тогда
,
тогда ![]() ,
, ![]() ]=
]=
=![]() =
=![]() .
.
На основании свойств дифференциала можно записать:
![]() ,
где k, c–константы.
,
где k, c–константы.
Покажем на примерах применение этого соотношения.
Пример 1.
![]()
Пример 2.
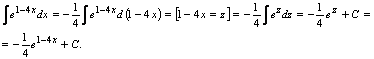
Пример 3.
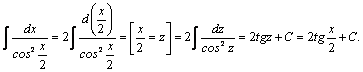
Пример 4.
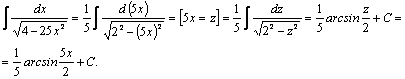
Переобозначив переменные, формулу (1) можно записать в виде
|
|
(2) |
где ![]() новая
переменная.
новая
переменная.
Заметим,
что ![]() .
Это преобразование называется подведением
под знак дифференциала.
В частности,
.
Это преобразование называется подведением
под знак дифференциала.
В частности,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.
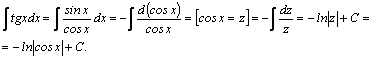
Пример 2.
![]()
Пример 3.
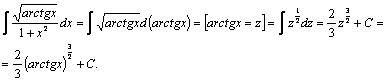
Пример 4.
![]() 3.Метод
интегрирования по частям.
3.Метод
интегрирования по частям.
Если ![]() и
и ![]() –функции,
имеющие непрерывные производные, то
–функции,
имеющие непрерывные производные, то ![]() ,
тогда
,
тогда ![]() ;
проинтегрировав это равенство и учитывая
свойство 2 неопределенного интеграла,
получим формулу
интегрирования по частям:
;
проинтегрировав это равенство и учитывая
свойство 2 неопределенного интеграла,
получим формулу
интегрирования по частям:
![]()
Иногда эту формулу приходится применять последовательно несколько раз.
Отметим три типа интегралов, которые вычисляются методом интегрирования по частям.
![]() где
где ![]() –многочлен,
–многочлен, ![]() В
этих интегралах полагают
В
этих интегралах полагают ![]() .
.
![]()
![]() где
где ![]() –многочлен.
В этих интегралах за u принимают
функцию, являющуюся множителем при
–многочлен.
В этих интегралах за u принимают
функцию, являющуюся множителем при ![]() .
.
![]() где m, n–числа.
Эти интегралы вычисляются двукратным
интегрированием по частям.
где m, n–числа.
Эти интегралы вычисляются двукратным
интегрированием по частям.
Пример 1
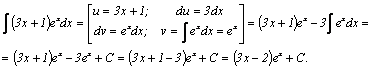
Пример 2.
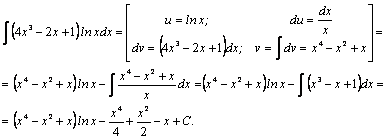
Пример 3.
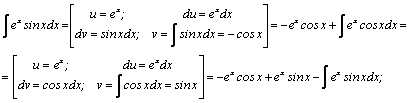
Таким
образом, получили: ![]() перенесем
последнее слагаемое в левую часть:
перенесем
последнее слагаемое в левую часть:
![]()
|
§3. Интегрирование рациональных дробей |
||||||||||||||||||||||||||||||||||
|
Рациональной
дробью называется
выражение вида
Если Если дробь неправильная, из нее можно выделить целую часть, разделив числитель на знаменатель.
Например,
Таким образом, неправильную дробь можно представить в виде суммы целой рациональной функции (многочлена) и правильной дроби:
Простейшими рациональными дробями называются правильные рациональные дроби следующих четырех типов:
где A,
B, C, a,
p, q–числа, Покажем на примерах, как интегрируются дроби каждого типа.
Дробь
1–го типа: Дробь 2–го типа:
Дробь
3–го типа: Дроби 4–го типа интегрируются с помощью специальной рекуррентной формулы, которую мы рассматривать не будем. Если правильная дробь не является простейшей, ее представляют в виде суммы простейших дробей.(См Гл.I, §2, 30)
Пример.
Подынтегральная
функция–правильная рациональная
дробь. Представим ее в виде суммы
простейших дробей, учитывая, что
приведем к общему знаменателю сумму дробей, стоящих в правой части:
приравняем числители дробей:
при
при
приравняем
коэффициенты при
приравняем свободные члены:
Тогда
Вычислим
последний интеграл, введя новую
переменную:
Следовательно, |
||||||||||||||||||||||||||||||||||
|
§4. Интегрирование тригонометрических функций |
||||||||||||||||||||||||||||||||||
|
1.Интегралы
вида
Например,
2.Интегралы
вида Например,
3.Интегралы
вида
Например,
4.Интегралы
Например,
5.Интегралы
вида
Например, Следует заметить, что использование универсальной подстановки нередко приводит к громоздким выкладкам. |
||||||||||||||||||||||||||||||||||
|
§5. Интегрирование простейших иррациональностей |
||||||||||||||||||||||||||||||||||
|
Рассмотрим методы интегрирования простейших видов иррациональностей.
1.
Пример.
2. Пример 1.
Пример 2.
–неправильная рациональная дробь, выделим целую часть:
Получим
3.Интегралы
вида
Пример 1.
Пример 2.
|
||||||||||||||||||||||||||||||||||
|
Страница: 10 из 37; <<назад ^ вперед>> |
||||||||||||||||||||||||||||||||||
|
Глава 3 Определенный интеграл |
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
§1. Задача о площади криволинейной трапеции |
||||||||||||||||||||||||||||||||||
|
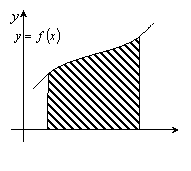
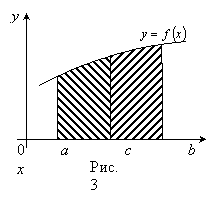
Пусть
П Проведя через точки деления прямые, параллельные оси OY, мы разобьем криволинейную трапецию на n малых криволинейных трапеций. Площадь всей криволинейной трапеции S равна сумме площадей всех малых криволинейных трапеций (рис.2):
Но
вычислить площади малых криволинейных
трапеций не проще, чем площадь большой.
Поэтому поступим следующим образом.
В каждом из отрезков
Очевидно,
чем меньше длины отрезков
|
||||||||||||||||||||||||||||||||||
|
§2. Определение определенного интеграла |
||||||||||||||||||||||||||||||||||
|
К нахождению предела сумм, аналогичных сумме (1), приводит целый ряд задач естествознания. Поэтому вполне естественно изучить этот процесс независимо от конкретного содержания задачи.
Пусть
на отрезке
1.С
помощью точек деления
2.В
каждом из малых отрезков
3.Составим
сумму
Сумма
вида (2) называется интегральной
суммой для функции
4.Наибольшую
из длин малых отрезков обозначим λ
Таким
образом,
Числа a и b называются
соответственно нижним и верхним
пределами интегрирования,
Функция Имеет место теорема существования определенного интеграла.
Всякая
непрерывная на отрезке
Возвращаясь
к §1, отметим факт, выражающий геометрический
смысл определенного интеграла:
определенный интеграл от неотрицательной
непрерывной функции численно равен
площади криволинейной трапеции,
ограниченной кривой Замечания.
1.Определенный
интеграл не зависит от обозначения
переменной интегрирования:
2.Будем
полагать по определению:
3.При
введении понятия определенного
интеграла мы полагали |
||||||||||||||||||||||||||||||||||
|
§3. Свойства определенного интеграла |
||||||||||||||||||||||||||||||||||
|
1
2. где k=const.
3.Если
отрезок интегрирования
Г
4.Если
на отрезке
5.Если
на отрезке
Геометрически
это значит, что криволинейная трапеция,
ограниченная кривой 6.Теорема о среднем значении.
Если
Г
|
||||||||||||||||||||||||||||||||||
|
Страница: 13 из 37; <<назад ^ вперед>> |
||||||||||||||||||||||||||||||||||
|
§4. Производная интеграла с переменным верхним пределом |
||||||||||||||||||||||||||||||||||
|
Если
в определенном интеграле
Обозначим
верхний предел x, а переменную
интегрирования, чтобы не смешивать
ее с верхним пределом, обозначим t.
Таким образом, интеграл с переменным
верхним пределом является функцией
от x:
Имеет
место теорема: производная интеграла
с переменным верхним пределом от
непрерывной функции равна подынтегральной
функции, в которой переменная
интегрирования заменена верхним
пределом: Доказательство. По определению производной
Тогда
Это
значит, что интеграл с переменным
верхним пределом |
||||||||||||||||||||||||||||||||||
|
§5. Формула Ньютона–Лейбница |
||||||||||||||||||||||||||||||||||
|
Теорема.
Если
Доказательство.
Пусть
Это
равенство справедливо для любых При вычислении определенных интегралов будем записывать:
Пример1.
Пример2. |
||||||||||||||||||||||||||||||||||
|
§6. Замена переменной в определенном интеграле |
||||||||||||||||||||||||||||||||||
|
Теорема. Пусть
дан интеграл
1)
2)
3)
при изменении z от α до β значения
Доказательство.
Пусть
Покажем,
что функция
Сравнивая равенства (I) и (II), убеждаемся в справедливости формулы (5). Пример.
при x=0
|
||||||||||||||||||||||||||||||||||
|
§7. Интегрирование по частям в определенном интеграле |
||||||||||||||||||||||||||||||||||
|
Формула
интегрирования по частям в определенном
интеграле выводится так же, как и для
неопределенного интеграла, и имеет
вид Пример.
|
||||||||||||||||||||||||||||||||||
|
§8. Приложения определенного интеграла |
||||||||||||||||||||||||||||||||||
|
Приведем без вывода основные формулы и примеры геометрических приложений определенного интеграла. 1.Вычисление площади в декартовых координатах.
Площадь
криволинейной трапеции, ограниченной
кривой
Площадь
фигуры, ограниченной кривой
Площадь
фигуры, ограниченной двумя непрерывными
кривыми
П
В
случае параметрического задания
кривой
где
Пример1.
Найти площадь, ограниченную линиями
Р Тогда по формуле (8)
Пример
2. Найти площадь фигуры, ограниченной
первой аркой циклоиды
Р
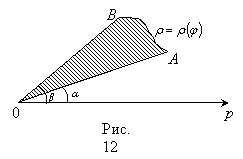
2.Вычисление площади в полярных координатах.
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||

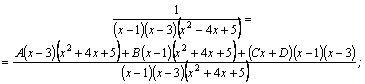
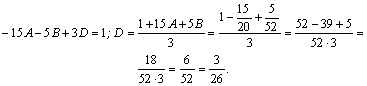
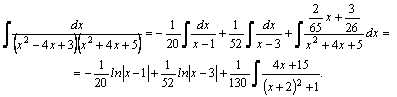
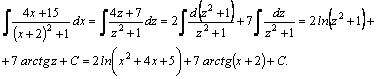
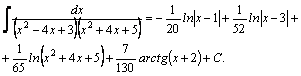
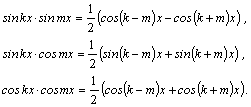
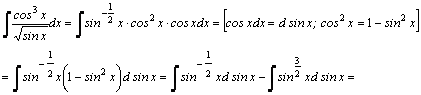
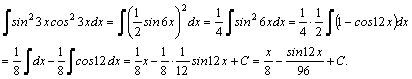
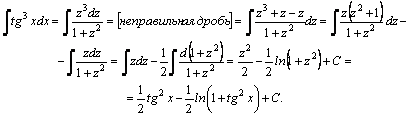
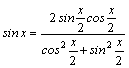 =[после
деления числителя и знаменателя
на
=[после
деления числителя и знаменателя
на 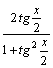 ;
;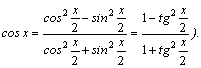
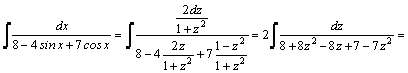
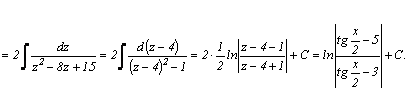
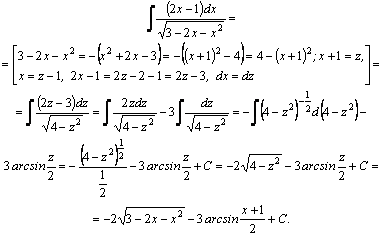
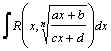 (под
знаком интеграла–рациональная функция
аргументов
(под
знаком интеграла–рациональная функция
аргументов 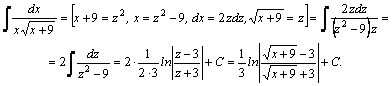
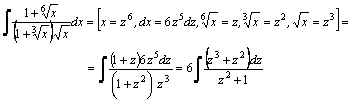
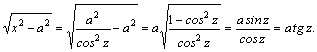
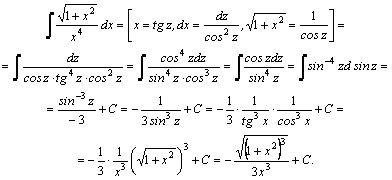
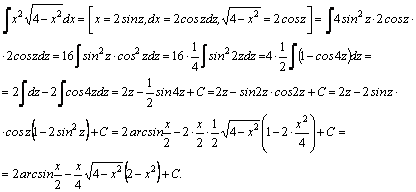
 оставим
перед собой задачу вычислить площадь
криволинейной трапеции. Для этого
разобьем отрезок
оставим
перед собой задачу вычислить площадь
криволинейной трапеции. Для этого
разобьем отрезок 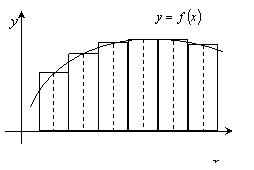 или
или 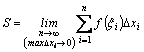
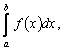 называется интегрируемой на
этом отрезке.
называется интегрируемой на
этом отрезке.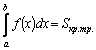
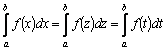 и
т.д.
и
т.д.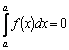
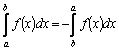
 .
.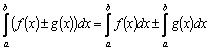
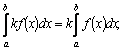
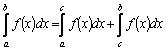 – свойство
аддитивности.
– свойство
аддитивности.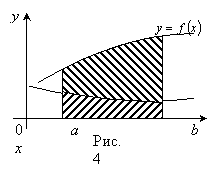 еометрически
это значит, что площадь криволинейной
трапеции с основанием
еометрически
это значит, что площадь криволинейной
трапеции с основанием 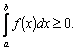
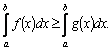
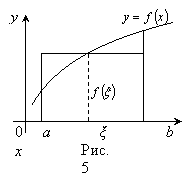 еометрически:
криволинейная трапеция равновелика
прямоугольнику с тем же основанием
еометрически:
криволинейная трапеция равновелика
прямоугольнику с тем же основанием 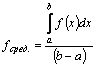 .
.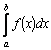 изменять
верхний предел b, то будет меняться
и значение интеграла, то есть интеграл
будет функцией верхнего предела.
изменять
верхний предел b, то будет меняться
и значение интеграла, то есть интеграл
будет функцией верхнего предела.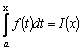 .
.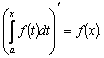
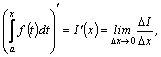 где
где  [первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=
[первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=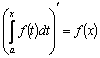
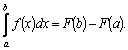
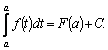 Но
Но  ,
поэтому
,
поэтому 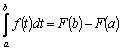 Переобозначив
переменную интегрирования
Переобозначив
переменную интегрирования 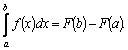
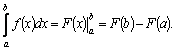
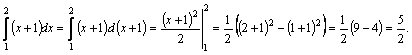
 ,
где
,
где 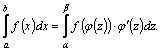
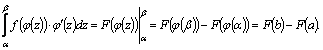
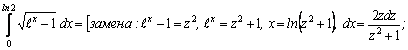
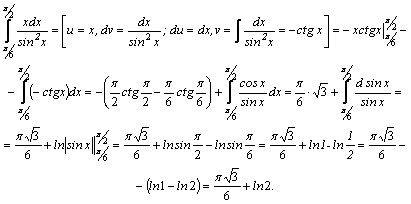
 лощадь
фигуры, ограниченной
кривыми
лощадь
фигуры, ограниченной
кривыми 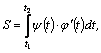
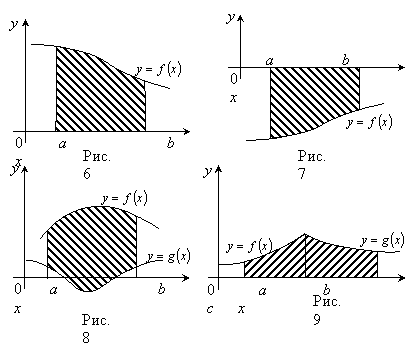
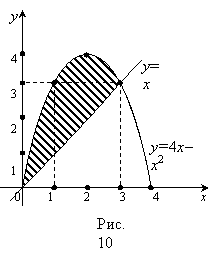 ешение.
Одна из линий–парабола, другая–прямая
(рис.10). Найдем их точки пересечения.
ешение.
Одна из линий–парабола, другая–прямая
(рис.10). Найдем их точки пересечения. 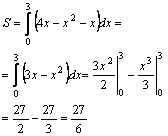
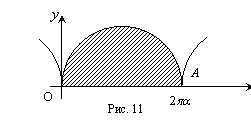 ешение.
Точкам O и A соответствуют
значения параметра
ешение.
Точкам O и A соответствуют
значения параметра