1.3. Законы Ома, Кирхгофа и закон сохранения энергии

Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка. Пусть имеется некоторый участок цепи (рис. 1.7), крайние точки которого обозначены буквами а и b. Пусть ток I течет от точки а к точке b (от более высокого потенциала к более низкому). Следовательно, потенциал точки а(φ_a) выше потенциала точки b(φ_b) на значение, равное произведению тока I на сопротивление R: φ_a=φ_b+IR.

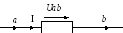
Рис. 1.7

В соответствии с определением напряжение между точками а и b U_ab=φ_a-φ_b.

Следовательно, U_ab=IR, т.е. напряжение на сопротивлении равно произведению тока, протекающего по сопротивлению, на значение этого сопротивления.

В электротехнике разность потенциалов на концах сопротивления принято называть либо напряжением на сопротивлении, либо падением напряжения.

Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.

Рассмотрим вопрос о напряжении на участке цепи, содержащей кроме сопротивления R, ЭДС Е (рис. 1.8, а, б). Найдем разность потенциалов (напряжение) между точками а и с для этих участков. По определению U_aс=φ_a-φ_с. Выразим потенциал точки а через потенциал точки с. При перемещении от точки с к точке b встречно направлению ЭДС Е (см. рис. 1.8, а) потенциал точки b оказывается меньше, чем потенциал точки с, на значение ЭДС Е: φ_b=φ_c-E. При перемещении от точки с к точке b согласно направлению ЭДС Е (рис.1.8, б) потенциал точки b больше, чем потенциал точки с, на значение ЭДС: φ_b=φ_c+E.

Так как ток течет от более высокого потенциала к более низкому, в обеих схемах потенциал точки а выше потенциала точки b на величину падения напряжения на сопротивлении R: φ_а=φ_b+IR.

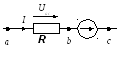
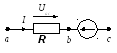
а) б)

Рис. 1.8

Таким образом, для рис. 1.8, а:

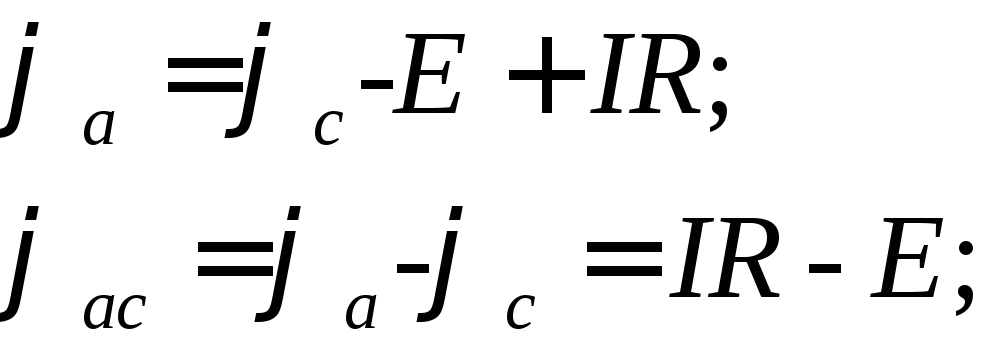(1.1)

для рис. 1.8, б:

(1.2)

Положительное направление напряжения U_aс показывают стрелкой от а к с. Согласно определению, U_са=φ_с-φ_а, поэтому U_ас=-U_са, т.е. изменение чередования индексов равносильно изменению знака этого напряжения. Следовательно, напряжение может быть как положительной величиной, так и отрицательной.

Закон Ома для участка цепи, не содержащего ЭДС Е, устанавливает связь между током и напряжением на этом участке. Применительно к рис.1.7

или . (1.3)

Закон Ома для участка цепи, содержащего источник ЭДС Е, позволяет найти ток этого участка по известной разности потенциалов (φ_a-φ_с) на концах этого участка цепи и имеющейся на участке ЭДС Е.

Так, из уравнения (1.1) для схемы рис.1.8, а следует

.

Из уравнения (1.2) для схемы рис.1.8, б следует:

.

В общем случае

. (1.4)

Все электрические цепи подчиняются первому и второму законам Кирхгофа.

Первый закон Кирхгофа можно сформулировать двояко:

1) алгебраическая сумма токов, подтекающих к какому-либо узлу схемы, равна нулю;

2) сумма подтекающих к любому узлу токов равна сумме утекающих от этого узла токов.

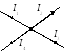
Рис. 1.9

Применительно к рис.1.9, если подтекающие токи к узлу считать положительными, а вытекающие - отрицательными, то согласно первой формулировке I₁-I₂-I₃-I₄=0; согласно второй I₁=I₂+I₃+I₄. Физически первый закон Кирхгофа означает, что движение электрических зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются. В противном случае изменялись бы потенциалы узлов и токи в ветвях.

Второй закон Кирхгофа также можно сформулировать двояко:

1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС, входящих в данный контур:

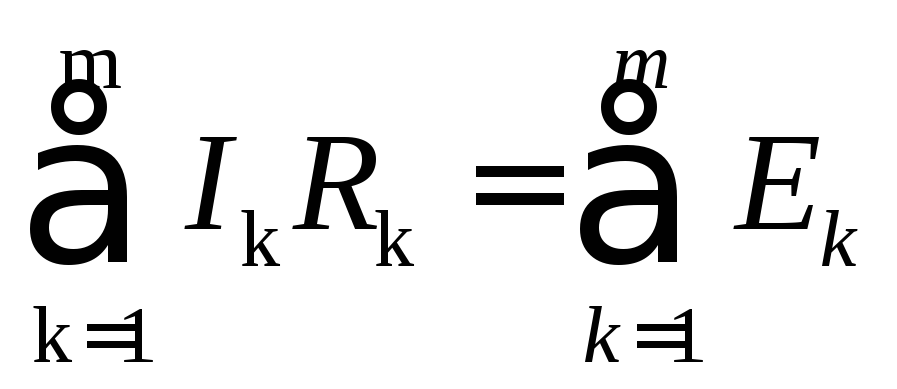, (1.5)

где m - число резистивных элементов; п – число ЭДС в контуре (в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);

2) алгебраическая сумма напряжений вдоль любого замкнутого контура

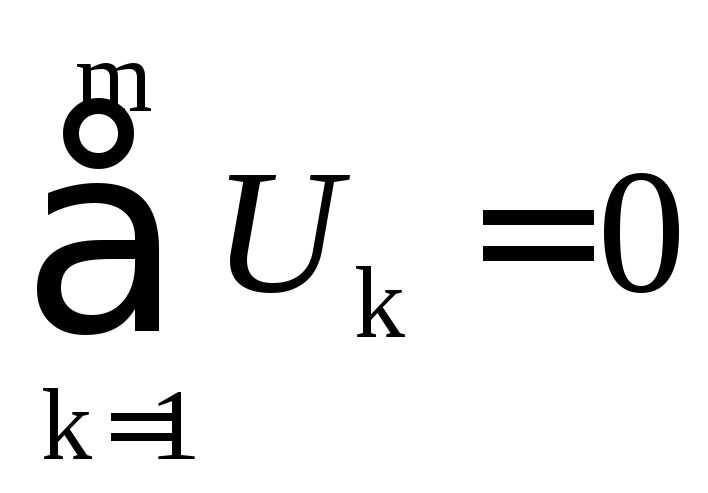, (1.6)

где т - число элементов контура.

Второй закон Кирхгофа является следствием равенства нулю циркуляции вектора напряженности электрического поля вдоль любого замкнутого контура в безвихревом поле.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

При протекании токов по сопротивлениям в них выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой за то же время источником питания. Если направление тока I, протекающего через источник ЭДС E, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени, равную EI, и произведение ЕI входит в уравнение энергетического баланса с положительным знаком. Если же направление тока I встречно ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение ЕI войдет в уравнение энергетического баланса с отрицательным знаком. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид

. (1.7)

В случае питания электрической цепи не только источниками ЭДС, но и источниками тока, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Предположим, что к узлу а схемы подтекает ток J от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна U_аbJ. Общий вид уравнения энергетического баланса:

. (1.8)

1.4. Эквивалентные преобразования пассивных участков

электрической цепи

При наличии в цепи только одного источника энергии в большинстве случаев цепь можно рассматривать как смешанное соединение источника и приемников энергии, т.е. нескольких резисторов, соединенных между собой параллельно, включенных последовательно с другими сопротивлениями (рис.1.10). Расчет смешанного соединения целесообразно начинать с определения эквивалентной проводимости параллельного соединения, а на основании этой проводимости легко найти обратную величину - эквивалентное сопротивление разветвления R. Для схемы, приведенной на рис. 1.10, а:

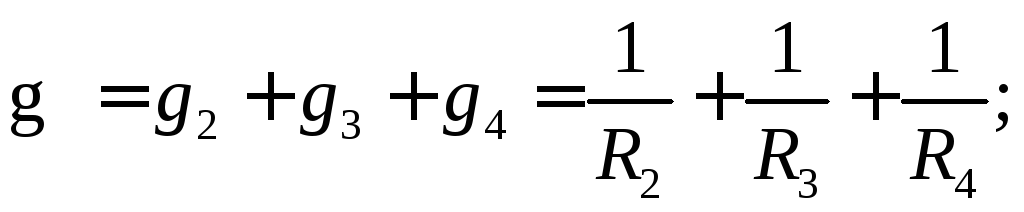
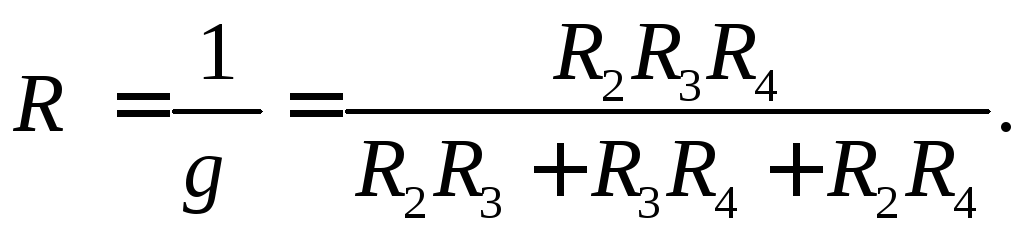
После замены разветвления эквивалентным сопротивлением (рис. 1.10, б) цепь можно рассчитывать как последовательное соединение; ток в неразветвленной части цепи:

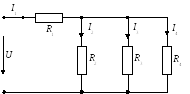
а) б)

Рис. 1.10

В ряде случаев расчет сложной схемы, состоящей из линейных сопротивлений, существенно упрощается, если в этой схеме заменить группу сопротивлений другой эквивалентной группой, в которой сопротивления соединены иначе, чем в замещаемой группе. Взаимная эквивалентность двух групп сопротивлений выразится в том, что после замены электрические условия во всей остальной схеме не изменятся.

Рассмотрим преобразование звезды в треугольник и треугольника в звезду. Соединение трех сопротивлений, имеющих вид трехлучевой звезды, называют звездой (рис. 1.11), а соединение трех сопротивлений так, что они образуют собой стороны треугольника, - треугольником (рис.1.12). Обозначим токи, подтекающие к узлам 1, 2, 3, через I₁, I₂ и I₃. Выведем формулы преобразования. С этой целью выразим токи I₁, I₂ и I₃ в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.

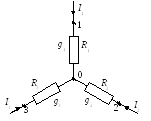
Рис. 1.11

Для звезды:

, (1.9)

; ;, (1.10)

где φ_о,φ₁,φ_2,φ₃ - потенциалы в точках 0, 1, 2, 3 соответственно. Подставим (1.10) в (1.9) и найдем φ₀:

.

Откуда

. (1.11)

Подставим _о в выражение (1.10) для тока I1:

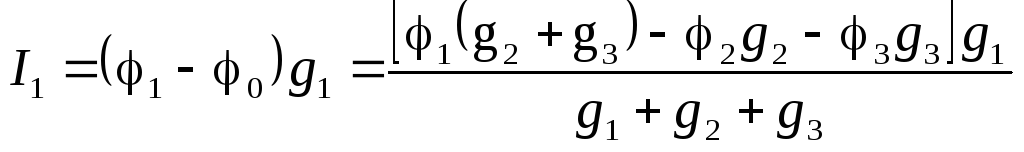. (1.12)

С другой стороны, для треугольника в соответствии с обозначениями на рис. 1.12

. (1.13)

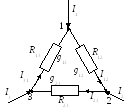
Рис.1.12

Так как ток I₁ в схеме рис. 1.11 равен току I₁ в схеме рис. 1.12 при любых значениях потенциалов ₁, ₂ и ₃, то коэффициент при ₂ в правой части формулы (1.13) равен коэффициенту при ₂ в правой части уравнения (1.12), а коэффициент при ₃ в правой части формулы (1.13) равен коэффициенту при ₃ в правой части уравнения (1.12). Следовательно,

(1.14)

. (1.15)

Аналогично

. (1.16)

Формулы (1.14), (1.15) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды.

Из уравнений (1.14)—(1.16) выразим сопротивления лучей звезды ;;через сопротивления сторон треугольника:

; ;.

С этой целью запишем дроби, обратные уравнениям (1.14)-(1.16):

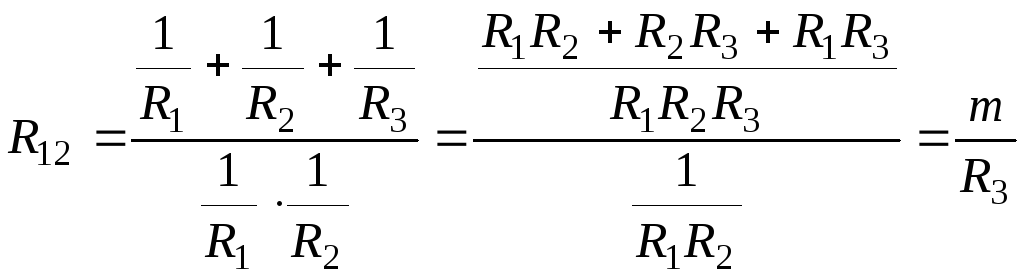; (1.17)

, (1.18)

где

; (1.19)

. (1.20)

Подставив формулы (1.17), (1.19) и (1.20) в выражение (1.18), получим

.

Следовательно,

.

Подставив m в выражение (1.19), найдем

. (1.21)

Аналогично:

; (1.22)

. (1.23)

Структура формул (1.21)—(1.23) аналогична структуре формул (1.14) -(1.16).