ЛекцияАИУС2011

71

(1)1

8

t2

Позиции 1, 2 описывают условия запуска двигателя вниз, вверх соответственно. Наличие маркеров в позиции 3 и 4 обозначает замкнутость контакта Z1, а

в позициях 5 и 6 – контакта Z2.

Маркер в позиции 7 обозначает 4(4) 3(3) замкнутость либо Z1 либо Z2. Позиция 8 моделирует остановку двигателя, а позиция 9,10 – движение вниз или вверх соответственно. Этим позициям приписано время задержки маркера, равное времени перемещений между крайними положениями.

Пусть маркеры находятся в позициях 5, 6, 8. Запуск двигателя (вниз) может произойти только после появления маркера в позиции 1. При срабатывании перехода t1, маркер появляется в позиции 9, что означает движение захватывающего центр. вниз. После срабатывания перехода t3 (замыкание контакта Z1) и перехода t5, маркеры поступают в позиции 3, 4, 8. Полученная маркировка является исходной для запуска двигателя вверх. Позиции 4, 6, 7 введены для имитации собственно процессов упр. двигателя Z, а позиции 3 и 5 – для имитации процесса управле-

72

ния манипулятором. Работа двигателя X также можно смоделировать сетью Петри. При этом позиции 1, 9, 4,3 моделируют движение вправо, а позиции 2, 10, 5, 6

– влево. Функционирование сети при моделировании работы двигателя X аналогично описанному выше (для двигателя Z). Модель работы двигателя G представлена на рисунке:

Позиции 11, 12 моделируют состояние *захватное устройство открыто* 13, 14 – *захватное устройство открыто*. Маркеры в позициях 15, 16 – команды на выполнение одного из этих состояний.

Позиции 17, 18 соответствуют переходным режимам из одного состояния в другое. Этим позициям приписано время задержки, равное времени нахождения захватывающего устройства в соответствующих состояниях. Пусть маркеры находятся в позициях 13 и 14 (захватывающее устройство открыто). Приход маркера в позицию 15 заставляет сработать переход t1, моделирующий начало захвата. В результате срабатывания t1 маркер появляется в позиции 18 (переход из состояния *открыт* в состояние *закрыт*). Срабатывающей затем переход t3 переводит захватывающее устройство в закрытое состояние (маркеры в позициях 11, 12). Эта маркировка является исходной для запуска двигателя, открывающего имитации собственно процессов управления двигателя G, а позиции 11, 15 – для имитации процесса управления манипулятором.

Модель функционирования манипулятора изображена на рисунке:

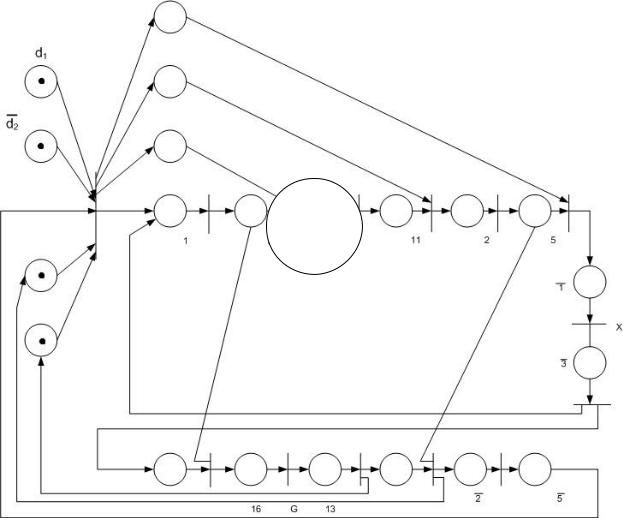
73

Начальная маркировка сети соответствует начальному состоянию манипулятора (x1, z2, g2) и условием: деталь находится на площадке A, и площадка B свободна. Из исходного положения работа манипулятора осуществляется по циклу: *вниз за деталью*, *взять деталь*, *вверх с деталью*, * вправо с деталью*, *вниз с деталью*, * открыть захватывающее устройство*, *вверх без детали* и т.д. Повторение цикла осуществляется в том случае, если на месте A появится новая деталь, а с места B будет убрана деталь, перенесенная туда раньше. Сеть, приведенная на рисунке, является иерархической. Двигатели Z, X, G в сети моделируются наборами переходов, которые обозначены соответствующими символами. Любой из переходов Z, X, G с инцидентными ему входными и выходными позициями интерпретируется как процесс, происходящий в двигателях Z, X, G. Поэтому при необходимости указанные переходы могут быть заменены моделями, изображенными выше. Путем композиции строится общая модель. Описанная модель манипулятора служит для разработки имитационных моделей производственных систем, содержащих манипулятор.

3.4. Метод машинного имитационного моделирования.

74

Имитационные модели позволяют рассматривать процессы, происходящие с тех. сист., практически на любом уровне детализации. Для машинной реализации имитационной модели, необходимо построить соответствующий моделирующий алгоритм, воспроизводящий в некотором масштабе времени процесс функционирования исследуемой системы с той степенью детальности, которая необходима разработчику (исследователю).

Термин *имитационное моделирование* не очень удачен, т.к. имитация сама по себе есть моделирование, а моделирование – имитация. Тем не менее, этот термин устойчиво *прижился* со спец. тех. литературе и часто отождествляется с терминами *машинная имитация*, *машинный имитационный эксперимент*, *имитационный эксперимент на ЭВМ*, *статистическое моделирование*. Употребление последнего термина обусловлено тем, что статистическое моделирование, как метод машинной реализации имитационных моделей систем, подверженных случайным воздействиям, в настоящее время наиболее употребим, хотя в детерминированных случаях, имитационные модели реализуются и другими методами.

Статистическое моделирование представляет собой численный метод, дающий частное решение, отвечающее фиксированным значениям параметров системы, входной информации и начальным условиям. В основе его лежит процедура, применяемая для моделирования случайных величин и функций и носящая название метода статических испытаний (метод Монте-Карло).

Общая схема метода Монте-Карло может быть записана в виде:

Результат ищется как математическое ожидание некоторой случайной величины Y, которая чаще всего является неслучайной функцией случайной величины X, имеющей распределение p(x). Нестрогое выражение *случайная величина X имеет распределение p(x)* и запись X ~ p(x) означают для непрерывной случайной величины, что ее плотность вероятности равна p(x); для дискретной случайной величины функции p(x) надо понимать как Ф вероятности. Для дискретной случайной величины, интеграл заменяется суммой. М – это число опытов. После того как

требуемой величины, зависящей от допустимой погрешности и коэффициента до-

верия.

H

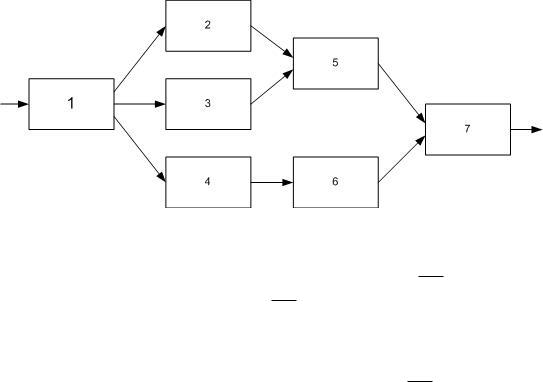
Проиллюстрируем суть метода Монте-Карло простым примером. Пусть требуется оценить надежность системы:

75

Система выполняет свою функцию, если работают цепочки блоков: 1, 2, 5, 7; 1, 3, 5, 7; 1, 4, 6, 7. Какие-то блоки могут отказать. Каждый блок характеризуется временем безотказной работы Ti(i=1, 7). Пусть задана плотность распределения pi(Ti) (i=1, 7). Какова надежность в целом? Рассмотрим случайную величину:

γ=min{T1, max[min(T4, T6), min[max[min(T2, T3), T5]], T7} , γ – время безотказной работы системы.

В одном опыте разыгрывается значение Ti(i=1, 7) в соответствии с

pi(Ti) (i=1, 7). Через полученные реализации Ti по формуле( см.выше) вычисляем реализацию γ. Один опыт дает одну реализацию γ. Проводим М опытов (испытаний), получаем *статистический* материал (выборку). Берем среднее арифметическое времени безотказной работы системы γср в качестве оценки надежности системы. При необходимости можно построить и закон расп. сл. величину γ.

Таким образом, испытания реальной системы заменены на испытание мат. модели. Каждое испытание сопровождают расчетом. Поэтому имитационное моделирование и называют численным экспериментом на ЭВМ с мат. моделью (модель выступает как объект испытания). При реализации испытания возможны и логические операции. И расчетные и логические операции реализуются на ЭВМ с помощью соответствующих алгоритмов, которые в совокупности составляют определенный выше моделирующий алгоритм.

Структурная схема эксперимента по имитационному моделированию показана на рисунке:

76

3.2 Модель управления обслуживанием и очередями.

Типичная ситуация, в которой возникает задача обслуживания, выглядит следующим образом: есть обслуживающее устройство, и на него поступает поток заявок, которые необходимо выполнить.

Возможны две ситуации:

1) число заявок слишком велико и обслуживающее устройство не успевает своевременно обслуживать все заявки, что приводит к образованию очереди и, как следствие, возникновению экономических потерь из-за ожидания заявок в очереди; 2)на обслуживающее устройство поступает недостаточное количество заявок, в этом случае потери образуются из-за простоя обслуживающего устройства.

Задача состоит в том, чтобы применительно к данному потоку заявок так подобрать параметры

77

обслуживающего устройства, чтобы минимизировать суммарные потери от простоя обслуживающего устройства и ожидания заявок в очереди.

Задачи массового обслуживания имеют очень широкое распространение: обслуживание покупателей в магазине, медицинское обслуживание, продажа билетов, выдача справок, морские и авиапорты и т.д.

Применительно к промышленному производству задачи массового обслуживания возникают при ремонте оборудования, обслуживании множества станков бригадой рабочих-наладчиков, выдаче материалов и инструментов со склада и т.д.

В основном производственные задачи массового обслуживания возникают и решаются в подсистемах технического обслуживания производства, сбыта и реализации продукции.

Рассмотрим основные понятия и математическую постановку задачи массового обслуживания, следуя такой схеме:

1)основные характеристики и свойства потока заявок

2)основные характеристики обслуживающего устройства 3)определение оптимальных характеристик обслуживающего устройства при данном потоке заявок.

1. Характеристики и свойства потока заявок.

Процесс возникновения заявок имеет случайный характер, и потому поток заявок описывается вероятностными характеристиками, из которых важнейшими являются интенсивность потока λ,

1⁄ед. вр.(произвольная единица времени), то есть среднее количество заявок за отрезок времени

Т. Наиболее разработана теория для простейшего потока, который определяется тремя условиями:

1.Стационарность, т.е. λ не зависит от текущего времени t.

2.Отсутствие последствия, т.е. число заявок за выбранный отрезок времени Т не зависит от числа заявок, обслуженных в предыдущем промежутке времени.

3.Ординарность, т.е. очень малый промежуток времени поступает не более одной заявки. Показано, что для простейшего потока дискретная случайная величина X (число заявок за время Т) имеет закон распределения Пуассона:

Чем меньше значение а, тем более ассиметричный вид имеет Р (X=k). Для распределения Пуассона:

Тогда для простейшего потока заявок справедливы следующие результаты: 1. Среднее число заявок за время T

̅[ ]

2.Вероятность того, что при интенсивности λ за время T поступит ровно k заявок, равно

На первый взгляд, простейший поток обусловлен жесткими ограничениями, однако, как показывают многочисленные исследования, большинство реальных ситуаций, порождающих очереди, характеризуется простейшими потоками заявок; в частности, все перечисленные выше примеры производственных задач массового обслуживания имеют пуассоновский закон распределения числа заявок.

Хотя, конечно, встречаются случаи, когда условия простейшего потока не выполняются; например, неординарный поток соответствует обслуживанию коллективных заявок, в которых

( ).

Поскольку возникновение заявок случайно, случайной величиной будет и интервал между соседними заявками. Определим закон распределения непрерывной случайной величины :

78

Вероятность того, что не меньше T, равна вероятности того, что за время T не возникнет ни одной заявки, т.е.

При текущем времени t выражение (*) представляет собой интегральный закон распределения случайной величины :

Это так называемый экспоненциальный закон распределения. Для экспоненциального закона распределения среднее значение интервала между соседними заявками ̅̅̅ и дисперсия [ ] равны:

̅̅̅[ ] 1 , ед. вр. [ ] 1

Экспоненциальный закон распределения интервалов между заявками однозначно следует из пуассоновского распределения потока заявок. Поэтому экспериментальное установление соответствия распределения реального потока заявок по закону Пуассона можно проводить либо по наблюдениям над частотой поступления заявок, либо по наблюдениям за интервалами между заявками.

Значение параметра λ для исследуемого потока можно определить экспериментально в результате подсчёта числа поступивших заявок n за достаточно большой период времени T. Тогда значение λ берётся равным:

⁄

2. Характеристика обслуживающего устройства.

Обслуживающее устройство характеризуется временем выполнения заявок τ. Обычно рассматривается два случая:

1) время выполнения любой заявки одинаково; 2)время выполнения заявки зависит от характера заявки и является случайной величиной.

Второй случай более соответствует реальному положению вещей. При этом обычно принимают, что распределение τ подчиняется экспоненциальному закону, т.е. плотность вероятности τ имеет вид:

( ) , где - параметр времени обслуживания.

Экспоненциальный закон времени обслуживания хорошо согласуется с действительным положением вещей, когда основная масса заявок выполняется быстро, а продолжительное обслуживание требуется сравнительно редко.

Из свойств экспоненциального распределения следует, что среднее время выполнения заявки, ед. вр., равно:

где – в 1⁄ед. вр.

При анализе реального обслуживания устройства необходимо экспериментально проверять соответствие экспоненциального закона распределения действительному и определить значение параметра .

Кроме закономерностей, описывающих поток заявок и функционирование обслуживающего

79

устройства, для оптимального расчёта системы массового обслуживания необходимо задаться

дисциплиной обслуживания.

Дисциплина обслуживания определяет порядок, в котором обслуживающее устройство обрабатывает поступающие заявки.

Возможны два основных случая:

1.Заявка отвергается, если она поступила в момент, когда обслуживающее устройство занято выполнением предыдущей заявки. По такому принципу работают, например, телефонные станции.

2.Заявка ставится в очередь, если обслуживающее устройство занято. Для задач массового обслуживания производственного типа характерен именно этот случай.

Заявки из очереди могут выполняться в порядке их поступления или в соответствии с присвоенными приоритетами.

В дальнейшем мы будем рассматривать обслуживающее устройство с очередью без приоритетов.

Прежде чем перейти к определению оптимальных параметров обслуживающего устройства при заданном пуассоновском потоке заявок интенсивности λ, введём коэффициент

⁄

Этот вывод легко понять, если учесть, что 1⁄ есть средняя длительность выполнения заявки, а 1⁄ - средняя длина интервала между соседними заявками. Если 1⁄ 1⁄ , что соответствует

1, то одно обслуживающее устройство не справляется с потоком интенсивности λ и очередь будет неограниченно расти. Эти рассуждения можно повторить, если рассмотреть λ как скорость поступления заявок, а µ - скорость выполнения заявок. Коэффициент r можно трактовать как меру загруженности обслуживающего устройства, и на первый взгляд кажется естественным желанием так выбрать параметр µ, чтобы обслуживающее устройство при ситуации, образуемой случайным потоком заявок, всегда было в действии, т.е. чтобы коэффициент был равен или близок к единице.

Однако такое решение является экономически неоптимальным в силу причин, которые будут рассмотрены ниже.

3. Определение оптимальных характеристик обслуживающего устройства.

В теории массового обслуживания показано, что для пуассоновского потока заявок и экспоненциального распределения времени обслуживания вероятность появления очереди l длиной k равна: