ЛекцияАИУС2011

61

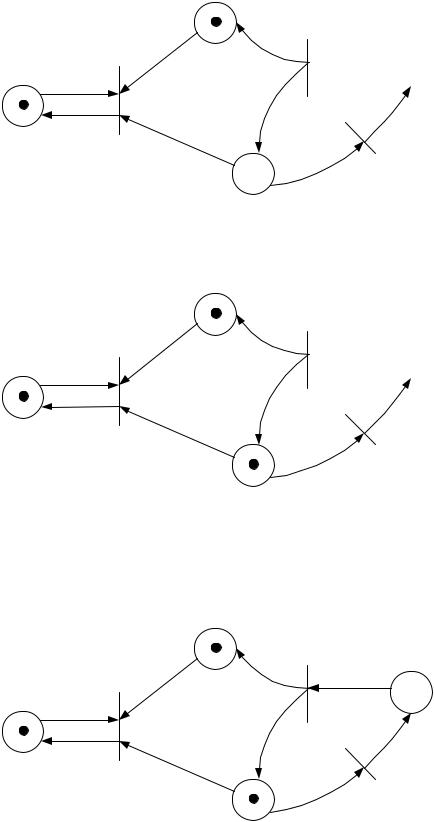
Рассмотрим пример:

t3

p3

a) Исходная сеть Петри.

t3

p3

63

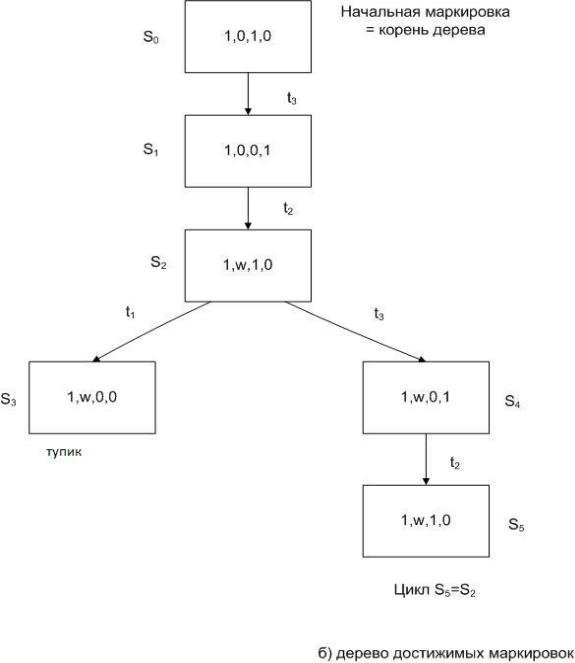
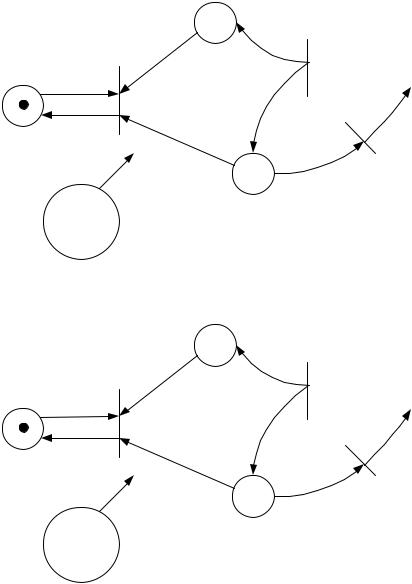
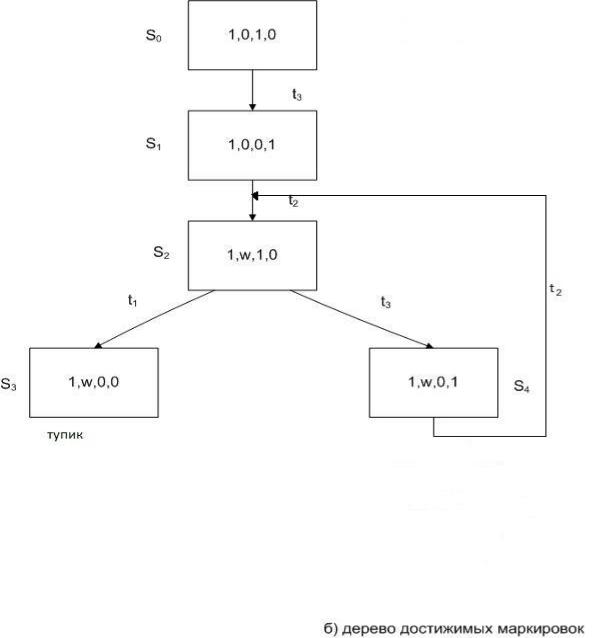
В качестве примера рассмотрим сеть Петри, изображенную на рис.а) с начальной маркировкой S0=(P10, P20, P30, P40,)=(1,0,1,0). Примем начальную маркировку в качестве корня дерева (рис. б)). В ней возбужден только один переход t3 (Переход возбужден, если все входные позиции переходов имеют метки).

t3

p3

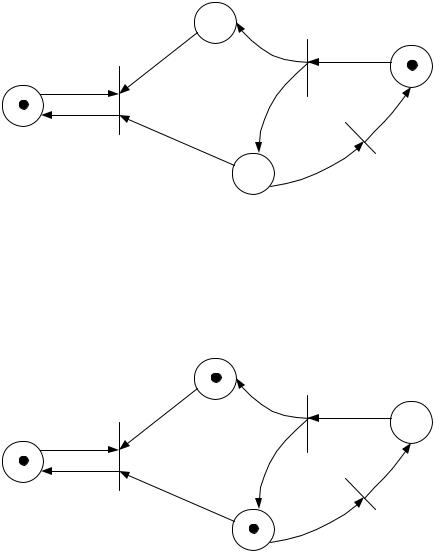
Новой вершиной, соответствующей срабатыванию t3, будет вершина с маркировкой S1=(1, 0, 0, 1). Дуга из S0 к S1 отмечается t3. В маркировке S1 может сработать переход t2, порождая маркировку S2=(1, 1, 1, 0).

t3

p3

Поскольку все компоненты S2 не меньше соответсв. компонент S0, а вторая компонента строго больше, то на место второй компоненты в маркировке S2 по-

мещается символ Ѡ, т.е. S2=(1, Ѡ, 1, 0). Это отражает тот факт, что мы можем по-

вторить из S0 последовательность t3, t2 неограниченное число раз и сделать число точек в позиции P2 сколь угодно большим. В маркировке S2 возбуждены два перехода – t1 и t3, которые при срабатывании дают две новые вершины с маркировками S3=(1, Ѡ, 0, 0) и S4=(1, Ѡ, 0, 1). Первая (S3) является тупиковой, поскольку функция б(S3,t) не определена для всех t. Во второй (S4) возбужден переход t2,

66

Сеть является живой, если на этом выполняются следующие два условия:

1.Граф должен быть сильно свзязан ( две вершины в этом графе долж-

ны быть взаимно достижимы).

2.На дугах графа должны быть указаны все переходы.

Нетрудно убедиться, что в нашем примере, сеть Петри неограниченная и неживая. Таким образом, для распознавания правильности произвольной сети Петри с заданной начальной маркировкой, следует для нее построить дерево достижимых маркировок, превратить его в граф с циклами и исследовать последний на сильную связанность. Проверка графа на сильную связанность требует построения для каждой его вершины своего дерева достижимости. Это трудоемкая задача. Нужны новые методы.

Опыт использования обычных сетей Петри показал высокую трудоемкость

67

анализа сетей большой размерности на наличие свойств достижимости, живости, ограниченности и т.д. Это явилось причиной разработки подклассов сетей Петри, в которых вводятся определенные ограничения на структуру сети, что позволяет использовать более приятные алгоритмы для ее анализа. Одним из таких подклассов является раскрашенные сети Петри.

3.2.Раскрашенные сети Петри.

Раскрашенные сети Петри по своим возможностям эквивалентны обычным сетям. Введение в сети еще одного множества – раскрасок (цветов) меток позволяет уменьшить размерность графа при моделировании сложных систем.

Меткам раскрашенной сети Петри приписывают атрибуты, которые называют цветами. Правила возбуждения переходов дополняются условиями, предполагающими выбор меток определенных цветов из входных позиций. Срабатывание переходов сопровождается посылкой в выходную позицию меток с задаваемыми значениями цветов.

Рассмотрим пример:

68

P9

P2

P10

На рисунке приведена модель процессов в двухстаночной системе, обслуживаемой роботом, на которой множество атрибутов, цветов, связываемых с метками и дугами сети, принято:

P1, P2 – бункеры для заготовок;

P3, P4 – конец загрузки, запуск обработки;

69

P5, P6– конец обработки, запрос загрузки; P7, P8– бункеры для готовых изделий;

P9, P10 – семафоры, исключающие попытки загрузить еще не разгруженные станки.

В сети раскрашена метка, имитирующая работу робота, и дуги на маршруте робота. Прочие дуги, а также метки-изделия и метки управления не раскрашены. Начальный цвет метки в P0 равен C1, а дуга (p0,t1) окрашена в C1. Условие для возбуждения перехода t1 выполняется. После срабатывания t1 в P0 метка возвращается, уже имея цвет C2, поскольку дуга (p0,t1) раскрашена в цвет C2. Раскрашивание дуг обеспечивает возбуждение только одного из переходов, следующих за P0 при любом состоянии системы. При данной раскраске маршрут робота представлен последовательностью срабатывающих переходов t1, t2, t5, t6, т.е. происходит загрузка первого станка, затем загрузка второго, после чего следует из разгрузка и цикл повторяется. Цвет метки можно обозначать одной из фигур { , , }.

3.3. Имитационные модели для анализа функционирования.

При построении моделей используется два принципа: модульности и структурного подобия.

Принцип модульности заключается в следующем. Моделируемый объект делится на фрагменты (модули), для каждого из которых строится модель. Затем модели модулей агрегируются для получения обобщенной модели технической системы. Модуль должен представлять собой достаточно автономный, с технологической точки зрения, объект. Под автономностью здесь понимается относительно небольшое число связей данного объекта с другими. Заметим, что выделения модулей и построение их моделей представляет собой творческий процесс, который трудно или невозможно описать формальными правилами. Приведенные ниже модели и описание процесса их построения иллюстрируют некоторые приемы выделения модулей и их описания на языке Петри.

Принцип структурного подобия заключается в том, что каждому значимому структурному элементу объекта ставится в соответствие набор позиций сети, при этом текущая разметка данного набора позиций однозначно характеризует определенное состояние элемента.

Рассмотрим модель манипулятора. Моделируется манипуляфтор, предназначенный для транспортировки изделия с площадки A на площадку B.

70

Манипулятор имеет две степени свободы: он может перемещаться вправовлево и вверх-вниз с помощью двигателей горизонтального перемещения Z и вертикального перемещения X. Его захватное устройство закрывается и открывается посредством вращения двигателя G. Движение манипулятора по вертикали ограничено координатами Z1 и Z2, а по горизонтали координатами X1 и X2. При достижении этих координат, соответствующие контакты замыкаются. При захвате детали замыкается контакт g2, а при отпускании – контакт g1. При наличии детали на площадках A и B замыкаются соответственно контакты d1 и d2. Транспортировка детали возможна, если d1 замкнут (деталь находится на площадке A), а d2 разомкнут (площадка B свободна). В начальном положении захватного устройства контакты x1, z2 и g1 замкнуты (захватное устройство закрыто, координаты x1,z2). Двигатель Z после пуска вниз или вверх работает до полной остановки в положении Z2 или Z1. Одним из вариантов модели, описывающей его функционирование, является сеть Петри, изображенная на рис: