
ЛекцияАИУС2011
.pdf51
Раздел III. Модели технических систем.
3.1. Сетевые модели
Графические методы в исследованиях, проектировании, программировании получили широкое распространение в связи с широкими возможностями графических терминалов.
Графические, структурные или диаграммные представления широко используются в технике. Какой бы сложной не была схема, ее целесообразно видеть.
Сети Петри – самый распространенный в настоящее время формализм, описывающий структуру и взаимодействие параллельных процессов. Теория сетей Петри развивается в нескольких направлениях, серди которых – математическая теория сетей, структурная теория сетей, приложения к задачам параллельного программирования, применение сетей Петри как основы для создания моделей дискретных динамических систем.
Среди достоинств аппарата сетей Петри можно указать следующее:
1.Сети Петри позволяют моделировать асинхронность и недетерминизм параллельных независимых событий, параллелизм конвейерного типа, конфликтные взаимодействия между процессами.
2.Сети Петри обладают большой выразительной мощностью.
3.Сети Петри допускают произвольную интерпретацию элементов модели как в смысле типа выполняемого фрагмента (выражения, операторы, подпрограммы, аппаратные функциональные преобразования информа-
ции) так и по уровню абстракции.
Таким образом, сети Петри позволяют производить иерархическую детализацию программных и аппаратных подсистем модели.
Рассмотрим основные элементы аппарата сетей Петри. Формально сеть Петри задается как
N = (В, D, Ф, Н),
где:
В – конечное множество символов, называемых позициями В ≠ Ǿ; (состояний, мест)
Д – конечно множество символов, называемое переходами D ≠ Ǿ; (событий)
B∩D = Ǿ
Ф: B ᵡ D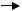 {0,1} – прямая функция инцидентности Н: D ᵡ В
{0,1} – прямая функция инцидентности Н: D ᵡ В  {0,1} – обратная функция инцидентности.
{0,1} – обратная функция инцидентности.
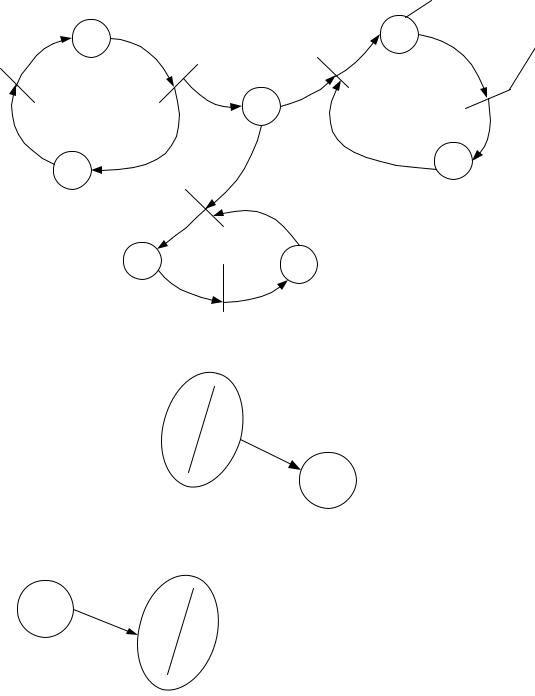
Указанные четыре множества определяют структуру сети Петри. Такое задание удобно для формального рассмотрения, но не обладает наглядностью, поэтому сеть Петри обычно представляют двудольным графом с двумя типами вершин:
|
|
52 |
|
b |
1 |
b4 |
условия |
|
|
||
|
|
d3 |
события |
|
|
|
|
|
|
d2 |
|
|
|
b3 |
|
|
|
|
d4 |
b2 d5 b5
b7 b6
d6
dj
|
bi |
H(dj, bi)=1 |
H(dj)=1 |
bi |
dj |
|
Ф(dj)=1
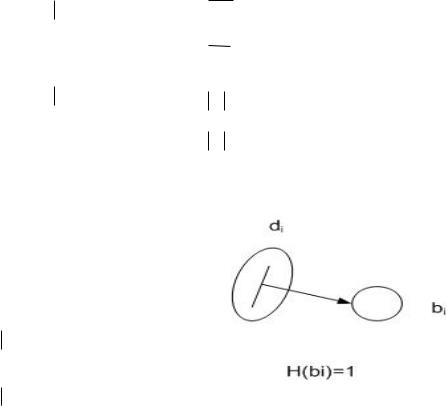
Вершины – позиции – изображаются кружками, а вершины переходы – черточками.
Из вершины – позиции bᵢ в вершину – переход dj ведет дуга, если и только если Ф(bᵢ, dj)=1; из вершины – перехода dj в вершину позицию bᵢ ведет дуга, если и
53
только если Н(dj, bᵢ)=1.
Для каждого перехода dj Д можно определить множество входных по-
зиций перехода Ф(dj) и выходных позиций перехода Н(dj) как:
Ф(dj) = { bᵢ B Ф(bᵢ, dj)=1} где: i= 1, n;
J= 2,m;
Н(dj) = { bᵢ B Н(dj, bᵢ)=1} где: n= В
m= D
Аналогичным образом вводится определение множества входных переходов позиции bᵢ - Н(bᵢ) и множества выходных переходов данной позиции Ф(bᵢ)
Н(bi) = {dj D Н(dj, bᵢ)=1} Ф(bi) = {dj D Ф(bᵢ, dj)=1}
Так например сеть Петри, представленная на рисунке, может быть представлена как:
N= (В, D, Ф(dj) Н(dj) )
B= {b1, b2, b3, b4, b5, b6, b7}
D= {d1, d2, d3, d4, d5, d6}
входные позиции переходов |
выходные позиции переходов |
Ф(d1)= {b2}; |
H(d1)= {b1}; |
Ф(d2)= {b1}; |
H(d2)= {b2, b3}; |
Ф(d3)= {b3, b5 }; |
H(d3)= {b4}; |
Ф(d4)= {b4}; |
H(d4)= {b5}; |
Ф(d5)= {b3, b7}; |
H(d5)= {b6}; |
Ф(d6)= {b6}; |
H(d6)= {b7}; |
Ф(b1)= {d1}; |
|
H(b1)= {d2}; |
|
Ф(b3)= {d2}; |
|
H(b3)= {d3, d5}; |
|
54
Наибольшее применение сети Петри нашли для моделирования систем с дискретными событиями, которые могут происходить одновременно и параллельно. При моделировании отражаются два аспекта системы: события и условия. Позиции сети соответствуют условиям, а переходы событиям. Функции инцидентности отражают связи между условиями и событиями в системе.
Приведенное выше определение сети Петри может использоваться для статики моделируемой системы (взаимосвязи событий и условий), но не позволяет моделировать динамику функционирования.
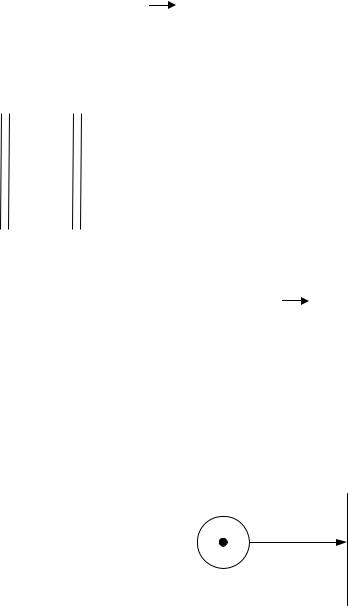
Для представления динамических свойств, вводится функция размети (маркирования) сетей:
M:B {0, 1, 2, . . .}
Спомощью функции М позиции сети помечаются целыми неотрицательными числами. При графическом задании сети Петри, разметка отображается помещением внутрь вершин позиций соответствующего числа точек, называемых метками. Маркирование сети представляется вектором
m(b1) |
|
|
М= m(b2) |
,где m(bi) – число меток в позиции bi |
|
. |
|
|
. |
|
|
m(bn) |
|
|
Сеть Петри функционирует, переходя от разметки к разметке. Начальная |
||
разметка обозначается как M0: B |
{0, 1, 2 . . .}. Смена разметок переходит в резуль- |
|
тате срабатывания одного из переходов di D сети.
Говорят, что переход di возбуждается маркированием M и может сработать, если все выходные позиции перехода di имеют метки.
Формальная запись условия возбуждения имеет вид :
bi B [m(bi) – 0(bi, dj) 0], где 0(bi, dj) – дуга, соединяющая i позицию с j переходом, сравнивает число меток в bi с числом дуг между bi и dj.
m(bi) больше числа дуг (bi, dj), то m(bi)- (bi, dj) 0
di
Срабатывание перехода dj приводит к тому, что его входные позиции теряют столько меток, сколько дуг ведет из этой позиции к переходу dj, а каждая выходная
позиция приобретает столько меток, сколько дуг идет от данного перехода dj к каждой из его выходных позиций.
Сеть Петри, в которой используется функция разметки, называется разметочной сетью Петри и задается набором:
55
Nm=(B, D, Ф, H, Mo)
Если в сети задано начальное маркирование, при каждом хотя бы один переход возбужден, то в ней начинается движение меток. Если в сети N одновременно возбуждено несколько переходов, то порядок их срабатывания не определен, и, соответственно, может быть представлено несколько последовательностей срабатывающих переходов d.
Рассмотрим пример:
b |
1 |
b4 |
условия |
|
|
d3 |
события |
|
|
|
|
d1 |
|
d2 |
|
|
b3 |
|
|
|
|
|
|
|
|
|
d4 |
b2 |
|
|
|
|
|
d5 |
b5 |
|
|
|
разметка b7
b6
d6 |
Mo |
|
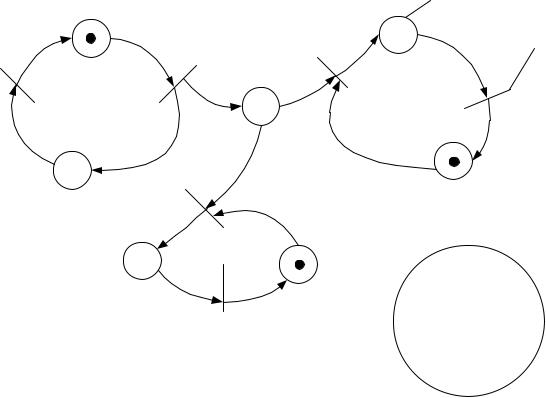
M0={1, 0, 0, 0, 1, 0, 1} (все входные позиции перехода имеют метки).
При такой начальной разметке единственным готовым к срабатыванию является переход d2.
Срабатывание его ведет к смене разметки:
56
b1 |
b4 |
условия |
|
d3 |
события |
|
|
|
d1 |
d2 |
|
b3 |
|
|
|
|
|
|
|
d4 |
b2 |
|
|
|
d5 |
b5 |
|
|
|
|
b7 |
разметка |
|
|
|
|
b6 |
M1 |
|
d6 |
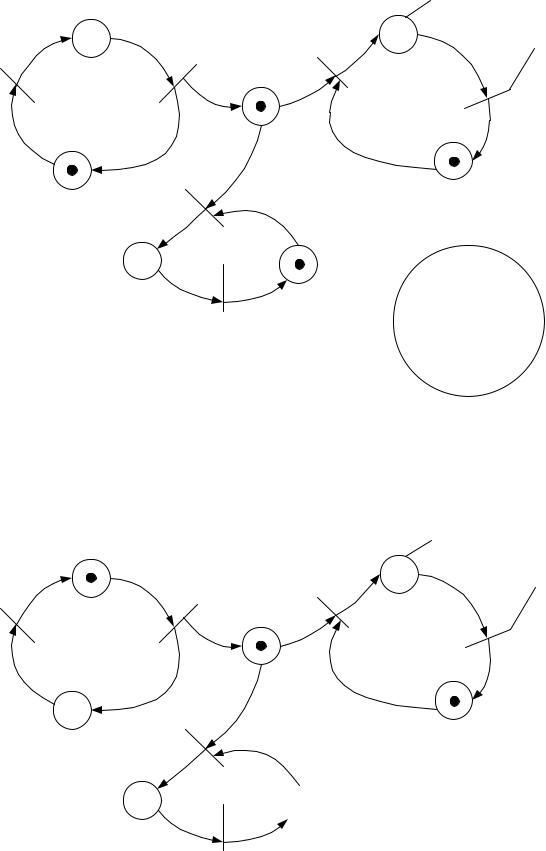
M1={0, 1, 1, 0, 1, 0, 1} |
|
|
При разметке M1 |
возможно срабатывание трех переходов: d1, d3, d5. |
|
В зависимости от того, какой из переходов сработал первым, получается од- |
||
на из трех возможных разметок: |
|
|
b1 |
b4 |
условия |
|
d3 |
события |
|
|
|
d1 |
d2 |
|
b3 |
|
|
|
|
|
|
|
d4 |
b2 |
|
|
|
d5 |
b5 |
|
|
|
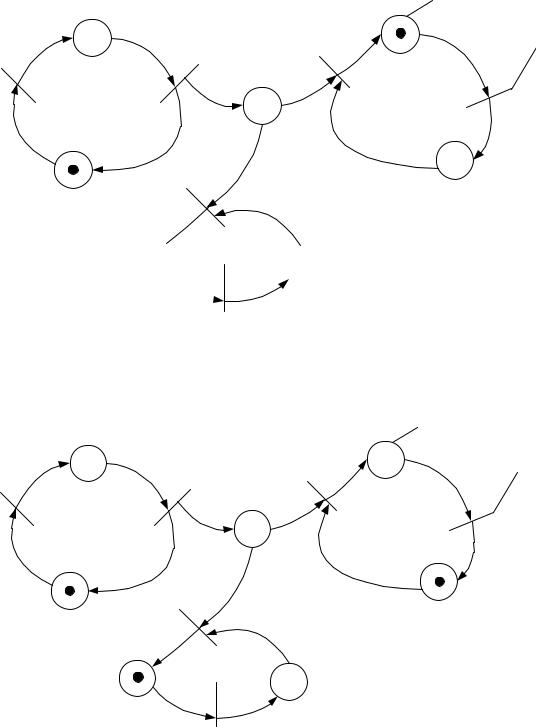
 b7 (d1)
b7 (d1)
b6
d6
|
|
57 |
|
b |
1 |
b4 |
условия |
|
|
||
|
|
d3 |
события |
|
|
|
|
d1 |
|
d2 |
|
|
b3 |
|
|
|
|
|
|
|
|
|
d4 |
b2 |
|
|
|
|
|
d5 |
b5 |
|
|
|
 b7 (d3) b6
b7 (d3) b6 
d6
b |
1 |
b4 |
условия |
|
|
d3 |
события |
|
|
|
|
d1 |
|
d2 |
|
|
b3 |
|
|
|
|
|
|
|
|
|
d4 |
b2 |
|
|
|
|
|
d5 |
b5 |
|
|
|
(d |
) |
b7 |
5 |
b6 |
|
d6 |
|
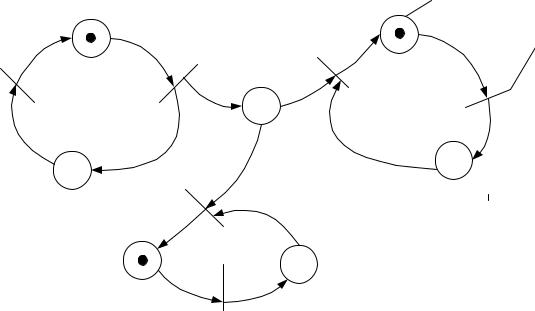
Кроме того возможно срабатывание одной из пары переходов (d1, d3), (d1, d5), и (d3, d5) и всех трех переходов (d1, d3, d5):
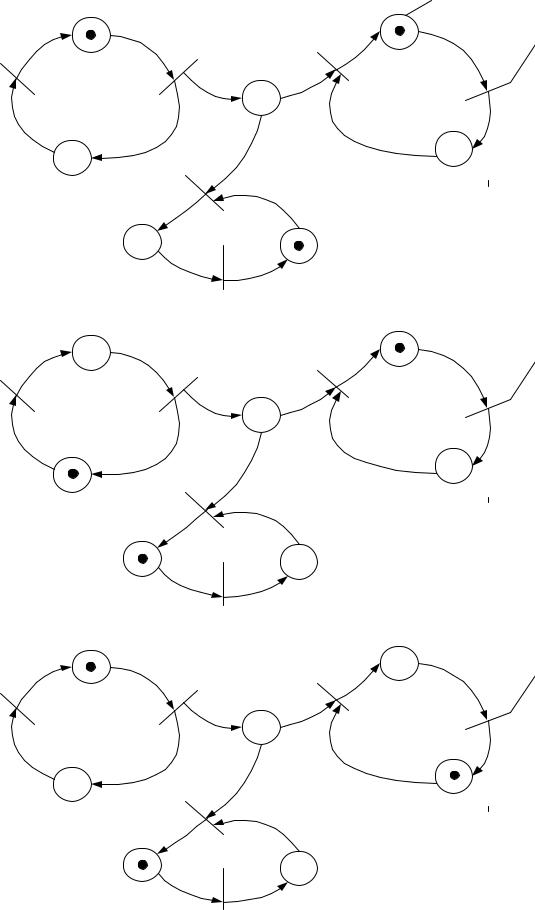
58
|
b1 |
|
|
d3 |
|
d1 |
d2 |
|
b3 |
||
|
b2
d5
b7
|
b6 |
|
|
d6 |
|
|
b1 |
|
|
d3 |
|
d1 |
d2 |
|
b3 |
||
|
b2
d5
b7
b6
d6
b1
|
d3 |
|
d1 |
d2 |
|
b3 |
||
|
b2
d5
b7
b6
d6
b4 |
условия |
события
d4
b5
(d |
, d |
) |
1 |
3 |
|
b4  условия
условия
события
d4
b5
(d3, d5)
b4  условия
условия
события
d4
b5
(d1, d5)
|
|
59 |
|
b |
1 |
b4 |
условия |
|
|
||
|
|
d3 |
события |
|
|
|
|
d1 |
|
d2 |
|
|
b3 |
|
|
|
|
|
|
|
|
|
d4 |
b2 |
|
|
|
|
|
d5 |
b5 |
|
|
|
b7 |
(d1, d3, d5) |
b6
d6
Функционирование сети Петри продолжается до тех пор, пока существует хотя бы один возможный переход.
Важной особенностью модели сети Петри является простота иерархического построения модели. Каждая сеть может рассматриваться как макропереход или макропозиция модели более высокого уровня. С другой стороны переход или позиция могут детализироваться в форме отдельной подсети для более углубленного исследования аспектов моделируемой системы.
Обычные размеченные сети Петри, как они были определены выше, пригодны для описания событий произвольной длительности. Модель в этом случае отражает только порядок наступления событий в рассматриваемой системе.
Функционирование сети Петри происходит недетермировано в том случае, когда возникает разметка соответствующему возбужденному состоянию двух или более переходов.
Время срабатывания перехода модели на основе сети Петри принимается бесконечно малым и вводится предположение о том, что вероятность двух или более одновременных событий равна нулю. Тот факт, что обычные сети Петри не отражают временных параметров моделированной системы, являются существенным ограничением при их использовании в качестве моделей. Для устранения этих ограничений разработаны различные расширения сетей Петри.
Модель на основе сети Петри дает возможность анализа системы при наличии желательных или нежелательных свойств. Основные направления анализа для обычных сетей Петри следующие:
1.Проблема достижимости. В заданной сети Nm с начальной разметкой M0 требуется решить вопрос, достижима ли принципиально некоторая разметка M, из M0. В приложении к моделированию систем. Эта проблема интерпретируется как возможность достижения определенного состояния системы. При анализе используется понятие множества всех достижимых в Nm разметок, которое обозначается
R(Nm).
2.Свойство живости. Под живостью перехода сети Петри понимают прин-

60
ципиальную возможность его срабатывания в некоторой Nm при начальной разметке М0. Сеть Петри определяется как живая, если все ее переходы живые. Анализ модели на свойство живости позволяет выявить неживые переходы, т.е. невозможные события в моделируемой системы.
Mi, Mj R(M0) [Mj M0]
t T Mg, Mh R(S0)[ Mg t Mh]
Для любой пары маркировок принадлежащих множеству R(M0) имеет ме-
сто переход из Mi в Mj и для любого перехода из t в множестве R(M0) такая пара маркировок Mg, Mh, что Mg t Mh.
3.Ограниченность сети. Позиция bi в Nm называется K – ограниченной, ес-
ли существует такое целое число K, что M(bi) K для любой разметки M в R(Nm). Если в Nm bi B{M(bi) K } для M R(Nm), т.е. Nm называется K – ограниченной. Если K=1, то сеть называется безопасной.
4.Безопасноть сети. Сеть Nm называется безопасной если выполняется условие M(b) R(Nm){ bi M(bi) 1}; i=1n; n= B . То есть безопасной являет-
ся такая сеть Петри, в которой ни при каких условиях не может появиться более одной метки в каждой из позиций (K – ограниченность равна 1).
Для моделей реальных систем анализ на ограниченность (безопасность) позволяет проверить возможность функционирования системы в некотором стационарном режиме без перехода заданного предела по числу объектов в отдельных подсистемах.
5.Свойство сохранения. Сеть Nm называется сохраняющей если
∑ M(bi)=const (bi B) для M(b) R(Nm). Этим свойством Nm может обладать только в том случае, когда dj {Ф(dj)=H(dj)}.
Другое определение свойства сохранения использует веса позиций Ѡbi.
В этом случае сеть Nm является сохраняющей, если ∑ M(bi)x Ѡbi=const (bi B)
для M(b) R(Nm).
Анализ модели на сохранение важен тогда, когда под динамическими объектами (метками) понимается какие-либо неизменные ресурсы.
Задача распознавания принадлежности произвольной сети Петри кассу правильных( живые и безопасные сети называют правильными сетями) как, впрочем и ряда других задач анализа сетей Петри, решается путем построения для нее дерева достижимых маркировок, являющегося конечным представлением множества R(S0). Вершинами этого дерева сопоставляются элементы множества R(S0).
Однако множество R(S0) может быть бесконечным. Для того, чтобы получить конечное представление бесконечного множества, в одну и ту же вершину дерева помещают подмножество маркировок. С этой целью для обозначения числа точек в позиции вводят специальный символ Ѡ, который со-
ответствует бесконечно большому числу. Для него справедливы Ѡ+ V= Ѡ ; Ѡ-V=
Ѡ, где V целое число.
