Chast_2_3_l_9-12

106

Выберем начало координат где-либо внутри системы зарядов. ri –

радиус-вектор заряда qi , rM – радиус-вектор точки наблюдения М, rPi M –

расстояние между точкой расположения i-го заряда Pi и точкой наблюдения М.

Мы найдем простое приближенное выражение для потенциала в точке М в случае, если точка М находится далеко от совокупности зарядов, т.е.

rM 3V .

Точное значение потенциала в точке М:

Разложим функцию точки М

в ряд Тейлора в окрестности точки x, y ,z (в силу малости xi, yi, zi по сравнению с x, y, z). Возьмем пока первые два члена разложения:

Тогда:

Величина

зависит от величин зарядов и их места расположения и называется дипольным или электрическим моментом системы зарядов.

107

Если суммарный заряд системы зарядов равен нулю ( qi 0 ), то

i

дипольный момент не зависит от выбора начала координат.

Действительно:

ri ri a ,

где a – постоянный вектор, соединяющий начала координат 0 и 0 (рис. 2.60).

Рис. 2.60. К доказательству независимости дипольного момента электронейтральной системы зарядов от выбора начала координат

Тогда:

p qi ri qi ri a qi ri a qi p .

i i i i

Найдем grad 1 в (2.111): rM

отрицательные заряды системы и их радиус-векторы. Тогда:

109

p q d ,

где d - вектор, соединяющий заряды и направленный от отрицательного заряда к положительному.

Если полный заряд системы равен нулю, то, как следует из (2.113),

потенциал ее поля на больших расстояниях:

Напряженность электрического поля в этом случае равна:

Результирующая напряженность при взятии двух членов разложения, как это следует из (2.113) и (2.115):

Поле, обусловленное первым членом разложения, совпадает с полем точечного заряда, помещенного в начало координат и равного по величине суммарному заряду системы.

так как функция 1 , как и потенциал точечного заряда, расположенного в rM

начале координат, является гармонической функцией во всех точках (кроме начала координат, но точка М не может по условию находиться в начале координат).

Теперь, меняя порядок суммирования, можно записать:

зарядов и их места положения. Эта система чисел называется тензором квадрупольного момента. Обозначим:

Найдем входящую в (2.116) вторую производную:

Следовательно, в силу симметрии тензора D , число независимых

компонент у него равно 6.

Легко заметить, что между компонентами существует связь:

D11 D22 D33 0 .

Следовательно, число независимых компонент равно 5.

В качестве примера рассмотрим систему 4-х зарядов, расположенных в вершинах параллелограмма с чередующимися знаками зарядов (рис. 2.64).

Рис. 2.64. Квадруполь

потенциала первый и второй члены будут равны нулю, а отличным от нуля будет третий член разложения, который определяется тензором квадрупольного момента. Такая система зарядов называется квадруполем.

114

Как всякий симметричный тензор, тензор квадрупольного момента можно привести к главным осям, т.е. существует такая система координат x', y', z', в

которой отличны от нуля только компоненты D , D , D . Штрихи опустим.

11 22 33

Тогда в новой системе координат

D11 1 qi 2xi2 yi2 zi2 D1 ; 3 i

D22 1 qi 2 yi2 xi2 zi2 D2 ; 3 i

D33 D11 D22 D1 D2 D3 .

Следовательно, в системе координат, совпадающей с главными осями,

тензор квадрупольного момента характеризуется двумя независимыми компонентами.

Весьма важным является частный случай осесимметричного распределения зарядов (в системе координат, совпадающей с главными осями):

D3 D1 D2 D .

D называют в этом случае квадрупольным моментом.

Итак, при взятии трех членов разложения потенциал на далеких расстояниях ( rM 3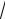V ):