Chast_3_2_l_19-21

204

u dr , dt0

где dt0 - собственное время.

Здесь v – скорость частицы, а не скорость системы О' относительно системы О.

Легко убедиться в том, что

u2 ux2 u2y uz2 u2 c2 .

4-вектор скорости является времениподобным вектором.

4-вектор ускорения:

w du . dt0

Можно показать непосредственным вычислением, что w2 0 .

4-вектор ускорения – пространственно подобный вектор. Имеем u2 c2 .

Продифференцируем по собственному времени

2 u du 2u w 0. dt0

u и w ортогональны между собой в четырехмерном пространстве.

46. Уравнения динамики материальной точки

Закон инерции Ньютона является инвариантным относительно преобразований Лоренца. Если в некоторой инерциальной системе отсчета О частица движется неускоренно, то при переходе к другой инерциальной

205

системе О' движение ее также останется неускоренным. Это следует из формул

преобразования скоростей Эйнштейна.

Для нахождения релятивистски-инвариантной формы уравнений динамики (второго закона Ньютона) их необходимо представить в виде соотношений типа a b , где a и b – четырехмерные векторы.

Инерционные свойства тела или частицы можно охарактеризовать некоторым скаляром – инвариантной массой или массой покоя m0 . Значение массы покоя является константой, характерной для каждого вида элементарных

В предельном случае v << c три пространственные компоненты импульса переходят в обычные компоненты импульса частицы

px m0vx , py m0vy , pz m0vz .

Естественным релятивистским обобщением уравнений динамики Ньютона являются уравнения

где F – некоторый четырехмерный вектор, называемый четырехмерной силой или силой Минковского.

Эти уравнения будем называть уравнениями релятивистской динамики.

В компонентах

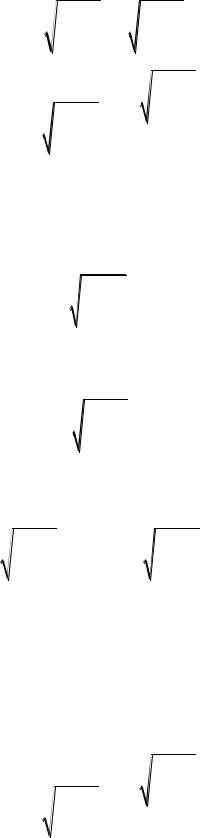
207

Последнее подчеркнутое равенство через компоненты:

Fxux Fyuy Fzuz F u 0 .

Подставим выражение для F через F:

F v – есть работа силы, производимой над частицей в единицу времени.

Следовательно, в левой части есть изменение энергии частицы в единицу времени.

Полная энергия частицы

m v , именуемую релятивистской массой или просто массой и определяемую как коэффициент пропорциональности между p и v

208

Релятивистская масса зависит от скорости и поэтому является функцией не только свойств частицы, но и состояния ее движения. Масса m v не является релятивистски-инвариантной величиной. Масса, измеренная приборами, находящимися в различных инерциальных системах отсчета,

движущихся друг относительно друга, будет различной.

Из выражения для полной энергии и для компонент импульса следует:

p i Ec .

С помощью этого соотношения импульс и энергия оказываются объединенными в один 4-вектор, который можно назвать 4-вектором энергии и импульса

Компоненты 4-вектора энергии и импульса не являются релятивистски-

инвариантными. Как трехмерный импульс, так и энергия являются относительными величинами. Они преобразуются так:

Эти соотношения показывают, что при преобразованиях Лоренца энергия и компоненты импульса выражаются друг через друга.

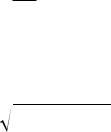
209

Инвариантной величиной является не энергия и импульс порознь, а как всегда квадрат 4-вектора, т.е. величина

Подставляя выражения для px , py и pz , получим:

Таким образом, 4-вектор энергии и импульса является времениподобным вектором.

Предыдущее выражение можно записать в виде

p2 E2 m2 c2 .

c2 0

Отсюда получаем следующую связь между энергией и трехмерным импульсом

E 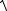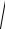p2c2 m02 c4 .

Отсюда, если масса покоя частицы m0 0 (например, фотон), то

E pc .

Обратимся к энергии. Если скорость частицы равна нулю, то ее полная

Отсюда

210

Отсюда при v << c

Eкин m0v2 . 2

При записи выражения для энергии частицы (3.24) можно было записать более общее выражение

Константу, на первый взгляд, необходимо было бы выбрать из соображений, что при v = 0 (здесь v – скорость движения частицы) энергия частицы должна быть равна нулю. Тогда константа получилась бы равной

m0c2 . Однако, константа была взята равной нулю. При этом приняты

следующие соображения: формулы преобразования для импульса должны переходить в формулы преобразования скоростей Галилея при u << c (u –

скорость движения частицы) и v << c (v – скорость движения системы О'

относительно системы О).

Имеем:

(Здесь v – скорость движения системы О' относительно системы О).

Если E m0c2 при u << c, то при v << c получим:

211

pp m v .

xx 0

Отсюда

uu v .

xx

Если бы константа в выражении для энергии была принята равной

Эту формулу называют формулой Эйнштейна или законом эквивалентности массы и энергии.

Если силы на частицу не действуют, то из формулы dEdt F v

следует, что Е = const (закон сохранения энергии).

Если силы на частицу не действуют, то из закона динамики материальной точки (3.22) следует, что p const (закон сохранения импульса).

Из формулы Эйнштейна следует закон сохранения релятивистской массы m v const .

Один закон – закон сохранения энергии или релятивистской массы. Т.е.

из формулы Эйнштейна следует, что одновременно с законом сохранения энергии автоматически имеет место закон сохранения релятивистской массы.

Вопросы и задачи к лекции 19

206-1. Что такое четырехмерный радиус-вектор?

207-2. Дайте определение четырехмерного вектора.

212

208-3. Что такое: 1) пространственно подобный вектор?

2) времениподобный вектор?

209-4. Дайте определение четырехмерного вектора скорости. Запишите выражения для компонент этого вектора.

210-5. Дайте определение четырехмерного вектора ускорения.

211-6. Первые три компоненты четырехмерного вектора скорости равны

2 108 м / с , 1,73 108 м / с и 0 м / с . Найдите четвертую компоненту u .

212-7. Покажите, что четырехмерный вектор скорости и ускорения ортогональны в четырехмерном пространстве.

213-8. Покажите, что закон инерции (первый закон Ньютона) является инвариантным относительно преобразований Лоренца.

214-9. Дайте определение четырехмерного вектора импульса. Запишите выражения для его компонент.

215-10. Запишите уравнения динамики в четырехмерной форме.

216-11. Запишите уравнения динамики для первых трех компонент, а так же в векторном виде.

217-12. Выведите выражение для полной энергии частицы. Объясните,

почему константа в общем выражении для энергии выбрана равной нулю.

218-13. Выведите выражение для кинетической энергии частицы при произвольной скорости движения.

219-14. Что такое четырехмерный вектор энергии и импульса?

220-15. Запишите формулы преобразования компонент трехмерного импульса и энергии при переходе от одной инерциальной системы отсчета к другой.

221-16. Найдите квадрат четырехмерного вектора энергии и импульса.

Времениподобный или пространственно подобный этот вектор?

222-17. Запишите выражение для полной энергии частицы через ее трехмерный импульс. Каково это выражение для энергии в случае, если масса покоя m0 0 .

213

223-18. Запишите формулу Эйнштейна (закон эквивалентности массы и энергии).

224-19. Запишите формулы преобразования массы при переходе от одной инерциальной системы отсчета к другой.

225-20. Выведите закон сохранения энергии и закон сохранения трехмерного импульса.

Лекция 20

47. Электродинамика теории относительности. Релятивистски-

инвариантная формулировка закона сохранения заряда

В основу релятивисткой электродинамики положены предположения об инвариантности и сохранении электрического заряда. Это соблюдается во всех физических процессах.

Закон сохранения заряда в интегральной форме (2.21):

Разделив на объем V, ограниченный замкнутой поверхностью S, и прейдя к пределу при V 0 , получим закон сохранения заряда в дифференциальной форме:

Для придания закону сохранения заряда релятивистко-инвариантной формы, его следует записать в четырехмерной форме.

Для этого необходимо ввести четырехмерный вектор плотности тока .

Введем его так:

Здесь ic .