Chast_1_l_1_2

1

Лекция 1

1. Введение

Курс электродинамики – вторая часть курса теоретической физики после теоретической механики. Он базируется на курсах общей физики и методов математической физики.

Точнее курс можно было бы назвать «макроскопическая электродинамика». В современной научной терминологии понятие макроскопической электродинамики в целом совпадает с классической теорией электромагнитного поля, основы которой заложил Д.К. Максвелл в своем фундаментальном труде «Трактат об электричестве и магнетизме», который вышел в 1873 году. Г. Герц своими опытами в 1887 -1889 гг. экспериментально подтвердил ее, получив предсказанные Максвеллом электромагнитные волны;

он же придал уравнениям Максвелла их современную форму. В теории Максвелла в изящной сжатой форме обобщены основные экспериментальные и теоретические достижения учения об электромагнетизме.

Завершением классической электродинамики явилось открытие материальной природы электромагнитного поля. Основная заслуга этого открытия (1905г.) принадлежит А. Эйнштейну.

По современным представлениям электромагнитное поле – особый вид материи. Оно характеризуется, с одной стороны, непрерывным распределением в пространстве (электромагнитные волны) и, с другой - обнаруживает дискретность структуры (фотоны); оно обладает способностью распространяться в вакууме со скоростью, близкой к 3 108 м / с и оказывает на заряженные частицы силовое воздействие, зависящее от их скорости.

Современные представления об электромагнитном поле возникли в результате длительной эволюции научных знаний о природе электрических,

магнитных и световых явлений.

«Предшественником» электромагнитного поля был механический мировой эфир Гюйгенса - Френеля. Это гипотетическое вещество,

2

всепроникающее и невесомое, на протяжении долгого времени считалось носителем световых явлений. Фарадей ввел в физику электрическое и магнитное поля, рассматривая их как состояния особой среды – электромагнитного эфира. Возникла двойственность эфира (светоносного и электромагнитного), которая затем, во второй половине XIX в., была устранена Максвеллом, создавшим единую теорию электрических, магнитных и оптических явлений, основанную на представлении об электромагнитном поле.

Носителем электромагнитного поля Максвелл считал единый электромагнитный эфир; оптика и электромагнетизм объединились под общим названием «физика эфира».

Опыты определения скорости движения Земли относительно эфира,

проведенные вначале XX в. потерпели полную неудачу. Ее причину объяснила специальная теория относительности, отрицающая существование среды,

относительно которой мыслимо определение абсолютной скорости движения тел.

Эйнштейн совершенно отказался от применения термина «эфир» для обозначения среды – носителя электромагнитных явлений. Этим носителем является само электромагнитное поле, оно материально и обладает всеми свойствами материи – массой, импульсом, энергией, которая способна превращаться в другие виды энергии в строго эквивалентных количествах.

Теория электромагнитного поля полностью сохранила свое значение и в наше время: область ее практических приложений продолжает расширяться.

Она является теоретическим фундаментом электро- и радиотехники,

электроники, ей принадлежит ведущее место в таких дисциплинах как электрохимия, биофизика, астрофизика и др. Знание ее основ обязательно для каждого физика. Физика XX в. (квантовая механика) отнюдь не «отменила» классическую теорию поля, а лишь видоизменила физический смысл ряда понятий и установила границы ее применимости.

Классическая теория поля носит макроскопический характер; иначе говоря, она является феноменологической теорией. Это означает, что в ней не

3

учитывается атомно-молекулярная структура вещества, полностью или частично заполняющего пространство, в котором имеется поле. Наличие вещества учитывается путем введения ряда коэффициентов (диэлектрической

и магнитной проницаемостей, удельной проводимости ), которые часто полагают для каждого однородного вещества постоянными величинами, не зависящими от особенностей поля (его напряженности и частоты). В этой формальной теории вакуум отличается от вещества, если оно заполняет все пространство, лишь другими значениями указанных выше коэффициентов. Не учитывается и атомистическая структура зарядов (их дискретность).

Учет строения вещества привел к возникновению классической электронной теории или классической микроскопической электродинамики,

основателем которой стал Г. Лоренц. Несмотря на возникновение квантовой физики, классическая электронная теория не утратила своего значения до сих пор.

Лоренц предложил исключительно удачный и плодотворный метод усреднения истинных микроскопических значений физических величин и получения их макроскопических значений, которые используются в

макроскопической физике и технике.

Лоренц ввел понятия физически бесконечно малых объемов,

поверхностей, отрезков, отличающиеся от определений аналогичных величин в

математике. Так, по Лоренцу физически бесконечно малый объем

(ф.б.м. объем):

1) должен быть очень большим по сравнению с микроскопическими неоднородностями вещества, обусловленными его атомно-молекулярным строением. Поскольку линейные размеры атомов имеют порядок 10 8 см,

линейные размеры l ф.б.м. объема должны удовлетворять неравенству:

l10 8 см;

2)должен быть весьма малым по сравнению с макроскопическими неоднородностями вещества (дефекты изделий, какими являются раковины,

4

трещины, чужеродные включения и т.п.). Можно, например, потребовать,

чтобы ф.б.м. объем был значительно меньше 10 3 см3 .

Макроскопическим значением физической величины по Лоренцу следует считать её значение, которое получают при усреднении истинных микроскопических значений данной величины по физически бесконечно малому объему (или поверхности или отрезку):

1

макро микро V V микро dV .

Здесь dV – математический бесконечно малый объем, а V – ф.б.м. объем.

Будем пользоваться системой единиц СИ, в которой основными единицами являются метр (м), килограмм (кг), секунда (с) и ампер (А). Первые три единицы известны из курсов общей физики и теоретической механики.

Напомним определение единицы силы тока (ампера): один ампер – это сила такого тока, который при протекании по двум прямолинейным бесконечно длинным параллельным проводникам, расположенным в вакууме на расстоянии 1 м, создает силу взаимодействия между ними равную 2 10 7 Н на один погонный метр.

Предлагаемые Вашему вниманию «Лекции по электродинамики с вопросами и задачами» состоят из 4 частей: основы векторного анализа и математической теории поля, электродинамика поля зарядов и токов в вакууме,

специальная теория относительности и электродинамика поля зарядов и токов в среде (макроскопическая электродинамика).

5

ЧАСТЬ 1. ОСНОВЫ ВЕКТОРНОГО АНАЛИЗА И МАТЕМАТИЧЕСКОЙ

ТЕОРИИ ПОЛЯ

2. Векторы. Проекция вектора на направление и на оси декартовой системы координат. Сложение (вычитание) векторов и умножение на число

Векторы

Вектором называется величина, которая характеризуется модулем и направлением. Модуль – это «длина» вектора в тех единицах, в которых измеряется величина его выражающая. Например, вектор силы F F . Его

модуль F выражается в ньютонах (Н). Пример F 3H . Модуль обозначается тем же символом, но без черты (стрелочки).

При графическом изображении вектора выбирается масштаб. Например, в

1 см 0,5 Н (рис. 1.1).

Рис. 1.1. Графическое изображение вектора

Геометрический аналог вектора F также будем обозначать F ( F 6см )

и слова «геометрический аналог» опускать.

Проекция вектора на направление и на оси декартовой системы координат

Проекцией вектора F на направление n называется величина

Fn F cos (рис. 1.2)

6

Рис. 1.2. Проекция вектора на направление n

Проекции вектора на оси декартовой системы координат будем обозначать Fx , Fy , Fz (рис. 1.3).

Рис. 1.3. Проекции вектора на оси декартовой системы координат

Как видно из рис. 1.3:

Вектор полностью задан, т.е. его модуль и направление, если заданы три его проекции Fx , Fy , Fz . Очевидно,

F Fx ex Fy ey Fz ez

(умножение на число и сложение векторов см. ниже),

F 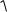Fx2 Fy2 Fz2 .

Если через x1 - обозначить координату начала вектора, а через х2 -

координату конца вектора, то, очевидно, Fx x2 x1. Аналогично Fy y2 y1

и Fz z2 z1.

Сложение (вычитание) векторов и умножение на число

Пусть имеются два вектора

a ax ex ay ey az ez ,

b bx ex by ey bz ez .

Суммой (разностью) этих векторов называется вектор:

a b (ax bx )ex (ay by )ey (az bz )ez .

Произведением вектора a на число u называется вектор

a b xb2 xa1 ex yb2 ya1 ey zb2 za1 ez ,

т.е. сложение производится по правилу, изображенному на рис.1.4: начало вектора b совмещается с концом вектора a , начало суммы a b совпадает с началом вектора a , конец суммы a b совпадает с концом вектора b (или правило параллелограмма (рис. 1.4)).

Рис. 1.4. Графическое сложение векторов

Если при вычитании положить xb1 xa1, yb1 ya1 , zb1 za1, т.е. начала векторов совместить, то

a b xa2 xb2 ex ya2 yb2 ey za2 zb2 ez .

Т.е. разность a b это вектор, имеющий начало в конце вектора b и конец – в

конце вектора a (вектор a b направлен из конца вектора b (вычитаемого) к

концу вектора a (уменьшаемого)) (рис. 1.5).

8

Рис. 1.5. Графическое вычитание векторов и умножение на число

3. Скалярное и векторное произведение векторов. Двойное векторное произведение

Скалярное и векторное произведение векторов

Пусть имеются два вектора a и b (рис.1.6).

Рис. 1.6. К определению скалярного произведения векторов

Перенесем начало вектора b в начало вектора a (или наоборот).

По определению скалярным произведением векторов a и b называется

скалярная величина ab :

где - угол между векторами.

Важные формулы, которые желательно запомнить, будут заключены в прямоугольную рамку.

Через проекции получаем

По определению векторным произведением векторов a и b называется вектор a b , модуль которого равен ab sin , где - угол между векторами

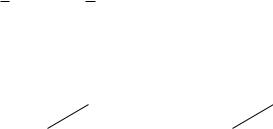
10

Проверим справедливость этой формулы.

ey az by cz bz cy ax bx cy by cx

ez ax bz cx bx cz ay by cz bz cy ,

b ac c ab bx ex by ey bz ez ax cx ay cy az cz

Здесь подчеркнуты одинаковые члены (после умножения на a y , az , bx

иcx ).

4.Скалярное и векторное поля. Градиент скалярного поля

Скалярное и векторное поля

Скалярная функция от координат называется скалярным полем (рис. 1.8):

Рис. 1.8. К определению скалярного и векторного полей