Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет им. Т. Шевченко

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

OFP-Tretyak-Lozovski

.pdf

Скачиваний:

Добавлен:

19.03.2015

Размер:

13.24 Mб

Скачать

☆

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 7222 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ

222

∆l

Рис. 9.7. Виникнення різниці потенціалів	Рис. 9.8. Метод компенсування різниці
через незбіг положення бічних контактів	Рис. 9.8. Метод компенсування різниці
через незбіг положення бічних контактів		потенціалів незбігу
при вимірюванні поля Холла		потенціалів незбігу
при вимірюванні поля Холла
9.5.3. Магніторезистивний ефект

Як ми бачили вище, рух носіїв напівпровідника, що знаходиться під дією магнітного поля, характеризується викривленням їхніх траєкторій, що спричинює зміни складової струму вздовж напрямку електричного поля, прикладеного до напівпровідника. Отже, можна стверджувати про зміну провідності напівпровідника у напрямку Е. Це явище називається магніторезистивним ефектом або ефектом Гаусса, його можна виміряти експериментально. Іноді кажуть, що під дією магнітного поля в напівпровіднику з'являється ефект магнітоопору, появу якого легко зрозуміти із таких простих міркувань. Завдяки дії сили Лоренца поперечне магнітне поле відхиляє носії заряду у напрямку, перпендикулярному дрейфу, що спричиняє ефективну зміну довжини вільного пробігу. Дослідимо на якісному рівні появу ефекту магнітоопору. Для цього розглянемо зміну довжини вільного пробігу носія заряду внаслідок відхилення від напрямку зовнішнього електричного поля (рис. 9.9). Рух електрона між двома перерізами показано штрихованими лініями. Нехай при вимкненому магнітному полі відстань між цими перерізами дорівнює середній довжині вільного пробігу l у напрямку Е. Під дією магнітного поля електрон рухатиметься викривленою траєк-

торією. Якщо це викривлення невелике,	то припустимо, що електрон
рухається вздовж прямої, яка відхи-			l
лена від OB на малий кут φ. Елек трон,			l
що пройшов відстань l, за руху вздовж
траєкторії буде розсіюваний. Це озна-
чає, що ефективна довжина вільного			C
пробігу вздовж напрямку поля Е змен-	О	ϕ	C	B
пробігу вздовж напрямку поля Е змен-	О	ϕ		B
шується на величину ∆l = CB. Оскільки
OA = OB = l, а кут ϕ є малим, з елеме н-
тарної геометричної побудови знахо-			A
димо, що ∆l = l ϕ2. Після підстановки	Рис. 9.9. Зміна довжини вільного
значень кутів Холла електронів і дірок	пробігу носія заряду, спричинена
(за нехтування відмінністю від одиниці	відхиленням від напрямку Е
Холл-фактора), отримуємо	під дією магнітного поля

223	Розділ 9. ЯВИЩА ПЕРЕНЕСЕННЯ В НАПІВПРОВІДНИКАХ

lp				l
	= µ2	B2	та	n = µ2 B2 .	(9.166)
	= µ2	B2	та	n = µ2 B2 .	(9.166)
lp	p			n
lp				ln

Вважаючи, що зміни опору під дією магнітного поля відбуваються за рахунок зміни ефективної рухливості, яка викликана зменшенням ефективної (у напрямку дії електричного поля) довжини вільного пробігу, можна записати оцінку

leff

або µ

= µ − ∆µ, де

∆l

< τ >

eff

∆µ =

eff

Звідси маємо для провідності σeff = σ0 – ∆σ. Після введення параметра

α = ∆σ/σ0 = ∆l/l знайдемо, що для α << 1 ∆R/R = ∆l/l. Далі, використовуючи (9.166), визначимо, що наявність поперечного магнітного поля викликає збільшення електричного опору зразка пропорційно квадрату магнітного поля

∆R µ2 B2				∆Rp			µ2pB2
n	=	n	та			=		.	(9.167)
R		2		R	p		2
n					p

Таким чином, магніторезистивний ефект є ефектом другого порядку за магнітним полем. За простого розгляду ефекту, що привів до формул (9.167), дією холлівського поля знехтовано та прийнято, що всі носії рухаються з однаковою середньою швидкістю і мають однакову середню довжину вільного пробігу. Розглянемо ефект магнітоопору детальніше, базуючись на розв'язку кінетичного рівняння.

За відсутності магнітного поля напрямок густини струму в ізотропному напівпровіднику J збігається з напрямком електричного поля E. Тоді питомий опір (обернена провідність) визначається як

ρ =	1	=	E .	(9.168)
	σ		J

За наявності магнітного поля напрямок вектора щільності струму не збігається з напрямком електричного поля E, тобто до (9.168) ми маємо підставити замість Е його проекцію на вектор струму – E J/J. Отже питомий опір за наявності магнітного поля запишемо як

ρ	=	E J .	(9.169)
B		J 2

Як ми бачили раніше, у слабкому магнітному полі в лінійному наближенні за B густина струму має вигляд (див. (9.145))

J= e(nµn + pµp )E −rne(pµ2p −nµn2 )(B×E).

Зіншого боку, питомі електронна та діркова провідності визначаються як σn = enµn та σp = enµp, відповідно. Тоді для густини струму можна

записати

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ

224

J = σE −Rσ2(B×E).

(9.170)

Зважаючи на те, що E (B × E) = 0, у лінійному за магнітним полем наближенні отримуємо J2 = (σE)2 і E J = σE2 . Таким чином,

ρ	B	=	1	= ρ,	(9.171)
	B		σ

тобто, як ми це вже отримали з елементарних міркувань, у слабкому магнітному полі магніторезистивний ефект не є ефектом першого порядку. Для визначення цього ефекту необхідно врахувати доданки, квадратичні за магнітним полем. Для однорідного напівпровідника

( EF

= 0)

за

відсутності

градієнта

температури

слабкому полі

(eτ B/m* <<1) вектор χ

, що визначає збурену частину функції розп о-

ділу електронів, має вигляд

(B×E)

e τ

E + eτe

eτe

(B E)B

χn = −

(9.172)

eτ

1+ m*e B

Цю формулу можна спростити

eτe

−1

eτe

≈1

−

Отримаємо

e τ

eτ

−

E +

(B×E)+

(B E)B 1

−

= −

e τe

eτe

(B×E)

eτe

E)B −B

E + m*

+ m*

Оскільки в останньому доданку в дужках стоїть подвійний векторний добуток, запишемо остаточно

			e τ	eτ	eτ		2
							(B×(B×E
χ	n	−	e E +	e (B×E)+		e

			m*	m*		m*
			n	n		n

)) . (9.173)

Якщо обмежитися випадком напівпровідника n-типу із простою зонною структурою, то для густини струму можна записати

225	Розділ 9. ЯВИЩА ПЕРЕНЕСЕННЯ В НАПІВПРОВІДНИКАХ

J = −	e2 2	∫dk	∂f
			∂E0
	4π3(m* )2		∂E0
	n	Ω

τek E

	2		2	3
+ eτ*e	k (B×E)+	e	τe		k [B×(B×E)] k . (9.174)
+ eτ*e	k (B×E)+		* 2		k [B×(B×E)] k . (9.174)
mn		(mn )

У цій формулі наявні інтеграли трьох типів, які можна звести до обчислення інтегралів типу (див. вивід формули (9.84))

jτ = ∞∫k4dkτme	∂f0	, m =1, 2, 3.	(9.175)
	∂E
0

Дійсно, із погляду векторної структури (9.174) та з урахування виведення (9.81), видно, що інтеграл складається з інтегралів типу


			j = ∫dk F(E )k(k Q) =						4π	Q∫∞ F(E )k4dk .	(9.176)
			j = ∫dk F(E )k(k Q) =						3	Q∫∞ F(E )k4dk .	(9.176)
				Ω				0
Оскільки	∂f0		n		e	−E/kBT , то (9.175) можна записати у вигляді
	∂E	= −kBTNc			e			∞
							n	∞
						jτ = −	n	k4dkτme e−E/kBT .			(9.177)
						jτ = −	kBTNc	k4dkτme e−E/kBT .			(9.177)
							kBTNc	∫0

Перейдемо до нової змінної t = E/kBT і як завжди припустимо, що закон дисперсії є квадратичним: t = ( k)2/2mn*kBT , kdk = (mn*kBT/ 2 )dt ,

k = (2mn*kBT/ 2 )1/2t1/2 . Таким чином, маємо

5/2

3/2

∞

jτ

= −

n(2mn )

(kBT )

∫τme e−tt3/2dt .

Введемо позначення

∞

τme e−tt3/2dt ,

< τme

∫0

(9.178)

та із (9.5.58) отримаємо

J = enµ

< τ2

(B×E)+µ2

< τ3 >

(9.179)

E +µ

< τ >3

×(B×E)] .

n < τ >2

J, B, B×J є набором некомпланарних векторів. Для визначення поля E розкладемо його за цим набором

E =a1J +a2B +a3(B×J)

(9.180)

і підставимо розкладання до (9.179), залишаючи доданки порядку не вище, як В2

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ

226

J = enµ				+a	B+a	B×J+µ		< τ2 >		a B×J	+
		a J
	n		1	2	3		n < τ >2			1
+µ	< τ2 >		a	B×(B×J)		+µ2	< τ3	>
									a B×(B×J) .
n < τ >2			3			n < τ >3 1

Розкриваючи подвійні векторні добутки, дорівняємо коефіцієнти при векторах J, B, B×J. Маємо такі рівняння для коефіцієнтів аi:

< τ2 >

< τ3 >

B2a1 ,

1 = enµna1 −enµn2 < τ >2

B2a3

−enµn3

< τ >3

enµ a

+enµ2

< τ2 >

(B J)a

+enµ3

< τ3

(B J)a = 0 ,

n < τ >2

n < τ >3

(B J):

+µ

< τ2 >

a = 0 .

< τ >2

Звідси отримуємо

[1+µ2 B

(9.181)

enµ

= −

µn T (B J),

(9.182)

−

< τ2 >

(1+µ2 B2T

(9.183)

en < τ >2

де

< τ3 >< τ > − < τ 2 >

(9.184)

< τ >4

Після підстановки цих виразів до (9.180) знаходимо

1 < τ2 >

E =

+µ

B T

)−

n T (1

+µ

B T

)(B J)B

−

+µ

B T )(B×J) . (9.185)

enµ

en < τ >2

Скалярно домножимо це рівняння на J і поділімо на J2. При цьому пам'ятаємо, що E J/J2 = ρB, а при B = 0 маємо питомий опір напівпровідника ρ = E/J =1/enµn . Тоді відносна зміна питомого опору напівп-

ровідника в магнітному полі

ρB −ρ	2 2	2	(J B)2
ρ	= µnB TM −µnTM		J 2 .	(9.186)

227	Розділ 9. ЯВИЩА ПЕРЕНЕСЕННЯ В НАПІВПРОВІДНИКАХ

Якщо ϕ – кут між векторами густини струму та магнітного поля, то із цього рівняння можна записати

ρB −ρ = µ2 B2T sin2ϕ,			(9.187)
ρ	n	M
ρ

Таким чином, для напівпровідника n-(p-)-типу зі сферичними ізоенергетичними поверхнями в слабких полях поперечний магнітоопір (ϕ = π/2) пропорційний квадрату магнітного поля та рухливості. Повздовжній магнітоопір (ϕ = 0) у цьому випадку є нульовим. При цьому у випадку, коли час релаксації не залежить від енергії, коефіцієнт ТМ дорівнює нулю. У результаті ефект магнітоопору не спостерігатиметься.

Формулу, аналогічну (9.187), можна отримати й у загальнішому випадку, коли напівпровідник має носії обох знаків. Тоді до (9.179) необхідно додати рівняння діркової складової густини струму

< τ3 >

= enµ

E −r µ

(B×E)+

γµ

[B×(B×E)]

, де γ =

< τ >3

Повний струм можна записати у вигляді

	2			2	3			3
	nµn		− pµp		nµn		+ pµp
J = σ E +rH nµ + pµ					(B×E)+ γ nµ + pµ				[B×(B×E)] .	(9.188)
		n		p		n		p

І, як результат, маємо для напівпровідника із простою зонною структурою, що характеризується двома типами носіїв,

ρ −ρ

(nµn2 − pµ2p )2

r (nµ3

+ pµ3

)− γ

B2sin2ϕ.

(9.189)

(nµ2

+ pµ

)

Видно, що основні висновки про магнітоопір зберігаються і в цьому, загальнішому випадку. Але є одна особливість: на відміну від напівпровідника, де електричний струм забезпечується носіями одного типу, у власного або компенсованого напівпровідника магніторезистивний ефект виявляється й у випадку, коли час релаксації не залежить від енергії. Дійсно, як видно із (9.189), при rH = 1 та γ = 1 величина ∆ρ/ρ ≠ 0. Структура виразу (9.189) свідчить, що перший доданок у квадратних дужках правої частини визначає магнітоопір, обумовлений "закручуванням" траєкторій рухомих носіїв магнітним полем, а другий – описує компенсуючу дію поля Холла, що виникає завдяки обмеженості зразка вздовж вісі OY. Цей факт дозволяє дійти висновку, що явище магнітоопору сильно залежить від конфігурації зразка, оскільки поперечне поле Холла, яке виникає під дією магнітного поля, заважає змінам траєкторії носіїв і зменшує ефект магнітоопору. Дійсно, із (9.189) ми бачимо, що ∆ρ/ρ досягає максимального значення, коли другий доданок

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ

228

у дужках дорівнює нулю. А це означає, що стала Холла

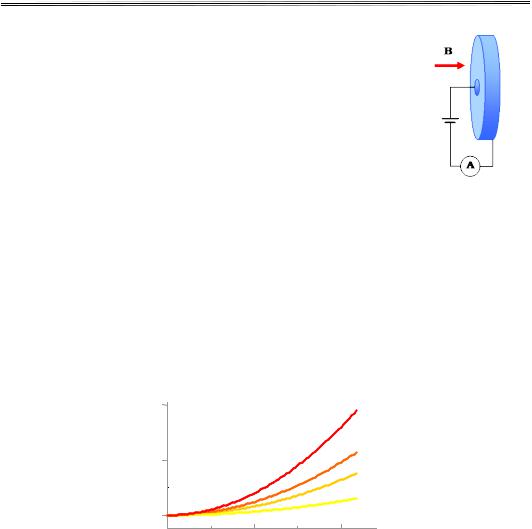
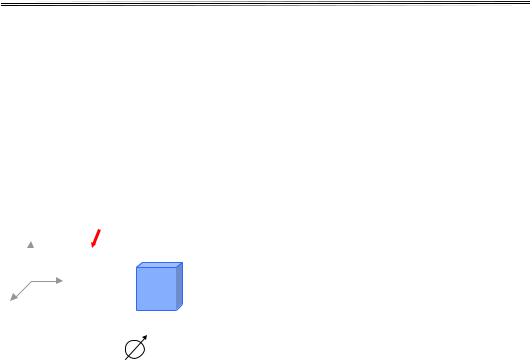
R = 0, тобто для мінімального впливу ефекту Холла (R = 0) варто використовувати зразки, де поле Холла є нульовим. Таким зразком є диск Корбіно (pис. 9.10), де один контакт розташований уздовж зовнішнього, а другий – уздовж внутрішнього кола отвору всередині зразка. Таким чином можна стверджувати, що короткі широкі зразки з омічними контактами на довгих боках, що шунтують ЕРС Холла, дозволяють вимірювати помітніші відносні зміни магнітоопору.

Рис. 9.10. Диск

Корбіно

На рис. 9.11 подано залежність відносного магнітоопору від величини магнітного поля для зразків різної форми. Вище було розглянуто найпростіший випадок сферично симетричного напівпровідника. У напівпровідниках, що не мають сферично симетричної електронної структури, зміна опору в магнітному полі залежить від орієнтації вектора магнітного поля щодо кристалічних осей і може існувати повздовжній магніторезистивний ефект. Вимірюючи величину ∆ρ/ρ за різних орієнтацій магнітного поля щодо осей зразка, можна отримати відомості про параметри зонної структури.

RB/R0

0		B, (T)
0,0	0,4	0,8

Рис. 9.11. Залежність опору зразків різної форми від магнітного поля.

Цифрами позначено зразки з відношеннями довжини до ширини:

1 – 3; 2 – 1; 3 – 1/4; 4 – диск Корбіно

9.5.4. Ефекти Еттінгсгаузена та Нернста

При вимірюванні ефекту Холла іноді виникає додаткове поперечне поле за рахунок різниці температур на бічних гранях зразка. Фізична природа цього явища полягає в тому, що сила Лоренца, яка діє на електрон у магнітному полі, пропорційна його швидкості. Це означає, що електрони із більшими швидкостями відхиляються магнітним по-

229	Розділ 9. ЯВИЩА ПЕРЕНЕСЕННЯ В НАПІВПРОВІДНИКАХ

лем сильніше. Тому бік зразка, в який відхилено більше електронів із великими швидкостями, сильніше нагріватиметься (тут відносно більше швидких частинок, тобто більша температура). Ефект виникнення градієнта температури на бічних гранях зразка в магнітному полі при протіканні через нього струму називається ефектом Еттінгсгаузена. У поданій на pис. 9.12 геометрії величина градієнта температури визначається формулою

∂T

= PE jxBz .

(9.190)

∂y

Коефіцієнт Еттингсгаузена PE

вимірюється в см3К∙Вт–1с–1. Для на-

півпровідника n-типу обчислення цього коефіцієнта дає

= µn

< Eτn2 > −

< τn2 >< Eτn

> , (9.191

eκ

< τ >2

< τ >3

де κ – теплопровідність зразка. Видно, що

коефіцієнт

Еттингсгаузена

дорівнює

нулю, якщо час релаксації не залежить

від енергії. Різниця температур на бічних

гранях зразка призводить до виникнення

Рис. 9.12. Схема вимірювання

термоелектричної різниці потенціалів на

ефекту Еттингсгаузена.

контактах метал–напівпровідник, що

У поданій геометрії верхня грань

додається до різниці потенціалів, обумо-

зразка охолоджується, а нижня –

вленої ефектом Холла. Для зразка з л

і-

нагрівається, тобто Т1>Т2

нійними розмірами

1×10–1×10–2 см3,

що

знаходиться в магнітному полі Bz = 0,1T, через який проходить струм

10–3 А, коефіцієнт Еттингсгаузена РЕ = 60 см3К∙Вт1с–1. Різниця потенціалів, що визначається ефектом Еттингсгаузена VЕ, при цьому становить

3∙10–9 B. Оскільки відношення VE/VH 10−5 (де VH – е.р.с. Холла), то за-

звичай внеском цього ефекту можна знехтувати.

Ще одним гальваномагнітним ефектом є ефект Нернста: у зразку, до якого прикладене магнітне поле, перпендикулярне до напрямку електричного, виникає повздовжня різниця температури. Виникнення градієнта температури, паралельного електричному полю, пояснюється тим, що більша сила Лоренца діє на швидкіші електрони, унаслідок чого вони відокремлюються геометрично від повільних, на які діє менша сила Лоренца. У результаті вздовж грані, на яку вони відх и- лятимуться, виникне градієнт температури. Ефект Нерста є прикладом повздовжнього гальваномагнітного ефекту.

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ

230

9.6. Термомагнітні ефекти

Термомагнітними ефектами називається група явищ, що пов'язані із впливом магнітного поля на електричні та теплові властивості напівпровідників, в яких утворено градієнт температури. Термомагнітні явища, як і гальваномагнітні, обумовлені викривленням траєкторії носіїв заряду в магнітному полі. Іншими словами, магнітне поле викривлює електричний струм (що протікає зразком), спричинений перенесенням заряджених частинок потоком теплоти. У результаті з'являється складова електричного струму і теплового потоку, перпендикулярна магнітному полю. При цьому можуть змінюватись електронні властивості зразка вздовж градієнта температур.

До термомагнітних явищ належать повздовжній і поперечний ефекти Нернста–Еттингсгаузена та повздовжній і поперечний ефекти Риги–Ледюка. Оскільки термомагнітні ефекти не мають такого широкого застосування, як гальваномагнітні ефекти Холла та магнітоопору, зупинимось коротко на формулюванні деяких експериментальних аспектів їх визначення. Зрозуміло, що всі термомагнітні явища можна послідовно розглянути в рамках розв'язку кінетичного рівняння, і коефіцієнти Нернста–Еттингсгаузена та Риги–Ледюка – обчислити в термінах середніх часів релаксації. Найпростіше можна виміряти поперечний ефект Нернста–Еттингсгаузена, який полягає в тому, що наявність градієнта температури вздовж вісі OX зразка, що є причиною теплового потоку вздовж цієї вісі, приводить до появи в магнітному полі на поперечних гранях зразка різниці потенціалів. Його фізична природа викликана тим, що потік тепла в напрямку вісі OX викликає результуючий струм швидких електронів від гарячого кінця зразка до холодного. Оскільки відхилення електронів у магнітному полі пропорційне їхній швидкості, то як результат у напрямку OY виникають одночасно і поперечна ЕРС, і поперечний градієнт температури. Для вимірювання ефекту Нернста використовують схе-


					му, аналогічну до тієї, що заст о-
	y				совується при вимірюванні ефе-
			–		кту Холла (pис. 9.13). Якщо в цьому


		T1	T2	VN	експерименті		на	поперечних
		x	+	VN	гранях зразка підтримувати різні
		x			гранях зразка підтримувати різні
z					температури й		тим самим ство-
		В			температури й		тим самим ство-
					рювати	градієнт		температури
					рювати	градієнт		температури
					∂T/∂x, то вздовж зразка протіка-
	Рис. 9.13. Схема вимірювання ефекту				∂T/∂x, то вздовж зразка протіка-
	Рис. 9.13. Схема вимірювання ефекту				тиме потік тепла, а між верхньою
		Нернста–Еттингсгаузена.			та нижньою гранями виникне рі-
При Т1>Т2 у представленій геометрії для					та нижньою гранями виникне рі-
При Т1>Т2 у представленій геометрії для					зниця	потенціалів		Vy. Напруже-
		зразка n-типу коефіцієнт			зниця	потенціалів		Vy. Напруже-

231	Розділ 9. ЯВИЩА ПЕРЕНЕСЕННЯ В НАПІВПРОВІДНИКАХ
Нернста–Еттингсгаузена є позитивним		ність поля Нернста при цьому ви-
		значається формулою
	E	=Q		∂T	B		.	(9.192)
	y		N ∂x			z

Коефіцієнт Нернста QN (вимірюється в см2с–1К–1) вважається позитив-

ним, якщо вектори T, E, B утворюють праву трійку векторів. Він виражається через середні часи релаксації і для напівпровідника n-типу

QN =	µ	< Eτ2 >	−	< τ2 <> τE >
QN =	T	< τ >2	−	< τ >3	n	.
	n	n		e	n
		n		n

Тут і нижче використовуватимемо таке позначення

	p	m		4		∞	p	m		−t	3/2
< E		τ >					t =		e		t dtτ .
< E		τ >					t =		e		t dtτ .
		e	3		π ∫0			e
			3		π ∫0

(9.193)

(9.194)

Як видно з цієї формули, у випадку,коли час релаксації не залежить від енергії, QN = 0. Для зразка з лінійними розмірами 1×10–1×10–2 см3, що знаходиться в магнітному полі Bz = 0,1T, і градієнтом температури 10 K cм–1 коефіцієнт Нернста–Еттингсгаузена QN 10−1м2c−1K−1 . Часто цей

ефект називають тепловим аналогом ефекту Холла (див., напр. [1]). Але ця аналогія не зовсім повна, оскільки за незалежного від енергії часу релаксації поперечний ефект Нернста–Еттингсгаузена відсутній (див.


(9.193)), у той час, як при τ(Е) = const				ефект Холла спостерігається.
Якщо в геометрії експерименту				y				Ty 2
(рис. 9.14) нагрівати зразок так, щоб							В

у напрямку OX утворювався гра-
дієнт температури, то за ненульо-					x	Тx1		Tx2

вого	магнітного поля		виникне	z
градієнт		температури	також					Ty 1
вздовж вісі OY. Таке явище нази-
вається ефектом Риги–Ледюка,				Рис. 9.14. Схема вимірювання ефекту
виникнення якого можна пояс-						Риги–Ледюка.
нити: оскільки відхилення елект-				У представленій геометрії за рахунок
ронів у магнітному полі пропор-				наявності градієнта температури вздовж
ційне	їхнім швидкостям, то за			вісі OX (Тх1		>Тх2) верхня грань зразка
наявності		градієнта температури		охолоджується, а нижня – нагрівається
						(Ту1>Ту2)
вздовж вісі ОХ швидкіші електро-

ни, що знаходяться біля гарячої грані зразка, відхиляються дужче в напрямку OY. Це приводить до концентрації на нижній грані зразка швидкіших електронів, отже температура цієї грані буде більшою за температуру верхньої. Іншими словами, ефект Риги–Ледюка є темпера-

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 7222 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.11.2019317.44 Кб1OE_Lab_1.doc
#
08.11.2019176.13 Кб4OE_Lab_3.doc
#
08.11.2019301.57 Кб6OE_Lab_5.doc
#
08.11.2019360.45 Кб1OE_Lab_6.doc
#
08.11.2019218.62 Кб2OE_Lab_7.doc
#
19.03.201513.24 Mб64OFP-Tretyak-Lozovski.pdf
#
19.03.20151.28 Mб17Ohienko_Istoriia_ukr_literat_movy_2001.pdf
#
19.03.20151.61 Mб12Ohorona_pratsi.pdf
#
19.03.2015151.55 Кб201OiV_1-6.docx
#
18.11.201971.68 Кб1olimp_biol_8.doc
#
06.09.2019181.25 Кб1OncoGen.doc