
- •Московский Государственный открытый университет
- •Понятие хозяйственного механизма
- •Базовая модель
- •Общая схема формализации процессов моделирования хозяйственного механизма
- •Лекция 2 Базовая модель в контексте формализованной схемы моделирования хозяйственного механизма
- •Производственные функции. Агрегирование и дезагрегирование
- •Лекция 3 Синергетический эффект
- •Эффективность создания совместного производства (системы)
- •Механизм инноваций
- •Лекция 4 Многокритериальные задачи
- •Поиск эффективных точек
- •Лекция 5
- •Формализация основных понятий Теории Игр.
- •Принцип Оптимальности
- •Принятие решений
- •Принцип Оптимальности
- •2 Фирма
- •1 Фирма
- •Роль информированности. Формализация информированности в виде стратегии
- •Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
- •Формальное определение
- •Информационное расширение игры
- •Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
- •Ситуация равновесия по Нэшу в информационном расширении игры
- •2 Фирма
- •1 Фирма
- •Лекция 7 Иерархические системы управления
- •Обобщенный принцип максимального гарантированного результата (оп мгр)
- •Иерархическая игра (игра Гермейера)
- •Экономическая интерпретация иерархических игр г1, г2и г3
- •Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
- •2.Аналог игры
- •Лекция 9 Динамические модели принятия решений
- •Слабоустойчивые совместные решения по ю. Б. Гермейеру
- •Динамическая модель принятия решений с непрерывным временем
- •Оптимизация процесса контроля (наблюдения)
- •Литература
- •Лекция 10 Управление ису при неточном знании параметров подсистем
Поиск эффективных точек
Пусть U– компактное
множество, аg1,…,gm– непрерывные функции,gi:U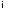 .
.
Теорема (Гермейер).Пустьx0– эффективная точка, причемgi(x0)>0
для всехi=1,…,m.
Тогда существуют положительные числа1,…mтакие, что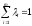 иx0является
точкой максимума функции
иx0является
точкой максимума функции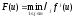 .
.
Доказательство.Положим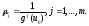 Тогда
Тогда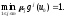
Пусть u– любая точка.
Так как точкаu0– эффективна, найдется номерi,
для которого gi(u)gi(u0),
или, что то же самое,igi(u)1.
Значит,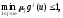 а это означает, чтоu0– одна из точек максимума функции
а это означает, чтоu0– одна из точек максимума функции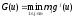 .
.
Остается положить
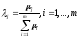 и заметить, что тогдаu0– одна из точек максимума функцииF(u).
Теорема доказана.
и заметить, что тогдаu0– одна из точек максимума функцииF(u).
Теорема доказана.
К сожалению, нельзя утверждать, что
всякая точка максимума функции
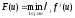 будет эффективной точкой многокритериальной
задачи. ПустьU–
компактное множество, аg1,…,gm– непрерывные функции,gi:U
будет эффективной точкой многокритериальной
задачи. ПустьU–
компактное множество, аg1,…,gm– непрерывные функции,gi:U .
.
Теорема (Гермейер).Пустьu0– эффективная точка, причемgi(u0)>0
для всехi=1,…,m.
Тогда существуют положительные числа1,…mтакие, что иx0является
точкой максимума функции
иx0является
точкой максимума функции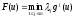 .
.
Доказательство.Положим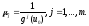 Тогда
Тогда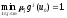
Пусть u– любая точка.
Так как точкаu0– эффективна, найдется номерi,
для которого gi(u)gi(u0),
или, что то же самое,igi(u)1.
Значит,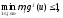 а это означает, чтоu0– одна из точек максимума функции
а это означает, чтоu0– одна из точек максимума функции .
.
Остается положить
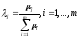 и заметить, что тогдаu0– одна из точек максимума функцииF(u).
Теорема доказана.
и заметить, что тогдаu0– одна из точек максимума функцииF(u).
Теорема доказана.
К сожалению, нельзя утверждать, что
всякая точка максимума функции
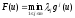 будет эффективной точкой многокритериальной
задачи.
будет эффективной точкой многокритериальной
задачи.
Пример. ПустьU={(u1,u2):
0u11,
0u21},
g1(u)=u1,g2(u)=u2.
При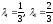 точки максимума функции
точки максимума функции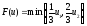 образуют отрезок
{(u1,u2):u1=1, 0.5u21},
но только одна его точка (1,1) является
эффективной.
образуют отрезок
{(u1,u2):u1=1, 0.5u21},
но только одна его точка (1,1) является
эффективной.
Теорема. Пусть существуют такие
положительные числа1,…m, что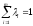 иx0является
точкой максимума функции
иx0является
точкой максимума функции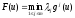 .
Тогда точкаx0является слабо эффективной.
.
Тогда точкаx0является слабо эффективной.
Доказательство.Допустим противное. Тогда найдется такая точкаu1, чтоgi(u1)>gi(u0) для всехi=1,…,m. Но тогдаF(u1)>F(u0), что противоречит условию.
Пусть теперь множество Uвыпукло, а функцииg1,…,gmвогнуты.
Теорема (Карлин). Пустьx0– эффективная точка. Тогда существуют
неотрицательные числаp1,…,p
mтакие,
что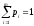 иx0является
точкой максимума функции
иx0является
точкой максимума функции .
.
Доказательство.Не ограничивая
общности, можем считать, чтоgi(u)>0
для всехi=1,…,m.
В силу теоремы Гермейера существуют
положительные числа1,…mдля которыхu0реализует максимум функции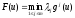 .
.
Тогда (u0,F(u0)) является решением задачи математического программирования
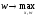 ,
,
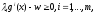
uU,
w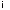 .
.
В силу теоремы Куна–Такера найдутся такие неотрицательные числа i,i=1,…,m, для которых (u0,F(u0)) будет точкой максимума функции
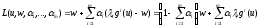
на множестве U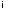 .
Но это возможно, только если
.
Но это возможно, только если
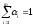 ,
(*)
,
(*)
а тогда u0является
точкой максимума функции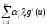 .
.
Остается заметить, что в силу равенства
(*), по крайней мере, одно iне равно нулю. А тогда мы можем положить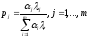 .
.
Теорема.Пусть существуют положительные
числаp1,…,p
mтакие,
что иu0является
точкой максимума функции
иu0является
точкой максимума функции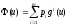 .
Тогда точкаu0является эффективной.
.
Тогда точкаu0является эффективной.
Доказательство.Допустим противное. Тогда найдется такая точкаu1, чтоgi(u1)gi(u0) для всехi=1,…,m, причем, по крайней мере, одно из этих неравенств не обращается в равенство. Умножая эти неравенства наpiи суммируя, получим неравенство(u1)>(u0), что противоречит условию.
Нельзя утверждать, что всякая эффективная
точка может быть найдена в результате
максимизации функции
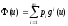 с положительными коэффициентамиp1,…,p
m.
с положительными коэффициентамиp1,…,p
m.
Пример.Пусть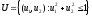 ,g1(u)=u1,g2(u)=u2.Максимум
функции
,g1(u)=u1,g2(u)=u2.Максимум
функции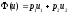 достигается в точке
достигается в точке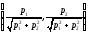 .
В то же время, точка (1,0) является
эффективной.
.
В то же время, точка (1,0) является
эффективной.
С другой стороны, при неотрицательных
коэффициентах p1,…,pm,
точка максимума функции может быть неэффективной в многокритериальной
задаче.
может быть неэффективной в многокритериальной
задаче.
Пример.ПустьU={(u1,u2): 0u11, 0u21}, g1(u)=u1,g2(u)=u2. Точки максимума функции(u)=1g1(u)+0g2(u) образуют отрезок {(u1,u2):u1=1, 0u21}, а эффективной является только одна точка (1,1) этого отрезка.
Теорема.Пусть существуют
неотрицательные числаp1,…,p
mтакие,
что иu0является
точкой максимума функции
иu0является
точкой максимума функции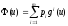 .
Тогда точкаu0является слабо эффективной.
.
Тогда точкаu0является слабо эффективной.
Доказательство.Допустим противное. Тогда найдется такая точкаu1, чтоgi(u1)>gi(u0) для всехi=1,…,m. Умножая эти неравенства наpiи суммируя, получим неравенство(u1)>(u0), что противоречит условию.
Пример
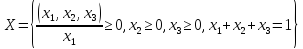
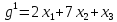

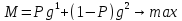
Подставим
крайние точки единичного треугольника
трехмерного пространства
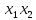
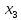
( (0,0,1) (0,1,0),(1,0,0) ) в систему уравнений
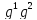 , затем полученные значения
, затем полученные значения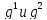 подставим в М и получим 3 прямы
подставим в М и получим 3 прямы
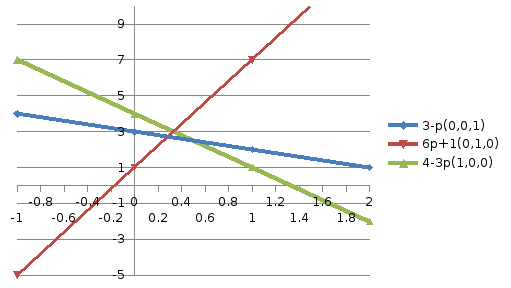
М
Р
Max значение достигается при пересечении прямых 4-3Р и 6р+1, следовательно приравняв их найдет оптимальное значение р
4-3р=6р+1
→ р =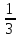 →
→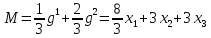
При
(1,0,0) М =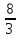
При (0,1,0) М = 3
Значение М в точке (0,1,0) является максимальным и оптимальным по Парето
Примеры
Пример.Пусть множествоUпредставляет собой стандартный симплексU={(u1,u2,u3):u10,u20,u30,u1+u2+u3=1} и имеется два критерияg1(u)=2u1+7u2+u3иg2(u)=3u1+u2+4u3.
Найдем точки максимума функции
(u)=pg1(u)+(1–p)g2(u).
Так как критерии в данной задаче линейны,
а максимум линейной функции непременно
достигается в одной из вершин, то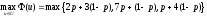 .
Нарисовав графики, нетрудно понять, что
при 0p1/3
максимум достигается в вершине (0,1,0), а
при 1/3p1
он достигается в вершине (0,0,1). Приp=1/3
точки максимума заполняют все ребро,
соединяющие эти вершины. Таким образом,
все точки этого ребра являются
эффективными.
.
Нарисовав графики, нетрудно понять, что
при 0p1/3
максимум достигается в вершине (0,1,0), а
при 1/3p1
он достигается в вершине (0,0,1). Приp=1/3
точки максимума заполняют все ребро,
соединяющие эти вершины. Таким образом,
все точки этого ребра являются
эффективными.
Пример.Пусть множествоUпредставляет собой стандартный симплексU={(u1,u2,u3):u10,u20,u30,u1+u2+u3=1} и имеется два критерияg1(u)=3u1+7u2+u3иg2(u)=4u1+u2+4u3.
Анализ, аналогичный проведенному выше, показывает, что в данном случае эффективными являются все точки, лежащие на двух ребрах: соединяющем вершину (1,0,0) с вершиной (0,1,0) и соединяющем вершины (1,0,0) и (0,0,1). В этом случае множество эффективных точек не выпукло.
В двух предыдущих примерах полезно нарисовать образ множества Uв пространстве критериев.
Пример: дуополия Курно.Две фирмы выпускают однородный товар и продают его на рынке. Цена, складывающаяся на рынке, линейно убывает с ростом суммарного предложения:=a–b(u1+u2), гдеu1иu2объемы выпуска продукции первой и второй фирмой соответственно (по своему смыслу величиныu1иu2неотрицательны). Пусть затраты первой и второй фирм на выпуск единицы продукции равныc1иc2, а их цели состоят в максимизации прибылейg1(u1,u2)=u1–c1u1иg2(u1,u2)=u2–c2u2. Найдем эффективные точки в этой двухкритериальной задаче.
Для этого найдем максимум функции
(u1,u2)=p(u1,u2)+i(1–p)
g2(u1,u2)=u2–c2u2.
Имеем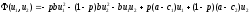 .
При фиксированном управлении одной
фирмы эта функция представляет собой
квадратный трехчлен относительно
управления другой фирмы с отрицательным
старшим коэффициентом. Поэтому, максимум
этой функции достигается в критической
точке тогда и только тогда, когда
последняя лежит внутри областиu10,u20.
В противном случае максимум находится
на границе этой области.
.
При фиксированном управлении одной
фирмы эта функция представляет собой
квадратный трехчлен относительно
управления другой фирмы с отрицательным
старшим коэффициентом. Поэтому, максимум
этой функции достигается в критической
точке тогда и только тогда, когда
последняя лежит внутри областиu10,u20.
В противном случае максимум находится
на границе этой области.
Критическая точка есть решение системы уравнений

Решая эту систему относительно u1иu2, получим параметрическое представление
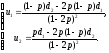
множества эффективных точек.1
Исключив же из этой системы параметр p, получим уравнение
2(u1+u2)2–(d1+2d2)u1–(d2+2d1)u2–d1d2=0
множества эффективных точек. Нетрудно видеть, что это уравнение параболы с осью, являющейся биссектрисой координатных углов. Пересечение этой параболы с неотрицательным квадрантом и дает множество эффективных точек2. Поскольку это множество пересекается с любым лучом, выходящим из начала координат и лежащим в неотрицательном квадранте, других эффективных точек н
Литература
Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.
Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. М.: Наука, 1982.
Карлин С. Математические методы в теории игр, программировании и экономике. М.: Мир, 1964.
