
- •Московский Государственный открытый университет
- •Понятие хозяйственного механизма
- •Базовая модель
- •Общая схема формализации процессов моделирования хозяйственного механизма
- •Лекция 2 Базовая модель в контексте формализованной схемы моделирования хозяйственного механизма
- •Производственные функции. Агрегирование и дезагрегирование
- •Лекция 3 Синергетический эффект
- •Эффективность создания совместного производства (системы)
- •Механизм инноваций
- •Лекция 4 Многокритериальные задачи
- •Поиск эффективных точек
- •Лекция 5
- •Формализация основных понятий Теории Игр.
- •Принцип Оптимальности
- •Принятие решений
- •Принцип Оптимальности
- •2 Фирма
- •1 Фирма
- •Роль информированности. Формализация информированности в виде стратегии
- •Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
- •Формальное определение
- •Информационное расширение игры
- •Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
- •Ситуация равновесия по Нэшу в информационном расширении игры
- •2 Фирма
- •1 Фирма
- •Лекция 7 Иерархические системы управления
- •Обобщенный принцип максимального гарантированного результата (оп мгр)
- •Иерархическая игра (игра Гермейера)
- •Экономическая интерпретация иерархических игр г1, г2и г3
- •Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
- •2.Аналог игры
- •Лекция 9 Динамические модели принятия решений
- •Слабоустойчивые совместные решения по ю. Б. Гермейеру
- •Динамическая модель принятия решений с непрерывным временем
- •Оптимизация процесса контроля (наблюдения)
- •Литература
- •Лекция 10 Управление ису при неточном знании параметров подсистем
Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
Пример
1:
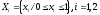
Пусть
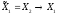 ,
т.е.
,
т.е.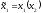 ,
,
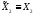 ,
т.е.
,
т.е.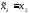
Тогда
(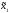 ,
,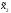 )
)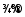
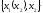 .
.
Фиксируем для примера:
X1=x(x2)=x2^2
X2=x2=1/2.
Тогда эти стратегии проектируются так:
( x 1, x 2 ) ( x 1 (x 2 ) , x 2 ) (x 2/2, ½) =(1/4,1/2)
Пример
2:
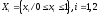
Пусть
x1:
x
2
X
1 т.е.
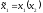 ,
,
x
2 : x
1X
2, т.е.
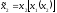 - игрок 2 принимает решение в зависимости
от стратегии первого игрока. Например,
- игрок 2 принимает решение в зависимости
от стратегии первого игрока. Например,
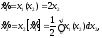
Проектируем:
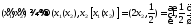 ,
,
так как
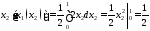 .
.
Полезные свойства стратегий:
На классе стратегий ситуация равновесия по Нэшу существует всегда, необходимо только организовать соответствующий обмен информацией.
На классе стратегий из примера 2 можно сделать равновесной любую взаимовыгодную точку. Взаимовыгодное множество – это множество, где игроки получают больше своих максимально гарантированных результатов, следовательно, паретовскую точку можно сделать равновесной.
Ситуация равновесия по Нэшу в информационном расширении игры
Пусть задана игра:
Г = <
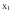 ,
,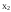 ,
, ,
,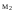 >
>
и ее информационное расширение:
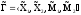

Определение.
(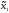 0,
0,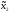 0)-
ситуация равновесия в информационном
расширении игры, еслиM10
=M1(π(
0)-
ситуация равновесия в информационном
расширении игры, еслиM10
=M1(π(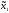 0,
0,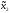 0))=
0))=
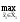 M1(π(
M1(π(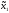 ,
,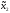 0))
0))
M20=
M2(π(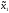 0,
0,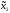 0))=
0))=
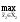 M2(π(
M2(π(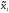 0,
0,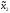 )
)
Заметим ,что
(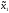 0,
0,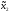 0)
π (х10, х20) –
равновесный исход,но не ситуация
равновесия!
0)
π (х10, х20) –
равновесный исход,но не ситуация
равновесия!
Таким образом, ситуация равновесия может реализоваться на стратегиях
(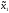 º,
º,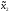 º)
є
º)
є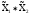
но ее проекция
( хº1, хº2) є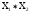
не обязательно равновесная по Нэшу.
Напомним, что стратегия
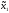 а
= х1а(х2)
называется абсолютно
оптимальной стратегией,
если справедливо равенство:
а
= х1а(х2)
называется абсолютно
оптимальной стратегией,
если справедливо равенство:
M1(x1а(x2),
x2)=
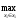 M1(x1,
x2)
M1(x1,
x2)
Определим x2= х2а - оптимальный ответ второго игрока из условия:
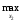 M2(x1а(x2),
x2)
= M2(x1а(x2а),
x2а
)
M2(x1а(x2),
x2)
= M2(x1а(x2а),
x2а
)
Положительные свойства стратегий:
Свойство 1.
Ситуация равновесия всегда существует на классе стратегий
(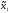 ,
,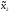 )=(x1(x2),x2)
)=(x1(x2),x2)
Доказательство: Достаточно выбрать
абсолютно оптимальную стратегию
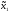 а
= хª1(x2), и
оптимальный ответ на нее
а
= хª1(x2), и
оптимальный ответ на нее а
= х2а
а
= х2а
По определению:
M1(x1а(x2),x2) =
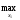 M1(x1,
x2),
M1(x1,
x2),
M2(x1а(x2а),x2а) =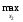 M2(x1а(x2),x2).
M2(x1а(x2),x2).
Тогда, если
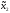 =
х2а, то
=
х2а, то
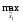 M1(π(
M1(π(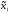 ,x^2а))=
,x^2а))=
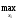 M1(x1(xª2),
xª2)
= M1(x1а(x2а),
x2а
).
M1(x1(xª2),
xª2)
= M1(x1а(x2а),
x2а
).
Если
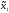 =
=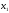 а(
а(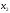 ),
то
),
то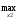 M2(x1а(x2),x2)=
M2(x1а(x2а),x2а), что
соответствует определению ситуации
равновесия в информационном расширении
игры.
M2(x1а(x2),x2)=
M2(x1а(x2а),x2а), что
соответствует определению ситуации
равновесия в информационном расширении
игры.
Свойство 2.
Если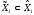 ,
тои
,
тои
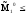
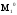
 –
увеличение информации приводит к
возможности увеличения выигрыша.т
–
увеличение информации приводит к
возможности увеличения выигрыша.т
Доказательство:
Первый игрок может не использовать
дополнительную информацию и получить
 .
А если повезёт (дополнительная информация
оказалась полезной), то получит строго
больше.
.
А если повезёт (дополнительная информация
оказалась полезной), то получит строго
больше.
Свойство 3.
Пусть игрок 1 знает х2 .
Определим взаимовыгодное множество для этого случая:
 12={(х1,
х2)
12={(х1,
х2)
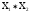 M1(
х1, х2) ≥
M1(
х1, х2) ≥
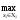 M1(х1, х2);
M1(х1, х2);
M2( х1, х2)
≥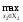
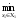 M2(х1,
х2)}.
M2(х1,
х2)}.
Любая точка из этого множества может быть сделана ситуацией равновесия на классе стратегий
{х1(х2), х2[х1(х2)]}
Аналогичное утверждение верно и в симметричном случае, когда игрок 2 знает х1.
Здесь взаимовыгодное множество имеет вид:
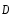 21={(х1,
х2)
21={(х1,
х2)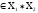 M1(
х1, х2) ≥
M1(
х1, х2) ≥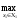
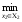 M1(х1,
х2);
M1(х1,
х2);
M2( х1, х2)
≥
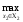 M2(х1,
х2)}.
M2(х1,
х2)}.
А класс использованных стратегий имеет вид:
{ х1 [х2(х1)], х2 (х1)}.
ТРИ игры
Проведем анализ рассмотренных ранее игр,но уже на классе стратегий.
Игра «продавец – покупатель»
В этой игре на классе исходных управлений не существует равновесной ситуации.
Пусть теперь например, покупатель имеет информацию о действиях продавца. Тогда его абсолютно оптимальная стратегия заключается в доверии (без затрат на проверку в случае честного поведения продавца. Оптимальный выбор продавца в этой ситуации –честно взвесить товар. Что приводит к исходу – (честно взвеситл, поверил). Подчеркнем, что эта ситуация не является ситуацией равновесия в исходной игре! Ситуация равновесия реализуется только наклассе стратегий.
Аналогично, если продавец знает выбор покупателя, то его абсолютно оптимальная стравтегия заключается в честном поведении при угрозе проверки ви обмане – в случае доверчивого покупателя. Оптимальный ответ покупателя на эту стратегию – проверять продавца. В этом случае реализуется исход –(честно взвесил, проверил), котороый опять же не является равновесным в исходной игре.
Игра «семейный спор»
В этой игре существуют две неравноценные для партнеров ситуации равновесия: идти вместе на футбол, идти вместе на балет. Эта игра на классе стратегий хорошо иллюстрирует тот факт, что иногда более важно владеть инициативой, а не информацией. Кто из партнеров первым ходит, то есть первым делает выбор и сообщает о нем партнеру, тот и добивается для себя более выгодной ситуации равновесия. Если главенствует муж, то жене придется идти с ним на футбол. Если муж находится «под каблуком», то он обречен ходить на балет.
Заметим. Что в дружной семье главенствующий всегда идет на компромисс, предлагая поочередно наслаждаться балетом и футболом. Однако в этой ситуации мы вывходим за рамки статической модели, определяя интегральный (осредненный по времени) выигрыш вв динамической модели повторящейся игры.
Игра «реклама»
В этой игре существует единственная ситуация равновесия – обоим партнерам рекламировать свой товар. Однако существует более эффективный для обоих партнеров вариант, оптимальный по Парето, - не тратиться на рекламу. Но эта ситуация не является равновесной на классе исходных управлений. Однако эта ситуация принадлежит взаимовыгодному множеству, а значит ее можно сделать результатом проекции равновесных стратегий, включающих в себя договорные обязательства со штрафами за отклонение от них.
Пример. [1]
Пусть биматричная игра имеет вид:
М1= M2=
M2=
Исследуем множество равновесных ситуаций в этой игре.
Имеем для игрока 1:
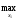
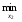 M1(x1,x2) = 0
M1(x1,x2) = 0
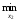
 M1(x1,x2) = 3
M1(x1,x2) = 3
Определим: х2 = х2H- стратегия наказания первого игрока
вторым, из условия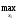
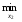 M1(х1,
х2) =
M1(х1,
х2) =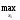 M1(х1,
х2H) В данном
случае имеем х2H=
M1(х1,
х2H) В данном
случае имеем х2H=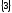 .
.
Далее для игрока 2 имеем:

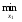 M2(x1,x2)
= 0
M2(x1,x2)
= 0
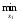
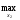 M2(x1,x2) = 3
M2(x1,x2) = 3
Определим х1H (х2) - стратегию наказания второго игрока первым.
2, если х1 = 1
х1H (х2)= 1, если х2 = 2
3 (2), если х3 =3
Сначала найдем равновесные ситуации в исходной игре.
Для этого определим:
x1a(x2) –абсолютно оптимальную стратегию первого игрока и
х2 =x2a– оптимальный ответ второго.
Напомним, что:
x1a(x2):
M1(x1a(x2),
x2) =
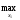 M1(x1,
x2)x2a:
M1(x1,
x2)x2a:
M2(x1a(x2а),
x2a)
=
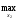 M2(x1a(x2а),
x2).
M2(x1a(x2а),
x2).
Итак:
3, если x2
= 1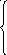
x1a(x2) = 2, еслиx2 = 2
2, если x2
= 3
Аналогично: 3, если x1 = 1
x2a(x1) = 2, еслиx1 = 2
2, если x1 = 3
Единственная ситуация равновесия в исходной игре определяется из условия
x1a(x2а)
=x2a(x1a)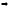 (2,2).
(2,2).
В этой ситуации выигрыши игроков равны (4,4).
Замечание.
Прием построения абсолютно оптимальных стратегий и нахождения их пересечений для определения ситуаций равновесия носит общий характер.
Построим П-множество Парето на классе исходных управлений.
Напомним, что
(x1п,x2п) П
П
если не существует (x1',x2')єХ1*Х2, такой что:
Mi(x1',x2') ≥Mi(x1п,x2п),i=1, 2 (дизъюнкция)
Mi(x1',x2') >Mi(x1п,x2п),i=1 либоi=2 (конъюнкция)
В пространстве выигрышей множество возможных решений имеет вид:
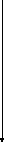
M2
П
7
6
П
4
(4, 4) с.р.

3
2
П



0 2 3 4 6 7 M1
рис.1
Как видно из рис.1:
П = {( 1,1); (1,3); (3,1)},
С выигрышами игроков соответственно
МП = {(6,6); (2,7); (7,2)}.
Непосредственной проверкой убеждаемся, что ни одна из этих точек не является ситуацией равновесия в исходной игре.
Покажем, что эти ситуации могут быть результатом проекции равновесных стратегий вида:
{ х1(х2), х2[х1(х2)]}, {х1[х2(х1)], х2(х1)}.
Покажем, что равновесные стратегии можно выбрать на классе стратегий {x1(x2),x2 [x1(x2)]} .Действительно , пусть
x10
(x2)
= 1, х2=1
 0
= х20
[х1(х2)]
= 1,
0
= х20
[х1(х2)]
= 1,
 =
=
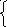
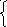
х1н
(х2),
х2 1
, х2н
= 3,
1
, х2н
= 3,
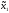

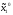
Очевидно, эти стратегии проектируются в точку (х1 = 1, х2=1). В этой точкеM1 = 6,M2 = 6.
Если от этих стратегий отклонится игрок
1, то есть


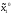 ,
то он получит не больше, чем
,
то он получит не больше, чем
 M1(π(
M1(π(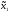 ,
,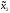 0))=
0))=
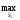 M1(π (
M1(π (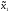 ,
3) =M1(2, 3) = 3 < 6.
,
3) =M1(2, 3) = 3 < 6.
Таким образом, игроку 1 не выгодно
отклоняться от точки (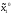 ,
,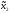 0).
0).
Если же при
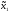 =
=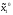 ,
игрок 2 выберет
,
игрок 2 выберет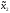

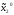 ,
то его выигрыш оценивается величиной
,
то его выигрыш оценивается величиной
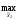 M2[π(
M2[π(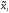 0,
0,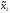 )].
)].
Если
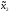 т.ч.
х2
т.ч.
х2 1,
при
1,
при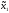 =
=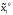 ,
то
,
то
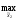 M2[π(
M2[π(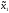 0,
0,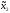 )]
=
)]
=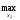 M2(х1H(х2),
х2) = 0 < 6
M2(х1H(х2),
х2) = 0 < 6
Итак, игроку 2 также не выгодно отклоняться
от точки (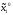 ,
,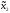 0),
то есть (
0),
то есть ( ,
,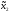 0)
– ситуация равновесия в игре
0)
– ситуация равновесия в игре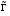 .
.
Упражнение.
Точку (7,2) можно сделать ситуацией равновесия на классе
{x1(x2),x2 [x1(x2)]}
Точку (2,7) можно сделать ситуацией равновесия на классе
{x2(x1),x1 [x2(x1)]}.
Замечание.
Точку из множества Парето можно сделать равновесной, если выигрыши игроков в ней оцениваются величиной не меньшей, чем их максимально гарантированные результаты, соответствующие их информированности. Этому условию удовлетворяет точка (7,2) на классе стратегий {x1(x2),x2 [x1(x2)]} и точка (2,7) на классе стратегий {x2(x1),x1 [x2(x1)]}.
Примеры на стратегиях!!!
Пример 1.
Покупатель продавец.
Стратегии:
продавец = {честно взвесил или обманул}
покупатель = {поверил или проверил}
Биматричная игра:
Покупатель
Верить
проверить
Честно взвесить 0,0 0, -1/2
Продавец
Обмануть 1,-1 -1,1
|
х1 а |
2 |
1 |
|
х2 |
1 |
2 |
x2= х2а , х2а = 2
|
х2 а |
1 |
2 |
|
x1 |
1 |
2 |
х1а = 1
(0,0) – в данном случае продавец честно взвесил товар, а покупатель ему верит, не проверяя.
(1,-1) – в данном случае продавец обманул покупателя, а покупатель не поверил ему.
(0,-1/2) – покупатель честно взвесил товар, но покупатель ему не поверил и решил проверить.
(-1,1) – продавец обманул покупателя, а тот решил проверить продавца.
1. Ситуации равновесия не всегда существуют.
х1а(x2)
|
обманул |
честно взвесил |
|
верит |
не верит |
х2а(x1)
|
честно взвесил |
обманул |
|
верит |
не верит |
Ситуации равновесия не существует, так как хотя бы одному игроку выгодно отклониться.
Пример 2. Семейный спор.
Жена
Футбол
балет
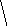
Футбол 2,1 0,0 Муж
Балет 0,0 1,2
(2,1) – в данном случае в выигрыше оказывается муж, так как он идет на футбол, причем вместе с женой.
(0,0) – в данном случае ни один из них не оказывается в выигрыше, так как муж не пошел женой на балет, а она не пошла с ним на футбол. То есть не провели вечер вместе, хотя планировали именно так.
(0,0) – опять не в выигрыше.
(1,2) – в данном случае в выигрыше оказывается жена, так как они пошли на балет вместе.
|
х1 а |
1 |
2 |
|
х2 |
1 |
2 |
х2а = 2
|
х1 |
1 |
2 |
|
х2 а |
1 |
2 |
х1а = 1
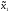 = 1, х2=
1 (Ф)
= 1, х2=
1 (Ф)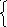
1, х2 = 2 (Б)
В данном случае существует 2 ситуации равновесия: (1,2) и (2,1). Вопрос в том, кто берет на себя инициативу установления равновесия. Этот вопрос решается только обсуждениями в динамике или учитывая, кто в семье главный.
2. Ситуация равновесия не всегда может быть принципом оптимальности для бескоалиционной игры, так как партнером нужно договориться, какую ситуацию выбрать.
Пример 3. Реклама.
