
- •Московский Государственный открытый университет
- •Понятие хозяйственного механизма
- •Базовая модель
- •Общая схема формализации процессов моделирования хозяйственного механизма
- •Лекция 2 Базовая модель в контексте формализованной схемы моделирования хозяйственного механизма
- •Производственные функции. Агрегирование и дезагрегирование
- •Лекция 3 Синергетический эффект
- •Эффективность создания совместного производства (системы)
- •Механизм инноваций
- •Лекция 4 Многокритериальные задачи
- •Поиск эффективных точек
- •Лекция 5
- •Формализация основных понятий Теории Игр.
- •Принцип Оптимальности
- •Принятие решений
- •Принцип Оптимальности
- •2 Фирма
- •1 Фирма
- •Роль информированности. Формализация информированности в виде стратегии
- •Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
- •Формальное определение
- •Информационное расширение игры
- •Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
- •Ситуация равновесия по Нэшу в информационном расширении игры
- •2 Фирма
- •1 Фирма
- •Лекция 7 Иерархические системы управления
- •Обобщенный принцип максимального гарантированного результата (оп мгр)
- •Иерархическая игра (игра Гермейера)
- •Экономическая интерпретация иерархических игр г1, г2и г3
- •Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
- •2.Аналог игры
- •Лекция 9 Динамические модели принятия решений
- •Слабоустойчивые совместные решения по ю. Б. Гермейеру
- •Динамическая модель принятия решений с непрерывным временем
- •Оптимизация процесса контроля (наблюдения)
- •Литература
- •Лекция 10 Управление ису при неточном знании параметров подсистем
Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
Итак мы провели анализ элементарной ячейки иерархической системы управления (ИСУ). Сначала был рассмотрен вариант взаимодействия элементов, находящихся на одном уровне иерархии, затем – на разных уровнях.
В достаточно общей постановке анализ двухуровневой статической модели ИСУ сводится к решению игры n+1 лица, определяемой следующими параметрами:
1⁰
Задано множество игроков
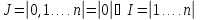 .
.
Подмножества
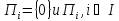 определяют верхний и нижний уровни
иерархии. Центр (Игрок
определяют верхний и нижний уровни
иерархии. Центр (Игрок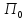 )
обладаем правом первого хода, т.е. первым
выбирает и сообщает своюстратегию
элементу нижнего уровня
)
обладаем правом первого хода, т.е. первым
выбирает и сообщает своюстратегию
элементу нижнего уровня
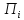 .
.
2⁰
Вектора
 определяют управляющие параметры
определяют управляющие параметры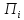 .
. набор управлений всех элементов нижнегоуровня,
набор управлений всех элементов нижнегоуровня,
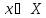 .
.
3⁰
На множестве
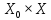 заданы целевые функции:
заданы целевые функции:
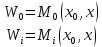
Интересы
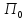 описываются стремлением к максимизации
этих функций.
описываются стремлением к максимизации
этих функций.
4⁰
Взаимная информированность
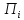 соответствует порядку ходов и определяет
их стратегии
соответствует порядку ходов и определяет
их стратегии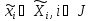 .
.
5 Для
Для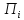 ,
, определены правила поведения (принципы
оптимальности), которые позволяют центру
определены правила поведения (принципы
оптимальности), которые позволяют центру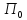 оценить множество возможных ответов
элементов нижнего уровня:
оценить множество возможных ответов
элементов нижнего уровня: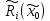 .
.
Сформулированная игра многих лиц является обобщением игр двух лиц, рассмотренных ранее. Исследование значительно упрощается, если модель ИСУ имеет веерную структуру.
ИСУ
называетсявеерной, если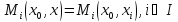 .Функции выигрыша
элементов нижнегоуровня
таких ИСУ зависятот управления
центра и своего управления и не зависят
от управлений своих соседей.
.Функции выигрыша
элементов нижнегоуровня
таких ИСУ зависятот управления
центра и своего управления и не зависят
от управлений своих соседей.
Задача
рассматривается в интересах центра.
Рассмотрим данный тип игр на примере
игр, аналогичных
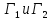 .
.
Аналог игры
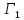
Правило
1.1 В этом случае ,
т.е. центр не имеет информации о действиях
подчиненного до своего выбора.
,
т.е. центр не имеет информации о действиях
подчиненного до своего выбора.
Правило
1.2 Для любого
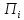 выбирает
выбирает
Правило
1.3
 выбирает
выбирает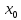 из условия МГР.
из условия МГР.
Правила 1.1-1.3 получены путем конкретизации параметров 1⁰-5⁰ игры общего вида.
Теорема 1.
Решение
сформулированной игры (типа
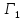 )
эквивалентно для центра решению игры
)
эквивалентно для центра решению игры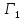 для двух лиц, где один игрок
для двух лиц, где один игрок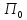 ,
а второй игрок – игрок с функцией
,
а второй игрок – игрок с функцией
выигрыша
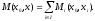
Доказательство.
Определим
множество
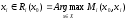 Тогда МГР игрока
Тогда МГР игрока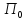 в игре
в игре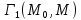 равен :
равен :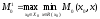 .
.
С
другой стороны для исходной игры с nподчиненными имеем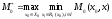
Утверждение
Теоремы 1 (равенство
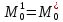 )
следует из соотношениясправе
)
следует из соотношениясправе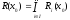 дливогов силу очевидного равенства
дливогов силу очевидного равенства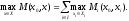
Теорема доказана.
2.Аналог игры
Правило
2.1 В этомслучае
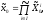
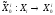 ,т.е. центр имеет информацию о выборе
подчиненных и использует в качестве
стратегии функции
,т.е. центр имеет информацию о выборе
подчиненных и использует в качестве
стратегии функции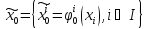 .
Здесь
.
Здесь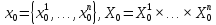 ,
т.е. управление центра разбивается наnуправлений
,
т.е. управление центра разбивается наnуправлений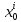 ,
а функция выигрыша
,
а функция выигрыша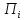 имеет вид
имеет вид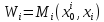 .
.
Правило
2.2 Игрок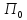 ходит первым, т.е. выбирает и сообщаеткаждому
ходит первым, т.е. выбирает и сообщаеткаждому
 стратегию
стратегию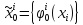 .
.
Правило
2.3 Игроки выбирают в силу своего правила поведения
выбирают в силу своего правила поведения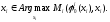
Правило
2.4 Оптимальную стратегию выбирает из ОПМГР.
выбирает из ОПМГР.
Определим некоторые вспомогательные конструкции.
Введем
параметры
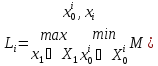 )
)
Аналогично играм двух лиц определим взаимовыгодные множества исходов:
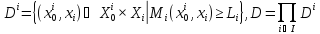
Обозначим
через
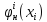 - стратегиинаказания:
- стратегиинаказания:
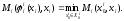
Определим
исход
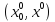 :
: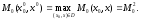
Теорема 2.
Пусть
элементы нижнего уровня доброжелательны
к центру, тогда МГР
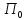 равен
равен ,
и достигается на стратегии:
,
и достигается на стратегии:
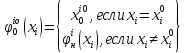
Доказательство
(аналогично доказательству теоремы
для игры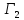 в случае игры двух лиц).
в случае игры двух лиц).
Докажем, что результат
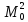 гарантирован.
гарантирован.
Пусть
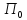 использует
стратегию
использует
стратегию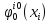 .
Если
.
Если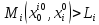 , то рациональный ответ
, то рациональный ответ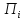 - выбрать
- выбрать , так как в противном случае игрок
, так как в противном случае игрок будет наказан и не получит больше
будет наказан и не получит больше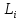 .
Если
.
Если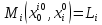 ,
то в силу доброжелательности игрок
,
то в силу доброжелательности игрок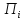 опять же выберет
опять же выберет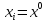 .
.
Покажем, что больше
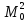 центр получить не сможет.
центр получить не сможет.
По
определению
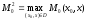 ,
поэтому больше
,
поэтому больше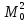 центр сможет получить только внеD.
Но внеDхотя бы один
подчиненный получит меньше
центр сможет получить только внеD.
Но внеDхотя бы один
подчиненный получит меньше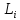 , что он не допустит. Следовательно,
центр получить больше
, что он не допустит. Следовательно,
центр получить больше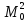 не сможет.
не сможет.
Определение:
ИСУ идеально согласованна, если
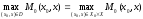
В идеально согласованной ИСУ центр на оптимальной стратегии получает глобальный максимум.
Пример ИСУ
Пусть у нас функции выигрышей игроков и управления имеют следующую зависимость:
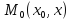 ,
,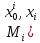 )
,где
)
,где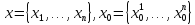 . Будем считать, что
. Будем считать, что
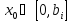 -выплаты центра
-выплаты центра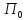 элементу
элементу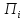 за произведенную продукцию
за произведенную продукцию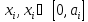 .
.
Пусть выполнены условия монотонности.
Функция
 строго монотонно растет по
строго монотонно растет по , а по
, а по - строго монотонно убывает. Аналогично
- строго монотонно убывает. Аналогично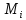 от любого поощрения
от любого поощрения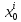 строго
монотонно растет, а от затрат убывает.
строго
монотонно растет, а от затрат убывает.
Очевидно
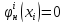 – стратегия наказания центра.
– стратегия наказания центра.
Максимальные
гарантированные результаты подчиненных
равны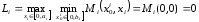
Заметим,
что ситуация (0,0) является ситуацией
равновесия по Нэшу на классе управлений.
Пусть точка
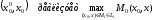 ,где
взаимовыгодное множествоDопределяется ограничением
,где
взаимовыгодное множествоDопределяется ограничением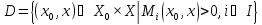 .
Тогда оптимальная стратегия будет
выглядеть следующим образом:
.
Тогда оптимальная стратегия будет
выглядеть следующим образом:
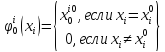
Замечание 1
Если
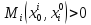 , то гарантия получения
, то гарантия получения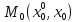 очевидна.
очевидна.
Если
же существует i такое, что
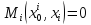 ,
,
то
всегда можно найти
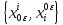 ,
такое что
,
такое что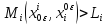 ,
,

(Либо как и ранее можно предположить доброжелательность Пi ).
Замечание 2
На практике используется стратегия неполного наказания.
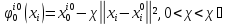 То есть степень наказания непрерывно
зависит от величины отклонения от «
плана».
То есть степень наказания непрерывно
зависит от величины отклонения от «
плана».
Замечание 3
Центр
использует класс стратегий
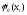 , которые сообщает нижнему уровню, а
, которые сообщает нижнему уровню, а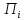 используют стратегии вида
используют стратегии вида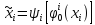 .
.
Именно
на этом классе стратегий реализуем
ситуацию равновесия, которая приводит
к хорошему исходу
 .
Отметим, что классическая ситуация
равновесия по Нэшу существует и
единственна:
.
Отметим, что классическая ситуация
равновесия по Нэшу существует и
единственна: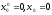 Её экономический смысл- полное закрытие
производства.
Её экономический смысл- полное закрытие
производства.
Замечание 4
Весь математический аппарат обобщается на иерархические системы управления с m уровнями.
Каким
же образом они обобщаются? Рассмотрим
ИСУ вида:(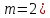
П0
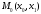

П1

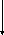
П2
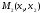
Вычислим гарантированный результат нижнего уровня.
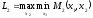
Единственная тонкость- это как вычисляется гарантированный результат в промежуточных звеньях.
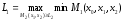
Здесь отслеживаются интересы нижнего уровня.
Тогда оптимальный результат верхнего уровня вычисляется с учетом интересов элементов нижнего уровня.

Замечание 5
Если мы имеем дело с ИСУ не веерного типа.
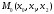

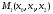
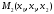
Либо, если ИСУ изначально веерного
типа, но стратегии П0, сообщаемые Пi,
зависят еще и от выборов других
подчиненных, например
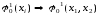 .
.
Тогда выигрыш П1 зависит не только от x1, но и от выбора x2:
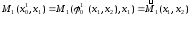
Для таких задач помимо правила 2.50добавляется (2.5”), которое формулируется следующим образом.
Правило
2.5”Центр
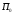 в соответствии со своими интересами
может устанавливать порядок ходов и
процедуры обменаинформацией
в том числе, передавать
необходимую информацию каждому
в соответствии со своими интересами
может устанавливать порядок ходов и
процедуры обменаинформацией
в том числе, передавать
необходимую информацию каждому
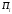 о действиях его партнеров.
о действиях его партнеров.
То
есть если вместо
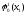
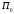 передает
передает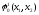 ,
то он должен обеспечить информацией
П1о выборе П2
,
то он должен обеспечить информацией
П1о выборе П2
Пример.
Пусть
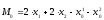
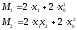
Управления
П0: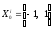 ,где
-1-штраф, +1-поощрения
,где
-1-штраф, +1-поощрения
Управления
Пi: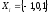 ,i=1,2
,i=1,2
МГР
для первого игрока П1
равен:
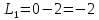
Аналогично
для П2 имеем: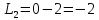
Следовательно,
в этой задаче
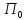 получает глобальный максимум в точке
получает глобальный максимум в точке
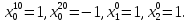
При этом
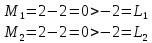
Для
гарантии выбора
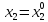 ,
,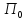 должен заблаговременно сообщить
информацию о
должен заблаговременно сообщить
информацию о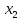 игроку
игроку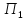 .
.
Замечание 6
Вместо
того чтобы использовать сложный класс
стратегий и использовать соответствующий
обмен информацией, в некоторых моделях
центр сообщает простые стратегии
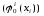 и
рассчитывает, что элементы нижнего
уровня придерживаются ситуации равновесия
по Нэшу (классической ситуации равновесия
по Нэшу).
и
рассчитывает, что элементы нижнего
уровня придерживаются ситуации равновесия
по Нэшу (классической ситуации равновесия
по Нэшу).
