Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры

В теории игр равновесием Нэша (названным в честь Джона Форбса Нэша, который предложил его) называется тип решений игры двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив своё решение в одностороннем порядке, когда другие участники не меняют решения.

Такая совокупность стратегий выбранных участниками и их выигрыши называются равновесием Нэша.

Концепция равновесия Нэша (РН) впервые использована не Нэшем; Антуан Огюст Курно показал, как найти то, что мы называем равновесием Нэша, в игре Курно. Соответственно, некоторые авторы называют его равновесием Нэша-Курно.

Однако Нэш первым показал в своей диссертации Некооперативные игры (1950), что равновесия Нэша должны существовать для всех конечных игр с любым числом игроков. До Нэша это было доказано только для игр с 2 участниками с нулевой суммой Джоном фон Нейманом и Оскаром Моргенштерном (1947).

Формальное определение

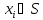Допустим, (S,F) — игра n лиц в нормальной форме, гдеS— набор чистых стратегий, аF— набор выигрышей. Когда каждый игроквыбирает стратегиюв профиле стратегий ,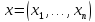игрокiполучает выигрыш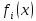. Заметьте, что выигрыш зависит от всего профиля стратегий: не только от стратегии, выбранной самим игрокомi, но и от чужих стратегий.

Профиль стратегий является равновесием по Нэшу, если изменение своей стратегии не выгодно ни одному игроку, то есть для любого i

.

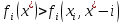Игра может иметь равновесие Нэша в чистых стратегиях или в смешанных (то есть при выборе чистой стратегии стохастически с фиксированной частотой). Нэш доказал, что если разрешить смешанные стратегии, тогда в каждой игре n игроков будет хотя бы одно равновесие Нэша.

Информационное расширение игры

Пусть задана исходная игра Г=<X₁,X₂,M₁,M₂>, тогда игра

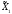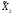
I=<X1,X2,π,M1(x1,x2),M2(x1,x2)называется информационным расширением игры, если существует проекция π:× X₁×X_2, обладающая следующими свойствами:

1) Каждой паре стратегий (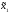,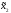) × 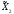ставит в соответствие пару управлений (исходов) (x₁,x₂) X₁×X_{2 ,} т.е. (x1 ,x2 ) ---->(x1,x2 )

2) Множество стратегий содержит стратегии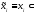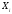, т.е. стратегии – управления, не использующие информации.

3) Функции выигрыша в игре 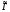вычисляются по правилу:

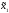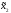_i(,) =M_i(π (,))

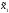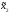Не для любых множеств стратегий выполняется свойство (1), а следовательно и свойства (2) и (3).

Например, возьмем пару {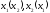}. В этом случае игрок 1 знает о выборе второго, а игрок 2 одновременно знает выбор первого - противоречие. Следовательно, пара {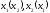} «физически» не реализуема.

Свойство (2) заключается в следующем:

Игроки могут использовать стратегии, для выбора которых не требуется учета информации, но это, как правило, нецелесообразно (приводит к потере выигрыша).

Выигрыши в игре 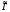определяются по свойству (3) равенством:

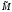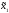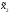_i(,) =M_i( π (,))

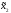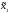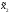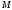Т.е. сначала стратегии (,) проектируются во множество управлений (исходов) - (x₁,x₂) X₁×X₂, а затем вычисляются значения_i(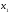,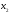), как и в игре Г.