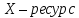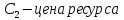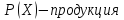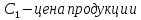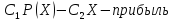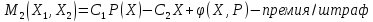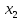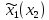- •Московский Государственный открытый университет
- •Понятие хозяйственного механизма
- •Базовая модель
- •Общая схема формализации процессов моделирования хозяйственного механизма
- •Лекция 2 Базовая модель в контексте формализованной схемы моделирования хозяйственного механизма
- •Производственные функции. Агрегирование и дезагрегирование
- •Лекция 3 Синергетический эффект
- •Эффективность создания совместного производства (системы)
- •Механизм инноваций
- •Лекция 4 Многокритериальные задачи
- •Поиск эффективных точек
- •Лекция 5
- •Формализация основных понятий Теории Игр.
- •Принцип Оптимальности
- •Принятие решений
- •Принцип Оптимальности
- •2 Фирма
- •1 Фирма
- •Роль информированности. Формализация информированности в виде стратегии
- •Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
- •Формальное определение
- •Информационное расширение игры
- •Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
- •Ситуация равновесия по Нэшу в информационном расширении игры
- •2 Фирма
- •1 Фирма
- •Лекция 7 Иерархические системы управления
- •Обобщенный принцип максимального гарантированного результата (оп мгр)
- •Иерархическая игра (игра Гермейера)
- •Экономическая интерпретация иерархических игр г1, г2и г3
- •Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
- •2.Аналог игры
- •Лекция 9 Динамические модели принятия решений
- •Слабоустойчивые совместные решения по ю. Б. Гермейеру
- •Динамическая модель принятия решений с непрерывным временем
- •Оптимизация процесса контроля (наблюдения)
- •Литература
- •Лекция 10 Управление ису при неточном знании параметров подсистем
Иерархическая игра (игра Гермейера)
Иерархическая игра определяется следующими правилами (предполагается, что игрок 1 – начальник, игрок 2 – подчиненный):
Игрок 1 знает все параметры модели игрока 2, то есть множество
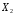 и функцию выигрыша
и функцию выигрыша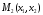 .
.Игрок 1 делает свой ход первым, то есть выбирает стратегию
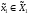 и сообщает информацию о ней игроку 2.
и сообщает информацию о ней игроку 2.Игрок 2 при известной ему стратегии
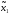 выбирает
выбирает ,
то есть максимизирует свой критерий.
,
то есть максимизирует свой критерий.При наличии неопределенных факторов (в данном случае – неоднозначного выбора 2-го игрока из множества
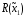 )
игрок 1 действует исходя из ОП МГР (4), а
в случае доброжелательности игрока 2
в соответствии с (6).
)
игрок 1 действует исходя из ОП МГР (4), а
в случае доброжелательности игрока 2
в соответствии с (6).
На основании этих предположений в зависимости от информации о выборах 2-го игрока, которую игрок 1 имеет или ожидает иметь, формулируются разные игры. Рассмотрим их.
Игра
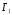 .
В этой игре:
.
В этой игре:
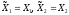 ,
то есть ни один из игроков заранее не
знает о выборе другого. Здесь игрок 1
выбирает
,
то есть ни один из игроков заранее не
знает о выборе другого. Здесь игрок 1
выбирает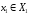 и сообщает об этом игроку 2, а он в свою
очередь выбирает
и сообщает об этом игроку 2, а он в свою
очередь выбирает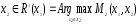 (множество точек, которое доставляет
максимум функции
(множество точек, которое доставляет
максимум функции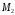 )
)
Тогда в этой игре МГР 1-го игрока:

 - оптимальное управление (стратегия),
определяемая условием:
- оптимальное управление (стратегия),
определяемая условием:
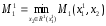
В случае доброжелательности игрока 2 МГР игрока 1 равен
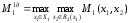 ,
,
а оптимальная стратегия определяется из условия
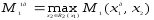
Можно «стимулировать»
доброжелательность, используя побочный
платеж
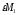 .
В этом случае, функция выигрыша игрока
2 примет вид:
.
В этом случае, функция выигрыша игрока
2 примет вид:
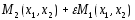
Аналогичный прием можно
использовать в играх
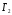 и
и
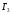 (смотри далее).
(смотри далее).
Игра
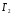 .
В этой игре
.
В этой игре
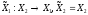 ,
то есть игрок 1 перед выбором своей
стратегии будет знать выбор игрока 2.
Таким образом, стратегия 1-го игрока
выглядитследующим
образом:
,
то есть игрок 1 перед выбором своей
стратегии будет знать выбор игрока 2.
Таким образом, стратегия 1-го игрока
выглядитследующим
образом:
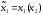
Игра
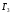 .
В этой игре
.
В этой игре
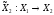 ,
то есть игрок 2 перед выбором
,
то есть игрок 2 перед выбором знает
знает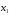 .
Стратегия 2-го игрока:
.
Стратегия 2-го игрока:
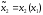
Однако первый игрок знает
правило поведения 2-го (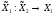 )
и поэтому его стратегия будет такой:
)
и поэтому его стратегия будет такой:
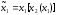
Замечание 5.
В играх
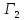 и
и
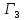 оптимальный выигрыш 1-го игрока
определяется формулой (4). Таким образом,
решение игр
оптимальный выигрыш 1-го игрока
определяется формулой (4). Таким образом,
решение игр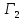 и
и
 сводится к вариационным и более сложным
задачам. Однако далее мы конструктивно
определим решение этих игр на исходном
множестве управлений
сводится к вариационным и более сложным
задачам. Однако далее мы конструктивно
определим решение этих игр на исходном
множестве управлений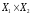 .
.
Замечание 6.
Можно рассматривать игры
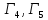 ,
,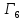 ,...
,...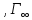 .
Но оказывается, что ситуация 4 сводится
к ситуации 2, ситуация 5 сводится к
ситуации 3, а ситуация 6 сводится к
ситуации 4 и т.д., то есть;
.
Но оказывается, что ситуация 4 сводится
к ситуации 2, ситуация 5 сводится к
ситуации 3, а ситуация 6 сводится к
ситуации 4 и т.д., то есть;
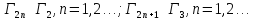
Из этого следует, что просчет вариантов действий в глубину не следует делать больше трех, дальше все повторяется.
Экономическая интерпретация иерархических игр г1, г2и г3
Игра
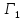 .
Эта игра моделирует процесс управления
ценами на произведенную продукцию и
затрачиваемые ресурсы:
.
Эта игра моделирует процесс управления
ценами на произведенную продукцию и
затрачиваемые ресурсы:
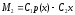
где x – ресурс,
p(x) – продукция,
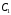 - цена на продукцию,
- цена на продукцию,
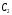 - цена на ресурс.
- цена на ресурс.
Пусть
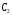 фиксирована.
фиксирована.
Найти
 такую, что
такую, что было выгодно игроку 2.Из необходимого
условия экстремума имеем:
было выгодно игроку 2.Из необходимого
условия экстремума имеем:
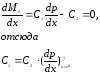
Если
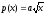 ,
то
,
то
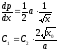 ,
,
Игра
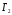 .
Эта игра моделирует процесс управления
штрафами, поощрениями.
.
Эта игра моделирует процесс управления
штрафами, поощрениями.
Опять пусть
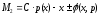
«+» - премия, «-» - штраф, налог.
Тогда стимулирование выбора
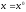 можно, например, произвести следующим
образом (для определенности
можно, например, произвести следующим
образом (для определенности - штраф)
- штраф)
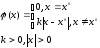
Игра
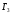 .
Эта игра моделирует процесс выдачи
ресурсов, кредитования под обоснованную
программу их использования
.
Эта игра моделирует процесс выдачи
ресурсов, кредитования под обоснованную
программу их использования
Пусть игрок 1 стимулирует
реализацию ситуации
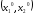 .
Тогда он должен стимулировать игрока
2 выбрать программу
.
Тогда он должен стимулировать игрока
2 выбрать программу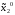 использования выделяемого ресурса:
использования выделяемого ресурса:
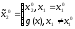
где
 - произвольная функция.
- произвольная функция.
Игроку 1 важно только, что
выделяемый ресурс
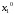 используется игроком 2 следующим образом
используется игроком 2 следующим образом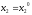 .
Поэтому оптимальная стратегия игрока
1 имеет вид
.
Поэтому оптимальная стратегия игрока
1 имеет вид
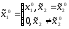
Как уже
Решение
игр
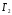 и
и
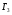 сводится к вариационным и более сложным
задачам. Однако далее мы конструктивно
определим решение этих игр на исходном
множестве управлений
сводится к вариационным и более сложным
задачам. Однако далее мы конструктивно
определим решение этих игр на исходном
множестве управлений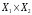 .
.
Игра Г2.
В
этой игре
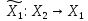 ,
т.е. игрок 1 до выбора
,
т.е. игрок 1 до выбора
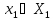 имеет информацию о
имеет информацию о
 .
.
Поэтому стратегии игрока 1 – функции
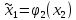
Для
игрока 2 имеем
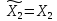
Вспомогательные конструкции.
Стратегия наказания:
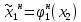 определяется из условия:
определяется из условия:
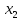
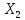
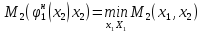
Максимально гарантированный результат (МГР) подчиненного равен
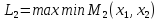
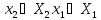
Множество исходов выгодное подчиненному

Исходы (x1, x2 ) вне этого множества не устраивают игрока 2 и он всегда может добиться выигрыша не меньше, чем L2 , выбирая x2 = xˆ2 из условия
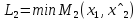
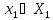
Определим
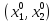 из равенства
из равенства

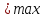
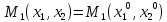
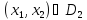
Наконец определим
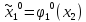 =
=
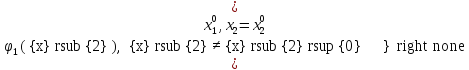
Отметим,
что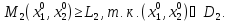
Теорема 1.
При
условии доброжелательности , оптимальный
выигрыш игрока 1
в игре Г2,равен
К2,
а
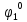 (
(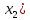 -
его оптимальная стратегия.
-
его оптимальная стратегия.
Доказательство:
При
известной стратегии
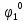 (
(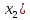 игрок 2
получит:
игрок 2
получит:
-
если
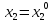 ,
то
,
то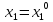 и
и
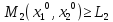 .
.
-
если же игрок 2
выберет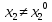 , то его выигрыш не
превысит
, то его выигрыш не
превысит

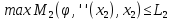 .
.
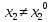
Если
 , то множество R2
(
, то множество R2
( )
состоит из единственной точки
)
состоит из единственной точки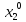 .
.
В
случае
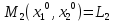 множество
R2
(
множество
R2
(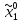 )
содержит выборыx2
, в том числе
)
содержит выборыx2
, в том числе
 , эквивалентные для игрока 2
. В силу доброжелательности
игрока 2 ,
он выберет точку
, эквивалентные для игрока 2
. В силу доброжелательности
игрока 2 ,
он выберет точку
 - выгодную для игрока
1.
- выгодную для игрока
1.
Итак, в условиях
теоремы игроку1
гарантируется исход
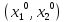 , приводящий к выигрышу
, приводящий к выигрышу
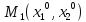 =
=
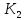
Покажем, что К2 - максимальный гарантированный выигрыш.
Действительно,
если исход (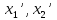 )
приводит к
)
приводит к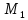 (
(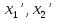 )
>
)
>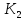 ,
,
то он лежит вне множества D2
по определению
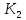
Но вне множества D2 выигрыш игрока 2 оценивается величиной
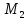 (
(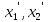 )
)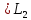 .
.
Это
не выгодно игроку 2
и он всегда может
выбором
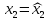 получить
получить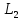 .
.
Теорема доказана.
Замечание 2.
Условие доброжелательности
может быть опущено, если множество
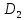 является
замыканием не пустого множества
является
замыканием не пустого множества
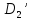 =
{(
=
{(
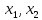 )
)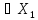 ×
×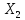 |
|
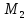 (
(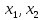 )
>
)
>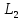 }
}
Действительно,
в этом случае даже, если
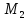 (
(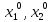 )
=
L2,
можно «скорректировать»
оптимальную стратегию, заменив ее
стратегией
)
=
L2,
можно «скорректировать»
оптимальную стратегию, заменив ее
стратегией
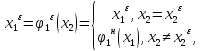
Где
точка (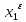 ,
,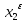 )
удовлетворяет условиям:
)
удовлетворяет условиям:
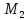 (
(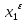 ,
,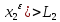
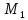 (
(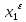 ,
,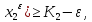
 ,
,
величина
 определяет затраты игрок 1 на стимуляцию
игрока 2.
определяет затраты игрок 1 на стимуляцию
игрока 2.
Механизмом такой стимуляции может служить «побочный платеж».
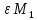 (
(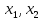 )
обещанный начальником
подчиненному.
)
обещанный начальником
подчиненному.
Игра
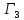
В
этой игре игрок 2 знает выбор игрока 1
до своего выбора
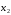 ,
т.е.:
,
т.е.: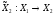 ,
,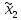 =
=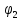 (
(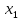 ).
В свою очередь игрок 1 знает такое правило
поведения игрока 2, т.е.
).
В свою очередь игрок 1 знает такое правило
поведения игрока 2, т.е.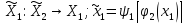
Вспомогательные конструкции.
Определим МГР игрока 2:
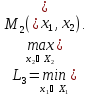
Далее определим стратегию наказания (стратегию наихудшую для игрока 2)
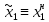
из условия
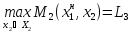
В
игре
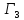 взаимовыгодное множество
взаимовыгодное множество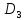 определяется равенством
определяется равенством
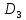 = {(
= {(
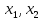 )
)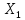 ×
×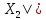
 ≥
≥
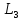 }
}
Напомним,
что всегда
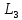 ≥
≥
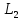 ,
поэтому
,
поэтому
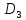
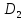 .
Определим исход (
.
Определим исход (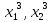 )
из условия
)
из условия
К3
=
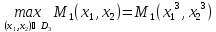
Построим стратегию игрока 2:
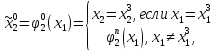
где
 произвольная
функция.
произвольная
функция.
Оптимальная стратегия игрока 1имеет вид:

Содержательно
игрок 1 выберет
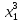 (выдает кредит), если игрок 2 использует
этот кредит выбором
(выдает кредит), если игрок 2 использует
этот кредит выбором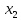 =
=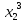 ,при
этом игрок 2 получает
,при
этом игрок 2 получает (
(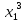 ,
, ) ≥
) ≥
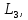
В
противном случае игрок 1 выбирает
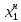 и игрок 2 не получит
больше
и игрок 2 не получит
больше
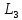 .
.
Теорема 2.
При
условии доброжелательности игрок 2
оптимальный выигрыш игрока 1 в игре
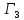 равен
равен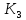 ,
а
,
а
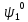 – его оптимальная стратегия.
– его оптимальная стратегия.
Доказательство.
Аналогично доказательству теоремы 1.
Замечание 1 и 2 к теореме 1 справедливы и для теоремы 2.
Кроме
того, в силу
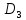 ≤
≤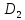 имеем
имеем
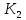 ≥
≥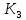 ,
то есть выигрыш игрока 1 в игре
,
то есть выигрыш игрока 1 в игре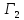 больше или равен его выигрышу в игре
больше или равен его выигрышу в игре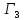 .
.
Упражнение.
Докажите,
что если в антагонистической игре
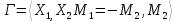 ,
,
существует
седловая точка, то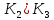
Пример.

Ранее на этом примере, мы строили ситуации равновесия на сложных стратегиях. Теперь проиллюстрируем решение иерархических игр.
Игра
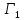
Определим множества рациональных ответов игрока 2.
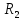 (1) = 3,
(1) = 3,
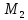 (1,3) = 7,
(1,3) = 7,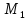 (1,3) = 2
(1,3) = 2
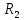 (2) = 2,
(2) = 2,
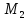 (2,2) = 4,
(2,2) = 4,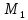 (2,2) = 4
(2,2) = 4
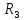 (3) = 2,
(3) = 2,
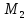 (3,2) = 3,
(3,2) = 3,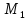 (3,2) = 0
(3,2) = 0
Тогда
max
min
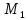 (
(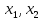 )
= max [2,4,0]=4
)
= max [2,4,0]=4
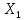 ={1,2,3}
={1,2,3}
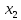
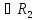 (
(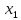 )
)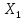 ={1,2,3}
,
={1,2,3}
,
при
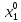 =2,
=2,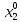 =2
=2
Замечание.
Решение
игры
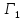 совпало с ситуацией равновесия по Нэшу
на управлениях. В общем случае в этой
игре можно получить выигрыш, равный
выигрышу в наилучшей для игрока ситуации
равновесия и даже больше.
совпало с ситуацией равновесия по Нэшу
на управлениях. В общем случае в этой
игре можно получить выигрыш, равный
выигрышу в наилучшей для игрока ситуации
равновесия и даже больше.
Игра
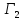
В
этом случае
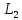 = max
min
= max
min
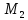 (
(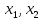 )
= 0,
)
= 0,
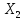
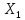

φ1н(х2)
=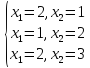


К2
=
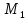 (
(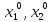 )
=
)
=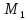 (3,1) = 7, что соответствует глобальному
максимуму М1.
(3,1) = 7, что соответствует глобальному
максимуму М1.
Оптимальная
стратегия игрока 1:
φ10(х2)
=
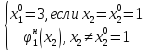
Выигрыш
игрока 2 равен
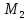 (
(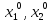 )
=
)
=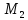 (3,1) = 2>0 =
(3,1) = 2>0 =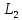
Игра Г3.
В
этой игре
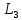 = min
max
= min
max
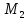 (
(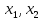 )
= 3
)
= 3
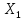
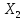
Стратегия наказания
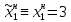
Оптимальный выигрыш игрока 1 определяется следующим образом:
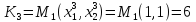
Построим стратегию игрока 2:
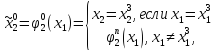
где
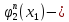 произвольная
функция.
произвольная
функция.
Оптимальная стратегия игрока 1имеет вид:

При
этом игрок 2 получит
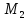 (1,1) = 6 > 3=
(1,1) = 6 > 3=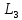 .
.
Заметим,
что в этом примере
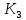 = 6 < 7 =
= 6 < 7 =
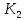
Пример:
У 1 игрока - 3 стратегии
2 игрока - 3 стратегии

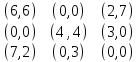
1игрок выбирает строки
2 игрок выбирает столбцы
Слева - выигрыш 1
Справа – выигрыш 2
max гарантированный результат:
При условии, что 1 игрок выбирает строку
Отметим по строкам, где выигрыш 2 игрока max
Отметим по столбцам, где выигрыш 1 игрока max
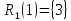
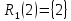 Ст1
= 4
Ст1
= 4
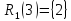
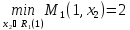
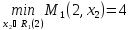
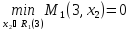
Пример:

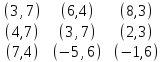
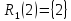 Ст1
= 3
Ст1
= 3
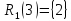 max
1игрока из отмеченных
max
1игрока из отмеченных
Пример:
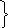
 отрезки
отрезки
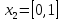

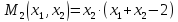
Решение:
Найдем
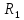
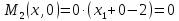
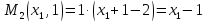
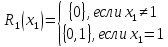
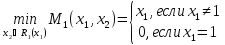
Y
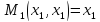
X
1
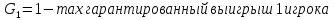
Пример:
Предприятие производит некую продукцию, для этого необходимо что-нибудь затратить
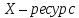
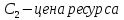
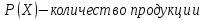
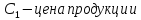

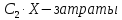
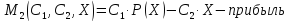
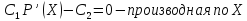
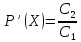
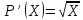
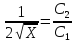
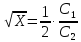
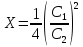
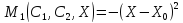
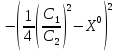

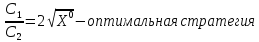
Пример:
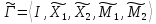
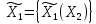
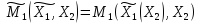
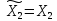
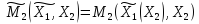
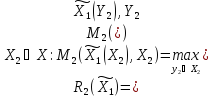
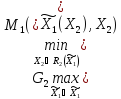
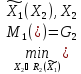


|
|
1 |
2 |
3 |
1 |
2 |
3
|
|
|
1 |
1 |
1 |
(6,6) |
(0,0) |
(2,7) |
|
1 |
1 |
2 |
(6,6) |
(0,0) |
(3,0) | |
|
1 |
1 |
3 |
(6,6) |
(0,0) |
(0,0) | |
|
1 |
2 |
1 |
(6,6) |
(4,4) |
(2,7) | |
|
1 |
2 |
2 |
(6,6) |
(4,4) |
(3,0) | |
|
1 |
2 |
3 |
(6,6) |
(4,4) |
(0,0) | |
|
1 |
3 |
1 |
(6,6) |
(0,3) |
(2,7) | |
|
1 |
3 |
2 |
(6,6) |
(0,3) |
(3,0) | |
|
1 |
3 |
3 |
(6,6) |
(0,3) |
(0,0) | |
|
2 |
1 |
1 |
(0,0) |
(0,0) |
(2,7) | |
|
2 |
1 |
2 |
(0,0) |
(0,0) |
(3,0) | |
|
2 |
1 |
3 |
(0,0) |
(0,0) |
(0,0) | |
|
2 |
2 |
1 |
(0,0) |
(4,4) |
(2,7) | |
|
2 |
2 |
2 |
(0,0) |
(4,4) |
(3,0) | |
|
2 |
2 |
3 |
(0,0) |
(4,4) |
(0,0) | |
|
2 |
3 |
1 |
(0,0) |
(0,3) |
(2,7) | |
|
2 |
3 |
2 |
(0,0) |
(0,3) |
(3,0) | |
|
2 |
3 |
3 |
(0,0) |
(0,3) |
(0,0) | |
|
3 |
1 |
1 |
(7,2) |
(0,0) |
(2,7) | |
|
3 |
1 |
2 |
(7,2) |
(0,0) |
(3,0) | |
|
3 |
1 |
3 |
(7,2) |
(0,0) |
(0,0) | |
|
3 |
2 |
1 |
(7,2) |
(4,4) |
(2,7) | |
|
3 |
2 |
2 |
(7,2) |
(4,4) |
(3,0) | |
|
3 |
2 |
3 |
(7,2) |
(4,4) |
(0,0) | |
|
3 |
3 |
1 |
(7,2) |
(0,3) |
(2,7) | |
|
3 |
3 |
2 |
(7,2) |
(0,3) |
(3,0) | |
|
3 |
3 |
3 |
(7,2) |
(0,3) |
(0,0) |
Ответ: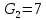
Пример:
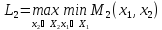
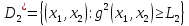
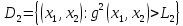
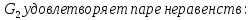
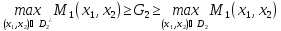

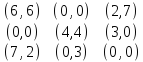
Пример:
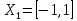
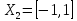
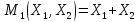
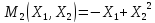
Определим
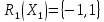
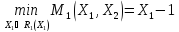
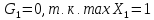
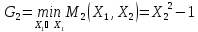

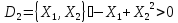
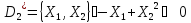


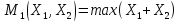

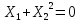
Ответ: (1,1)
Пример: