
- •Московский Государственный открытый университет
- •Понятие хозяйственного механизма
- •Базовая модель
- •Общая схема формализации процессов моделирования хозяйственного механизма
- •Лекция 2 Базовая модель в контексте формализованной схемы моделирования хозяйственного механизма
- •Производственные функции. Агрегирование и дезагрегирование
- •Лекция 3 Синергетический эффект
- •Эффективность создания совместного производства (системы)
- •Механизм инноваций
- •Лекция 4 Многокритериальные задачи
- •Поиск эффективных точек
- •Лекция 5
- •Формализация основных понятий Теории Игр.
- •Принцип Оптимальности
- •Принятие решений
- •Принцип Оптимальности
- •2 Фирма
- •1 Фирма
- •Роль информированности. Формализация информированности в виде стратегии
- •Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
- •Формальное определение
- •Информационное расширение игры
- •Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
- •Ситуация равновесия по Нэшу в информационном расширении игры
- •2 Фирма
- •1 Фирма
- •Лекция 7 Иерархические системы управления
- •Обобщенный принцип максимального гарантированного результата (оп мгр)
- •Иерархическая игра (игра Гермейера)
- •Экономическая интерпретация иерархических игр г1, г2и г3
- •Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
- •2.Аналог игры
- •Лекция 9 Динамические модели принятия решений
- •Слабоустойчивые совместные решения по ю. Б. Гермейеру
- •Динамическая модель принятия решений с непрерывным временем
- •Оптимизация процесса контроля (наблюдения)
- •Литература
- •Лекция 10 Управление ису при неточном знании параметров подсистем
Литература
1. Ю.Б. Гермейер «Игры с непротивоположными интересами». Изд-во «Наука». Москва. 1976.
Лекция 10 Управление ису при неточном знании параметров подсистем
Как
уже было отмечено для решения вопроса
о целесообразности построения
иерархической системы управления(ИСУ)
необходимо сравнить максимальный
гарантированный результат(МГР) центра
при централизованном и (частично)
децентрализованном способах управления.
При этом учитывается влияние неопределённых
факторов. Для этого будем считать, что
выигрыш центра определяется функцией
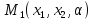 ,где
,где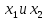 –управляющие
параметры центра; удовлетворяющие
ограничениям
–управляющие
параметры центра; удовлетворяющие
ограничениям ,i=1,2,
а α-неопределённый параметр, про который
центру известно только, что α∊А.
,i=1,2,
а α-неопределённый параметр, про который
центру известно только, что α∊А.
Тогда, следуя принципу МГР, центр оценивает свой выигрыш величиной

При
децентрализованном способе управления
центр передаёт нижнему уровню право
выбора параметра
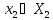 .Пусть
обмен информацией (в том числе и о
величине α) между уровнями приводит к
усложнению класса стратегий
.Пусть
обмен информацией (в том числе и о
величине α) между уровнями приводит к
усложнению класса стратегий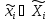 ,i=1,2.
,i=1,2.
Основываясь
на предположении о рациональном поведении
элементов нижнего уровня центр может
построить множество
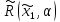 откликов
на свою стратегию. В этом случае принцип
МГР позволяет оценить выигрыш центра
величиной:
откликов
на свою стратегию. В этом случае принцип
МГР позволяет оценить выигрыш центра
величиной:
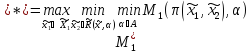
В
случае полной информированности А=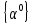 всегда имеет место неравенство
всегда имеет место неравенство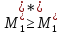 .
.
Однако
в более реальном случае наличия
неопределённости возможны любые из
трёх соотношений:
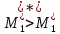 ,
,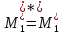 ,
,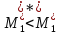 .
.
Выполнение
какого-либо одного из них определяется
,во-первых, самой моделируемой ситуацией
(функцией
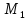 ,
множествами
,
множествами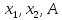 и, во-вторых, тем насколько удачен выбор
процедур обмена информацией (множествами
и, во-вторых, тем насколько удачен выбор
процедур обмена информацией (множествами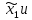
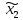 ).
).
В отличие от традиционных постановок задач принятия решений в условиях неопределённости будем изучать вопросы выбора рациональных решений в условиях наличия неопределённости, которую назовём субъективной.
Субъективная неопределённость характеризуется тем, что во-первых подсистемы имеют различную информированность о неопределённых факторах: о параметрах системы и её элементов, о влиянии на систему внешней среды, и во-вторых учитывается возможность и целесообразность обмена информацией о действиях элементов(т.е. о выборе ими управлений),о параметрах, описывающих влияние внешней среды.
Обмен информацией производится только в своих интересах, следовательно, не исключается
Далее
предполагается, что игрок 2 может сообщить
игроку 1 любое значение
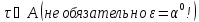 .Если
он не сообщает такой информации, то
игрок 1 формально, по своему усмотрению
присваивает этой величине какое-то
значение
.Если
он не сообщает такой информации, то
игрок 1 формально, по своему усмотрению
присваивает этой величине какое-то
значение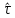 из множества А.
из множества А.
Итак,
будем считать что
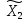 =
=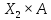 ,
,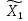 =
=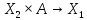 ,то есть игрок 1 до выбора
,то есть игрок 1 до выбора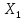 будет знать точную информацию о
будет знать точную информацию о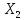 и какую-то информацию о
и какую-то информацию о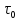 .
.
Итак,
рассмотрим игру
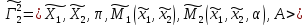 ,
где как и ранее проекция:
,
где как и ранее проекция:
𝜋: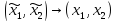 ,
,
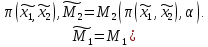
Введём некоторые обозначения
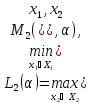
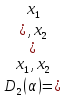 ,α)≥
,α)≥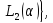
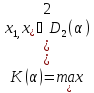
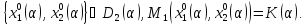
Стратегия наказания:
 (
(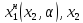 ,α)=
,α)=

Далее будем считать, что выполняются следующие условия:
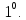 Знание
игроком 1 множества А не противоречит
объективному описанию модели, т.е.
истинное значение
Знание
игроком 1 множества А не противоречит
объективному описанию модели, т.е.
истинное значение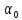 неопределённого параметра принадлежит
этому множеству
неопределённого параметра принадлежит
этому множеству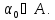
 Подчинённый
(игрок 2) доброжелателен к начальнику -
центру (игроку 1).Это условие как и ранее
можно заменить условиями, справедливыми
при всех α∊А
Подчинённый
(игрок 2) доброжелателен к начальнику -
центру (игроку 1).Это условие как и ранее
можно заменить условиями, справедливыми
при всех α∊А
-множества
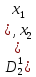
-замыкание
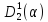 –множество
–множество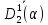 =
=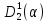 .
.
 Стратегия
наказания не зависит от параметра α
Стратегия
наказания не зависит от параметра α
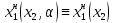 .
.
Построим стратегию
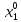 (
(
В
этой стратегии наказание реализуется,
если игрок 2 не сообщил информацию о
неопределённом параметре, т.е.
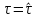 или сообщив информацию𝜏∊А
выбрал
или сообщив информацию𝜏∊А
выбрал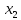 ≠
≠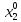 (𝜏).
(𝜏).
Замечание 2.Независимость стратегии наказания от неопределённого параметра не является жёстким ограничением для экономических моделей. Наказание-это выбор минимального значения цены и поощрения, либо максимального штрафа и т.д.
Замечание 3.Как и ранее предполагаем, что максимумы и минимумы в соответствующих выражениях достигаются.
Теорема.
В сформулированных условиях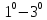 МГР игрока 1 равен
МГР игрока 1 равен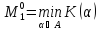 и
достигается путём выбора игроком 1
оптимальной стратегии
и
достигается путём выбора игроком 1
оптимальной стратегии
Доказательство.
Игрок 2 может выбрать лучшую для себя
пару
 ,
т.е. его выигрыш оценивается величиной
,
т.е. его выигрыш оценивается величиной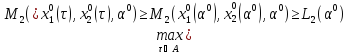
Если
же игрок 2 ослушается начальника-игрока
1,то при любом
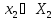
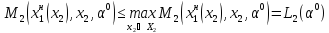
В силу доброжелательности или как часто бывает в силу неравенства
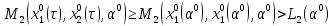
Игрок
2 с гарантией для игрока 1 выберет
наилучшую для себя пару
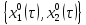 что в свою очередь гарантирует игроку
1 выигрыш
что в свою очередь гарантирует игроку
1 выигрыш

Итак,
результат
 гарантируется игроку 1. На больший
результат он рассчитывать не может, так
как при известном
гарантируется игроку 1. На больший
результат он рассчитывать не может, так
как при известном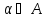 может получить не больше
может получить не больше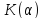 и рассчитывая на худшее для себя
и рассчитывая на худшее для себя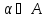 он не может ожидать выйгрыша более чем
он не может ожидать выйгрыша более чем
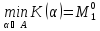
Теорема доказана.
Экономные процедуры обмена информацией.
Пусть
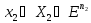 , где
, где размерность
вектора
размерность
вектора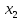 . Если
. Если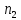 велико, то передача и анализ информации
о
велико, то передача и анализ информации
о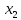 вызывает большие технические трудности
и экономические затраты.
вызывает большие технические трудности
и экономические затраты.
Поэтому
целесообразно исследовать вопрос об
эффективности принятия решений по
агрегированной информации, например,
вида
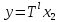 , гдеy– агрегированная
информация о выборе игрока 2,
, гдеy– агрегированная
информация о выборе игрока 2,
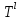 - линейный невырожденный оператор:
- линейный невырожденный оператор:
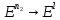 ,
,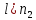 ,
,
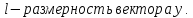
Например:
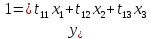
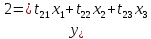
Здесь
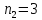 ,
,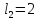
Обозначим
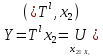
образ
множества
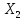 в пространстве
в пространстве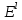 .
.
Таким
образом стратегия игрока 2 по прежнему
определяется выбором
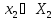 , то есть
, то есть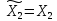
Множество
стратегий игрока 1 состоит из выбора
целого числа
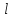 ,
,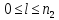 ;
;
Выбора
оператора
 и выбора функции
и выбора функции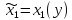 .
.
Кроме
того, зададим монотонно неубывающую
функцию, например, вида
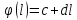 , которая имеет смысл платы за пользование
каналами связи, где
, которая имеет смысл платы за пользование
каналами связи, где
c– стоимость инфраструктуры, обеспечивающей передачу информации,
d– оплата одного канала связи,
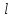 - число каналов связи(по размерности
вектора
- число каналов связи(по размерности
вектора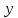 ).
).
Целью
игрока 1 является максимизация значения
функции

Поясним постановку и решение задачи на примере.
Пример:
Пусть функции выигрыша игроков линейны по их управлениям:
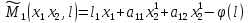
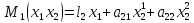 ,
,
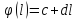 ,
,
Где уравнения игрока 1:
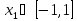 ,
, ,
,
А игрока 2:
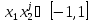 ,
,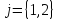 .
.
Наложим на параметры задачи ограничения:
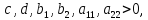
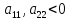 ,
,
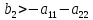
Последнее ограничение обеспечивает выигрыш игроку (в оптимальной точке), превышающий величину
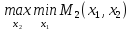
В нашей линейной модели
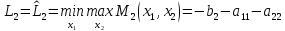
А стратегия наказания имеет вид:
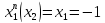
Обозначим
оптимальный выигрыш игрока 1 при
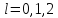 соответственно
соответственно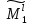 .
.
При
 получаем игру
получаем игру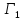 ,
решение которой имеет вид
,
решение которой имеет вид
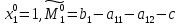
Оптимальный (рациональный) выбор игрока 2 определяется равенствами
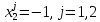
При
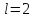 имеет игру
имеет игру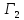 ,
в которой оптимальная стратегия игрока
1 имеет вид
,
в которой оптимальная стратегия игрока
1 имеет вид
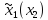 =
=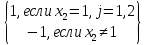
Оптимальный выигрыш игрока 1 равен

А выигрыш игрока 2
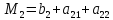
Превышает
величину
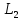 в силу наложенного условия
в силу наложенного условия
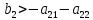
Наконец,
при
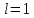 и выборе оператора
и выборе оператора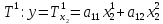
Игрок 1 обеспечивает себе выигрыш
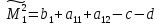
Выбором оптимальной стратегии
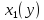 =
=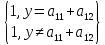
При этом игрок 2 опять получит строго больше своего МГР.
Заметим, что всегда
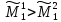
Более
того в линейной модели при любой
размерности
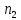 вектора
вектора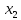 игроку 1 достаточно иметь всего лишь
один канал связи и ничего не потерять
в выигрыше!
игроку 1 достаточно иметь всего лишь
один канал связи и ничего не потерять
в выигрыше!
Определим условия на параметры модели, при которых
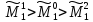
Используя выражения для оптимального выигрыша игрока 1 во всех этих случаях, имеем:
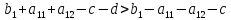
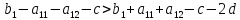
Из первого неравенства получим:
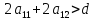
А
из второго
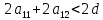
Окончательно имеем:
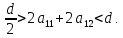
Задача. Подобрать численные значения параметров модели, при которых:
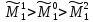

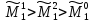
1
2
