Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

УМК

.PDF

Скачиваний:

102

Добавлен:

17.03.2015

Размер:

2.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 238 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

		0.3
		0.2
		0.1
		0
-2	-1	0	1	2	3	4	5	6
				Рис.1.15
		0.5
		0.4
		0.3
		0.2
		0.1
		0
-2	-1	0	1	2	3	4	5	6

Рис.1.16

Медианой MD случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е.

P(X < MD ) = P(X > MD ) .

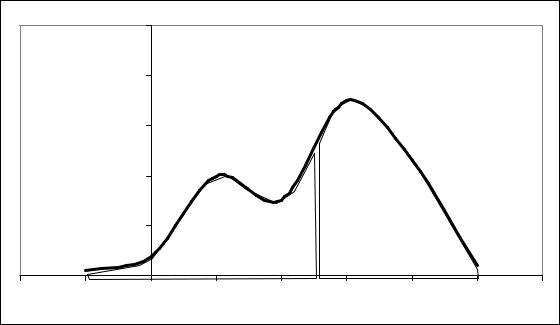
Геометрически медиана –				это абсцисса точки,			в которой площадь, огра-
ниченная кривой распределения, делится пополам (рис.1.17). Каждая из этих
площадей равна 0,5, т.к. вся площадь, ограниченная кривой распределения,
равна 1.
Поэтому		F(MD ) = P(X < MD ) = 0,5 .
		F(MD ) = P(X < MD ) = 0,5 .
Заметим, что если распределение одномодальное и симметрическое, то
все три характеристики положения случайной величины –								математическое
ожидание, мода и медиана –			совпадают.
		0.5
		0.4
		0.3
		0.2
		0.1
		0
-2	-1	0	1	2	D	3	4	5	6
					M
				Рис.1.17
		1.11. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

На практике при решении задач приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы нормального, показательного и равномерного распределений.

Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при достаточно часто встречающихся типичных условиях.

Примерами случайных величин, имеющих нормальное распределение, могут служить: отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров, ошибки при измерении, отклонения при

стрельбе и другие. Все эти примеры объединяет общая закономерность: случайная величина является результатом действия большого числа различных факторов, воздействие каждого из которых на данную величину незначительно и невозможно указать, какой именно влияет в большей степени, чем остальные.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

	1			−	( x − a ) 2
f ( x ) =			e		2	σ 2

						.
	σ 2	π

Очевидно, что нормальное распределение определяется двумя парамет-

рами: а и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание, σ - среднее квадратическое отклонение нормального распределения.

а) По определению математического ожидания непрерывной случайной величины

Выполним замену

x - a

= z,

(x−a)2

∞

e−

M(X) = ∫ x f (x)dx = ∫

2σ2 dx =

x = σz +a,

dx = σdz

σ 2π

−∞

при x →±∞

z →±∞

∞

∫ (σz + a) e−

σdz =

∫ z e−

dz +

∫e−

dz =

σ 2π

2π

−∞

∞

∫ z e−

dz = 0 как интеграл от нечетной функции

−∞

симметричными

пределами

интегрирования

= 0 + a = a.

относительно начала

координат,

∞

∫ e−

dz =

- интеграл

2π

Пуассона

−∞

Итак, М (X) = а, т. е. математическое ожидание нормального распределения равно параметру а;

б) По определению дисперсии непрерывной случайной величины, учитывая, что М(Х)=а, имеем

∞			∞		1		−	( x−a)2
D(X) = ∫	(x − M(X))	2	f (x)dx = ∫ (x − a)	2		e		2σ2


					σ 2π
−∞			−∞

dx =

Выполнимзамену

x - a

= z,

∞

x = σz + a,

dx = σdz

∫σ2z2e−

σdz =

∫z2 e−

dz =

σ 2π

2π

при x →±∞

z →±∞

−∞

z = u,

dz = du,

−

+ ∫e

−

∫z2 e 2 dz = ∫z e 2 zdz=

e 2 zdz= dv,

= −z e 2

2 dz

−

v= −e 2

=	σ 2

		2 π
		2 π
=	σ 2

		2 π
		2 π

Итак,


lim		−
lim		−
a → −∞
b → ∞

lim	−
b → ∞

z 2

∞

z 2

−

z e

2 dz

∫ e

− ∞

lim

2 π

= σ 2 .

b 2

a 2

→ −∞

D(X) = σ2 .

Следовательно,

σ(X) = D(X) = σ .

Таким образом, среднее квадратическое отклонение нормального рас-

пределения равно параметру σ.

Замечание. Общим называют нормальное распределение с произвольными параметрами а и σ (σ > 0).

Нормированным называют нормальное распределение с параметрами а=0

и σ =1.
1.11.1	Нормальная кривая
График плотности нормального распределения называют нормальной
кривой (кривой Гаусса). Исследуем функцию
	1			−	( x − a ) 2
y =					2 σ 2
				e
		σ
			2 π

методами дифференциального исчисления.

1.Очевидно, функция определена на всей оси x.

2.При всех значениях х функция принимает положительные значения, т.е. нормальная кривая расположена над осью Ох.

3Предел функции при неограниченном возрастании х (по абсолютной

величине) равен нулю:

lim	y = lim		1
lim	y = lim				( x − a )	2
x → ±∞	x → ±∞			e	( x − a )
		σ	2 π	e	2 σ 2

= 0

т.е ось Ох служит горизонтальной асимптотой графика.

4. Исследуем функцию на экстремум. Найдем первую производную:

y′

x − a

−

( x − a ) 2

= −

2 σ 2

2 π

Легко видеть, что

y ′

= 0

x = a

при

y ′

> 0

при x < a ,

y ′

< 0

при x > a .

Следовательно, при х=а функция имеет максимум, равный

y max

5. Исследуем функцию на точки перегиба. Найдем вторую производную:

−

( x − a ) 2

( x − a )

y ′ =

2 σ 2

− 1

2 π

Следовательно,

y′′

= 0 при x − a = ±σ

или

x = a ± σ

y ′

< 0

при x (a − σ, a + σ) ,

y′ > 0 при x ( −∞ , a − σ ) (a + σ, ∞ ) .

Таким образом, точки графика с абсциссами x = a ± σ являются точками перегиба.

6. Разность (х-а) содержится в аналитическом выражении функции в квадрате, т. е. график функции симметричен относительно прямой х=а.

На рис.1.18 изображена нормальная кривая при а==5 и σ =3.

	f(x)
	1
σ	2π
	a-σ	a	a+σ
		Рис.1.18
Выясним, как влияют на форму и расположение нормальной кривой зна-
чения параметров а и σ.
Известно, что графики функций f(х) и f(х-а) имеют одинаковую форму;
сдвинув график f (х) в положительном направлении оси х на а единиц масштаба
при а>0 или в отрицательном направлении при а<0, получим график f(х-а)
(рис.1.19).
	f(x)
-5	0	5	10	15	20	25
		M1(X)	M2(X) M3(X)
			Рис.1.19
Отсюда следует, что изменение величины математического ожидания не
изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси
Ох: вправо, если а возрастает, и влево, если а убывает.

По-иному обстоит дело, если изменяется параметр σ (среднее квадратическое отклонение). Как было показано ранее, максимум дифференциальной

функции нормального распределения равен σ 2π . Отсюда следует, что с воз-

растанием σ максимальная ордината нормальной кривой убывает, а сама кри- вая становится более пологой, т. е. сжимается к оси Ох; при убывании σ нор- мальная кривая становится более «островершинной», и растягивается в по- ложительном направлении оси Оу.

На рис.1.20 изображены нормальные кривые при различных значениях σ и а=0. Рисунок наглядно иллюстрирует, как изменение параметра σ сказывается на форме нормальной кривой.

f (x)
σ1 = 1
σ2 = 3
σ3	= 5
Рис.1.20
В случае, когда а=0 и σ =1, нормальную кривую называют нормирован-
ной. Подчеркнем, что при любых значениях параметров а и σ площадь, ограни-
ченная нормальной кривой и осью х, остается равной единице.

1.11.2. Вероятность попадания в заданный интервал нормальной случайной величины

Уже известно, что если случайная величина Х задана плотностью распределения f (x), то вероятность того, что Х примет значение, принадлежащее интервалу (α;β) , такова:

P(α < X < β) = ∫f (x)dx

Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу (α;β) , равна

		1		β	−	( x −a )2
P(α < X < β) =				∫ e
						2 σ2
						2 σ2
	σ			α
	σ		2π	α

dx .

Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами.

Выполним замену

x − a

= z,

β −

( x −a )

P (α < X < β) =

dx =

∫ e

2 σ 2

x = σz + a, dx = σdz

2π

при

x = α

z =

α - a

при x = β

z = β - a

β-a

∫

e−

σdz =

∫e−

σdz +

∫ e−

σdz =

σ 2π

2π

-a

2π -a

β-a

α-a

∫ e−

σdz −

∫ e−

σdz.

2π

Пользуясь функцией Лапласа

−

z 2

Ф ( x ) =

∫ e

dz ,

2 π

окончательно получим

β - a

α - a

P(α < X < β) = Ф

− Ф

σ .

Пример 1.46 Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10;50).

Решение. По условию, α=10, β=50, a=30, σ=10, следовательно,

	50 - 30		10 - 30
P(10 < X < 50) = Ф		− Ф		= 2Ф(2) .
	10		10

По таблице находим Ф(2)=0,4772. Отсюда искомая вероятность

P (10 < X < 50 ) = 2 0 , 4772 = 0 ,9544 .

1.11.3. Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х по абсолютной величине меньше заданного положительного числа δ, т. е. требуется найти вероятность осуществления неравенства

X − a < δ .

Заменим это неравенство равносильным ему двойным неравенством

− δ < X − a < δ

или

a − δ < X < a + δ .

Далее
a + δ - a		a − δ - a
P(a − δ < X < a + δ) = Ф		− Ф		=
	σ		σ

δ .

= Ф

− Ф

−

= −Ф

= 2Ф

Итак

X − a

< δ) = 2Ф

В частности, при а=0
			δ

P(	X	< δ) = 2Ф		.

			σ

На рис.1.21 наглядно показано, что если две случайные величины нормально распределены и а=0, то вероятность принять значение, принадлежащее интервалу (-δ;δ), больше у той величины, которая имеет меньшее значение σ. Данное обстоятельство полностью отражает вероятностный смысл параметра σ, т.к. σ характеризует рассеяние случайной величины вокруг ее математического ожидания.

f (x)
σ1	= 1
	σ2	= 3
Рис.1.21
1.11.4. Правило трех сигм

Преобразуем формулу

			δ

P(	X − a	< δ) = 2Ф		,

			σ

положив

δ = σ t .

В итоге получим

P(X − a < σt ) = 2Ф(t ).

Если t=3, то

P(X − a < 3σ) = 2Ф(3) = 2 0,49865 = 0,9973 ,

т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсо- лютная величина ее отклонения от математического ожидания не превосхо- дит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном

<<< < Предыдущая 1 2 3 4 5 6 78 / 238 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.05.2019378.37 Кб3УМК по дисциплине Римское право.doc
#
17.03.2015683.52 Кб13УМК по КП. бак 30.10.2012.doc
#
19.09.2019195.07 Кб2УМК-КУ ПОЭ.doc
#
17.03.2015661.5 Кб75УМК.doc
#
17.03.20151.66 Mб62УМК.PDF
#
17.03.20152.52 Mб102УМК.PDF
#
17.03.20153.93 Mб91УМК.PDF
#
17.03.20151.09 Mб47УМК.PDF
#
17.03.20152.61 Mб46УМК.PDF
#
17.03.20151.65 Mб20УМК11.pdf
#
17.03.20151.57 Mб136УМК6.pdf