УМК6

СОДЕРЖАНИЕ

1. Теоретические основы

1.1

Первообразная функция и неопределенный интеграл

7

1.2

Простейшие свойства неопределенного интеграла и его геометрический

8

смысл

1.3

Таблица основных интегралов

10

1.4

Основные методы интегрирования

11

1.4.1 Интегрирование методом разложения

11

1.4.2 Интегрирование методом замены переменной

12

1.4.3 Метод интегрирования по частям

17

1.5

Интегрирование дробно - рациональной функции

20

1.5.1 Некоторые сведения о многочленах

20

1.5.2 Виды рациональных дробей

22

1.5.3 Разложение правильной рациональной дроби

23

на сумму простейших дробей

25

1.5.4 Интегрирование простейших дробей

1.5.5 Общий план интегрирования дробно - рациональной функции

29

1.6

Интегрирование некоторых классов тригонометрических функций

31

1.6.1 Рациональная функция двух независимых переменных

31

1.6.2 Интегралы вида ∫R(sin x, cos x)dx

31

1.6.3 Частные методы вычисления интегралов ∫R(sin x, cos x)dx

33

1.7

Интегрирование некоторых классов иррациональных функций

36

1.8

Задача, приводящая к понятию определенного интеграла

40

1.9

Определение определенного интеграла

41

1.10 Свойства определенного интеграла

43

1.11 Определенный интеграл с переменным верхним пределом

46

интегрирования

1.12 Формула Ньютона-Лейбница

48

1.13 Замена переменной в определенном интеграле

49

1.14 Интегрирование по частям в определенном интеграле

50

1.15 Несобственные интегралы

51

1.15.1 Несобственные интегралы с бесконечными пределами

51

интегрирования

1.15.2 Несобственные интегралы от неограниченных функций

54

1.16 Геометрические приложения определенного интеграла

55

1.16.1 Вычисление площади в декартовых координатах

55

1.16.2 Площадь криволинейного сектора

58

1.16.3 Длина дуги плоской кривой

61

1.16.4 Объем тела вращения

63

1.17 Применение определенных интегралов к решению некоторых задач

65

механики и физики

1.17.1 Схема применения определенного интеграла

65

1.17.2 Работа переменной силы

66

1.17.3 Статистические моменты. Координаты центра тяжести системы

68

материальных точек

1.17.4 Центр тяжести плоской линии

69

2. Методические указания для студентов

2.1

Непосредственное интегрирование

72

2.1.1 Основные определения

72

2.1.2 Свойства неопределенного интеграла

72

2.1.3 Таблица неопределенных интегралов

72

2.1.4 Метод непосредственного интегрирования

73

2.2

Инвариантность формул интегрирования. Методы интегрирования

76

2.2.1 Метод введения функции под знак дифференциала

76

2.2.2 Интегрирование методом подстановки

80

2.3

Интегрирование функций, содержащих квадратный трехчлен

82

2.4

Интегрирование по частям

86

2.5

Интегрирование рациональных функций

89

2.5.1 Интегрирование простейших дробей

89

2.5.2 Разложение правильной рациональной дроби на сумму

простейших дробей. Интегрирование рациональных дробей

93

2.6

Интегрирование тригонометрических функций

98

2.6.1 Интегралы от функций sin mx cosnx , cos mx cos nx , sin mx sin nx

98

2.6.2 Интегралы от функций sinn x, cosn x

99

100

2.6.3 Интегралы от функций sinm x cosm x (m, n – целые числа)

102

2.6.4 Интегралы от функций sinm x cosm x (m, n – целые числа)

2.7

Интегрирование иррациональных функций

105

2.7.1 Сведение иррациональных функций к рациональным

105

2.7.2 Сведение иррациональных функций к тригонометрическим

107

2.7.3 Интегрирование дифференциальных биномов

110

2.8

Определенный интеграл

114

2.8.1 Вычисление определенного интеграла

115

2.9

Несобственные интегралы

120

2.9.1 Интегралы с бесконечными пределами интегрирования

120

2.9.2 Интеграл от неограниченных функций

123

2.10 Геометрические приложения определенного интеграла

127

2.10.1 Вычисление площади плоской фигуры

127

2.10.2 Вычисление длины дуги кривой

134

2.10.3 Вычисление координат центра тяжести

138

2.10.4 Вычисление объема тела вращения

142

2.10.5 Вычисление площади поверхности вращения

145

2.11 Применение определенного интеграла к решению некоторых задач

146

физики

146

2.11.1 Вычисление работы

2.11.2 Давление жидкости

148

2.11.3 Истечение жидкости из емкости

150

3. Материалы для самостоятельной работы студентов

3.1. Контрольные вопросы

153

3.2. Задачи и упражнения для самостоятельной работы

154

3.3. Расчетные задания

168

3.4. Лабораторная работа

198

3.5. Литература

202

функции f (x)

на некотором промежутке, если

в каждой точке этого

промежутка

F (x) = f (x)

(1.1)

′

или, что тоже,

dF(x) = f (x)dx

(1.2)

Например,

F(x) = sin x является первообразной для f (x) = cos x на всей

′

′

′

′

= f (x) для любого числа C R . Тогда,

F (x) = f (x), то

(F(x) +C)

= F (x) +C

согласно (6.1), F(x) +C есть первообразная для f (x) .

Например,

если f (x) = 4x3 ,

то

функции

F (x) = x4 ,

F (x) = x4 +1,

F (x) = x4 −2 и

F(x) = x4 +C , где

1

2

вообще

C

любое

число, будут

3

дается следующей теоремой.

Теорема 1.1 Если функция F(x) есть первообразная для функции f (x)

на [a; b], то всякая другая первообразная для f (x) отличается от F(x)

на

постоянное слагаемое, то есть может быть представлена в виде F(x) +С,

где

С постоянная.

Доказательство. Пусть Φ(x) любая другая первообразная для функции

f (x) ,

′

′

тогда Φ (x) = f (x) = F (x) . Пусть ϕ(x) = Φ(x) −F(x) на [a; b]. Тогда

′

′

′

ϕ (x)

= Φ (x) −F (x) = 0. Следовательно, функция ϕ(x) постоянна на [a;b], то

7

где C некоторое число. Теорема 1.1 доказана.

F(x) +С

Из теоремы 1.1 следует, что выражение

охватывает всю

совокупность первообразных для данной функции f (x) .

ОПРЕДЕЛЕНИЕ 1.2 Если F(x) одна из первообразных для функции

f (x) на [a; b], то выражение F(x) +С,

где

C

произвольная

постоянная,

называется неопределенным интегралом

от

функции f (x)

и

обозначается

∫f (x)dx = F(x) +C

,

(1.3)

где f (x) называется подынтегральной

функцией,

f (x)dx

-

подынтегральным выражением, x - переменной интегрирования, а символ ∫

-

знаком неопределенного интеграла.

достаточно продифференцировать

результат

интегрирования

F(x) +C и

сверить его с заданной функцией f (x) . Если (F(x) +C)

будет равна f (x) , то

′

интегрирование осуществлено верно.

Например, ∫

dx

=

1

arctg

x

+C , так

x2 +

4

2

как

2

′

1

x

=

1

1

1

=

1

arctg

+C

2

2

2

x

2

2

4 + x2

1+

2

′

(∫f (x)dx)′ = f (x) .

(1.4)

= f (x) и согласно (1.3) ∫f (x)dx = F(x) +C . Тогда

Действительно, F (x)

′

′

′

(∫f (x)dx)

= (F(x) +C)

= F (x) = f (x).

20

Дифференциал

от

неопределенного

интеграла

равен

подынтегральному выражению

d(∫f (x)dx)= f (x)dx .

(1.5)

8

∫F′(x)dx = F(x) +C.

(1.6)

Действительно,

F′(x) = f (x).

Тогда,

∫F′(x)dx = ∫f (x)dx = F(x) +C

согласно определения 1.2.

40

Неопределенный

интеграл

от

дифференциала

равен

дифференцируемой функции плюс произвольная постоянная:

∫dF(x) = F(x) +C .

(1.7)

Действительно, dF(x) = f (x)dx . Тогда,

∫dF(x) = ∫f (x)dx = F(x) +C.

50

Постоянный

множитель

k (k ≠ 0)

можно выносить

за знак

неопределенного интеграла:

∫k f (x)dx = k ∫f (x)dx .

(1.8)

функции равен алгебраической сумме интегралов от этих функций:

∫[f1(x) + f2 (x) +... + fk (x)]dx =

(1.9)

= ∫f1(x)dx + ∫f2 (x)dx +... + ∫fk (x)dx

Доказательство. Дифференцируя левую часть (1.9), получим

(∫[f1(x) +f2 (x) +... +fk (x)]dx)′ = f1(x) +f2 (x) +...+fk (x) .

Дифференцируя правую часть (1.9), получим

′

′

+

(∫f1(x)dx + ∫f2 (x)dx +...+ ∫fk (x)dx) = (∫f1(x)dx)

y

Так как производные равны,

то

равенство (1.9) справедливо с точностью до

постоянного слагаемого.

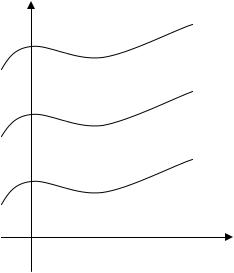
y = F(x) +C3

Выясним

геометрический

смысл

неопределенного интеграла.

Пусть функция

y = F(x)

является

y = F(x) +C2

первообразной

для

функции

f (x) .

Назовем

график первообразной

F(x)

интегральной

кривой. График любой другой первообразной

y = F(x) +C1

y = F(x) +C

при

любом

постоянном

С

x

может

быть

получен

параллельным

0

Рис. 1.1

переносом

интегральной

кривой

y = F(x)

вдоль

оси

Oy .

Следовательно,

1

∫xαdx =

xα+1

+C , α R , α ≠ −1

(1.10)

dx

α+1

2

∫

= ln

x

+ C

(1.11)

x

3

∫dx = x +C

(1.12)

4

∫

аxdx =

ax

+C, a > 0, a ≠1

(1.13)

ln a

5

∫exdx = ex +C

(1.14)

6

∫sin x dx = −cos x +C

(1.15)

7

∫cos x dx = sin x +C

(1.16)

8

∫

dx

= −ctg x +C

(1.17)

sin2

x

9

∫

dx

= tg x + C

(1.18)

cos2

x

10