Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

“УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ”

Кафедра вычислительной техники и инженерной кибернетики

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ

Учебно – методическое пособие по выполнению

лабораторной работы по программированию

Уфа 2008

Методическое пособие предназначено как для студентов специальности 220400 “Программное обеспечение вычислительной техники и автоматизированных систем” для изучения дисциплины “Программирование на языке высокого уровня”, так и для других технических специальностей по информатике или основам программирования.

Составители: Белозеров Е.С., доц.

Рецензент Иванов В.И., доц., канд. техн. наук

© Уфимский государственный нефтяной технический университет, 200 8

1. Цель работы

1. Закрепление навыков алгоритмизации и программирования с применением подпрограмм-функций.

2. Освоение навыков создания новых типов данных с помощью оператора typedef.

3. Передача сложных типов данных через механизм формальных/фактических параметров.

4. Знакомство с простейшими методами численного интегрирования функций.

2 Алгоритмы численного интегрирования функций

Определенный интеграл от функции f(x) легко вычисляется по формуле Ньютона-Лейбница

, (1)

если мы располагаем аналитической формулой её первообразной F(x).

Однако при решении практических и экспериментальных задач очень редко удаётся выразить F(x) через элементарные функции и поэтому приходится искать интеграл I приближенными численными методами с помощью квадратурных формул, то есть путем вычисления площадей.

Простейшими методами численного интегрирования являются метод прямоугольников, трапеций и парабол (Симпсона). Рассмотрим их алгоритмы.

В методе прямоугольников значение интеграла (т.е. площади криволинейной трапеции) на интервале (a, b) заменяется суммой площадей прямоугольников в соответствии с рисунком

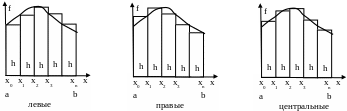
Рисунок 1 Способы построения прямоугольников

где h - шаг интегрирования, расстояние между узлами x₀, x₁, x₂, x₃, ....

Каждый прямоугольник имеет высоту f(x_i) и ширину h =(b-a)/n и поэтому расчетная формула очень проста

, (2)

Кстати, она вытекает из определения понятия интеграла, как предела интегральной суммы при устремлении числа отрезков n к бесконечности.

Приведенные на рисунке 1 варианты построения прямоугольников (левые, правые и центральные) различаются точностью вычисления I_п (при одинаковом n).

Разработаем универсальный алгоритм вычисления приближенного вычисления интеграла I_п.

Из формулы (2) очевидно, что надо в цикле меняя x от a до b с шагом h надо вычислять f(x) и накапливать сумму S по известному рекуррентному алгоритму

S = S +f(x),

Заодно можно накапливать и текущее значение аргумента x = x +h.

Для этого вначале ячейку S надо обнулить, S=0, и установить начальное значение x по универсальной формуле (годящейся трех вариантов)

x = a + c * h (3)

где c - смещение первого узла x₀ относительно нижнего предела a,

при c = 0 будут левые прямоугольники, c = 1 - правые, а при c = 0.5 центральные.

Таким образом, схема алгоритма вычисления интеграла (2) будет иметь вид.

Рисунок 2 Алгоритм вычисления интеграла методом прямоугольников

Как хорошо видно на рисунке 1 центральные прямоугольники более плотно прилегают к нашей функции f(x), а погрешности левой и правой частей каждого прямоугольника взаимно компенсируются. Поэтому центральные прямоугольники работают значительно точнее.

В методе парабол используют полученную Симпсоном квадратурную формулу, согласно которой криволинейная трапеция на участке из трех узлов x₀, x₁, x₂. заменяется площадью параболы (см. рисунок 3).

S = ( f(x₀) + 4 f(x₁) +f(x₂) )*h/3 (4)

С

Рисунок 3

уммируя все параболы на интервале (a, b) с шагом h получаем формулу приближенного значения интеграла

(5)

Нечетные ординаты имеют коэффициент 4 согласно формуле Симпсона, а у четных - коэффициент 2, поскольку они учитываются дважды у левой параболы и у правой. Неудобство формулы (5) в том, что число четных (внутренних) ординат, с учетом коэффициента 2 на 2 штуки меньше чем нечетных. Для упрощения алгоритма надо выровнять суммы для реализации расчетов в одном цикле. Тогда вторая сумма учтет две лишних ординаты f_n = f_b , поэтому их надо отнять. В результате получим

(5')

Принимая как в предыдущем методе шаг интегрирования h =(b-a)/n, организуем цикл по параболам, изменяя номер i от 1 до m = n/2 и аргумент x с шагом 2 h.

При этом, вместо обнуления ячейки S, запишем вначале туда разность крайних ординат

S= f_a - f_b

а в качестве начального значения аргумента x примем узел x₁ , т.е.

x = a +h

Сумму S согласно (5') накапливаем по формуле

S = S + 4f(x) +2 f(x+h).

Таким образом, получаем схему алгоритма вычисления интеграла методом Симпсона (рисунок 5).

В результате из формул (2) и (5) мы получили компактные и удобные алгоритмы численного интегрирования при заданном числе шагов n. Проблема в том, что мы не знаем заранее, как выбрать приемлемое число шагов интегрирования n . При одних n точность будет хорошая при другом не очень, всё зависит от свойств интегрируемой функции.

С другой стороны мы всегда можем назначить подходящее значение точности (или погрешности расчетов). Для этого надо уметь оценивать точность расчетов и разработать алгоритм, который бы сам останавливался по достижению заданной точности.

3 Оценка погрешностей методов

Абсолютной погрешностью называют разность между истинным x_и и приближённым x_П значением измеряемой (вычисляемой) величины

_а = | x_и - x_п |, (6)

модуль берут исключительно для удобства.

К сожалению, абсолютная погрешность зависит от самой измеряемой величины, поэтому на практике используют относительную (относительно самой измеряемой величины) погрешность

, (7)

которая не зависит от самой измеряемой величины x.

Для наших расчетов, в принципе можно пользоваться любой погрешностью _а или _от..

Для рассмотренных методов численного интегрирования известны теоретические формулы для оценки погрешности каждого метода, которые сведены в таблице 1.

Таблица 1. Погрешности методов численного интегрирования (8)

1	метод левых и правых прямоугольников
2	метод центральных прямоугольников
3	метод трапеций
4	метод парабол (Симпсона)

где ξ- такой x, при котором производные максимальны.

К сожалению, пользоваться формулами теоретической погрешности для остановки алгоритмов мы не можем, т.к. они зависят производных и надо решать экстремальную задачу, что значительно сложнее, чем само интегрирование. Формулы из табл. 1 позволяют нам только сравнивать и оценивать алгоритмы, что само по себе весьма существенно.

Например, формула 1 для правых прямоугольников, говорит нам, что погрешность (точность) метода пропорциональна шагу интегрирования h и значению первой производной f(x).

Метод центральных прямоугольников обеспечивает точность пропорциональную квадрату шага h и значению второй производной f"(x), а метод Симпсона - четвертой степени h и значению четвертой производной - f^IV(x).

Это означает, что метод левых прямоугольников дает нулевую погрешность для линейной функции f(x) = a+ bx, метод центральных прямоугольников для квадратичной функции f(x) = a+ bx + c x², а метод Симпсона даст нулевую погрешность для кубической параболы.

Кроме того, трактовка формул (8) позволяют нам судить об эффективности разных методов. Формулы (8) говорят нам, что при уменьшении шага в два раза погрешность расчетов по методу левых прямоугольников должна уменьшиться в два раза (что не очень здорово), по методу центральных прямоугольников - в четыре раза, а по методу Симпсона - аж - в 2⁴ =16 раз. В этом студент сможет убедиться в своих программах.

Проблема получения алгоритма численного интегрирования по заданной точности (погрешности) остаётся.

Для этого можно воспользоваться традиционным методом проб и ошибок или принципом двойного просчета.