8. Свойства сочетаний

Отметим некоторые свойства сочетаний:

1. (свойство симметрии).

Например,

2. (свойство Паскаля).

Данное равенство является рекуррентным соотношением для числа сочетаний. С помощью этого равенства можно составить таблицу для нахождения числа сочетаний. Расположим сочетания в виде треугольной таблицы

П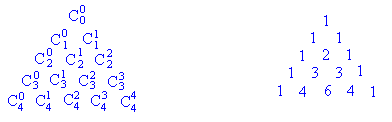олученную треугольную таблицу принято называтьтреугольником Паскаля.

3. .

Пример 8.1. Решить уравнение

.

Решение. Поскольку , то получим квадратное уравнение

.

Учитывая, что , получаем решение

.

Пример 8.2. Решить неравенство

.

Решение. Из условия задачи следует, что n2 и n. Поскольку

, ,

то

.

Таким образом, исходное неравенство равносильно неравенству

.

Поскольку при n=10 получаем , а приn=9 получаем . Учитывая, чтоn2 получаем

.

Пример 8.3. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков?

Решение. Для звукосочетания клавиши нажимаются одновременно, поэтому для k звуков имеем звукосочетаний. Таким образом, искомое количество есть

.

Учитывая свойство 3, т.е., что

,

получим

.

Упражнения

8.1. Вычислить: а) , б) .

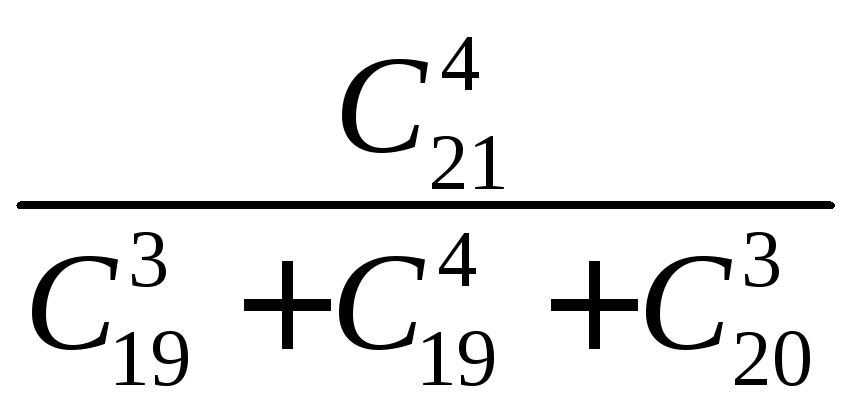Ответ: а) 81, б) 1.

8.2. Упростить: .

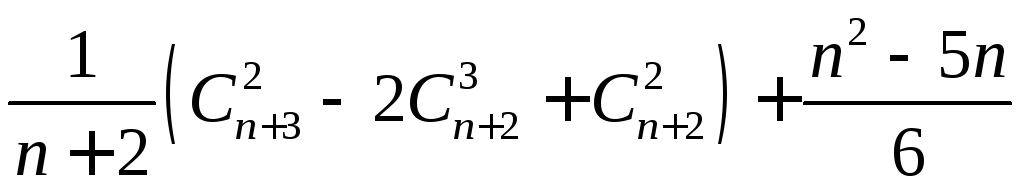Ответ: 2.

8.3. Найти все натуральные n, удовлетворяющие условию:

а) , б).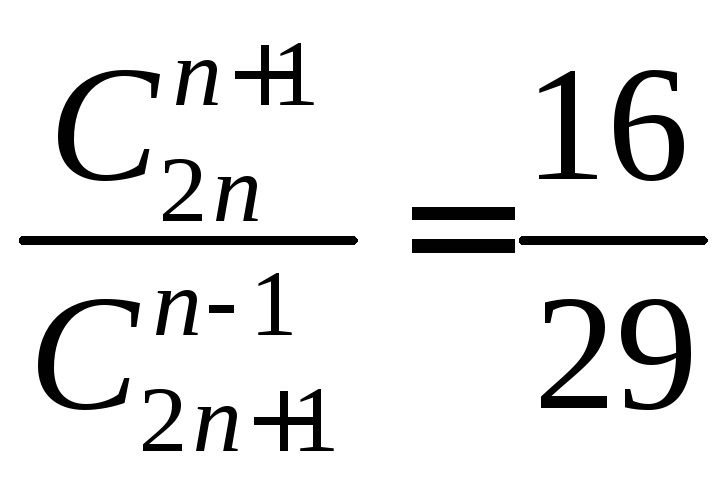

Ответ: а) 3, б) 14.

8.4. Решить неравенство: а) , б).

Ответ: а) , б),

8.5. Доказать, что .

8.6. Имеется 12 различных цветов. Сколькими способами можно составить букет из данных цветов, если в букет должно входить не менее 3 цветов?

Ответ: .

9. Свойства биномиальных коэффициентов

Свойство 3 является следствием формулы бинома Ньютона:

. (9.1)

Поэтому сочетания еще иногда называют биномиальными коэффициентами.

Сумма биномиальных коэффициентов всех членов разложения равна 2ⁿ. Сумма биномиальных коэффициентов членов разложения, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах, и равно 2^n–1.

Пример 9.1. Найти разложение степени бинома (2x–3)⁵.

Решение. Полагая a=2x, b=–3, получим

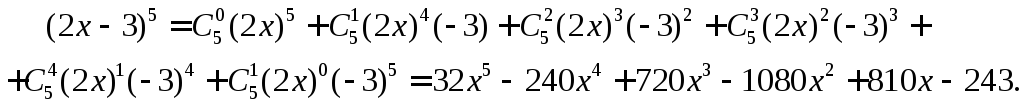
Пример 9.2. Пятый член разложения 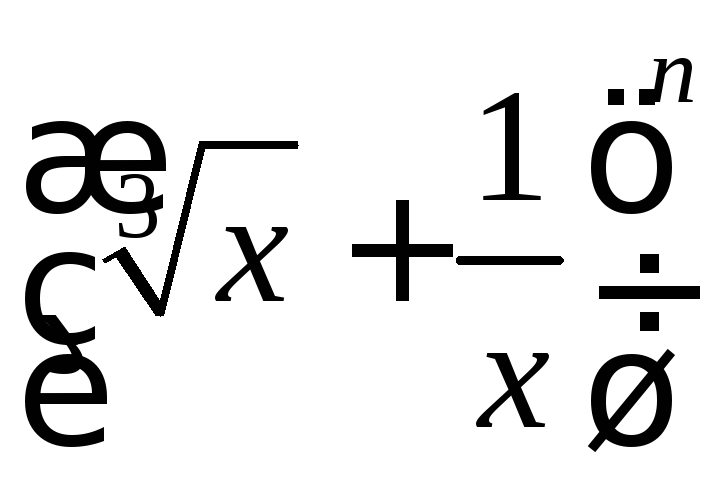не зависит отx. Найти n.

Решение. Пятый член разложения T₅ имеет следующий вид:

.

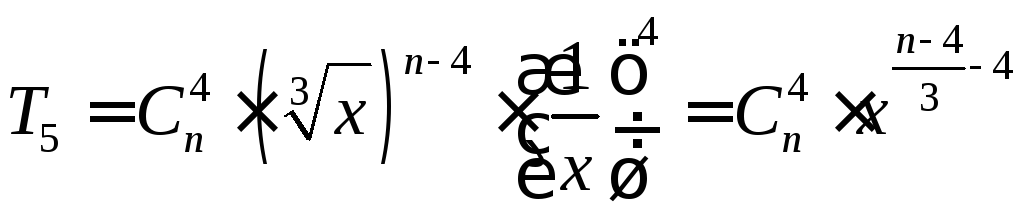По условию T₅не зависит отx; это означает, что показатель степени приxравен нулю, т.е. (n–4)/3–4=0. Из последнего уравнения находимn=16.

Пример 9.3. Вычислить сумму

.

Решение. Согласно формуле бинома Ньютона, при любом x имеем равенство:

.

Полагая здесь x=1, получим

.

Итак, искомая сумма равна 3⁵, т.е. 243.

Упражнения

9.1. Напишите разложение степени бинома

а) ;б) ;в) .

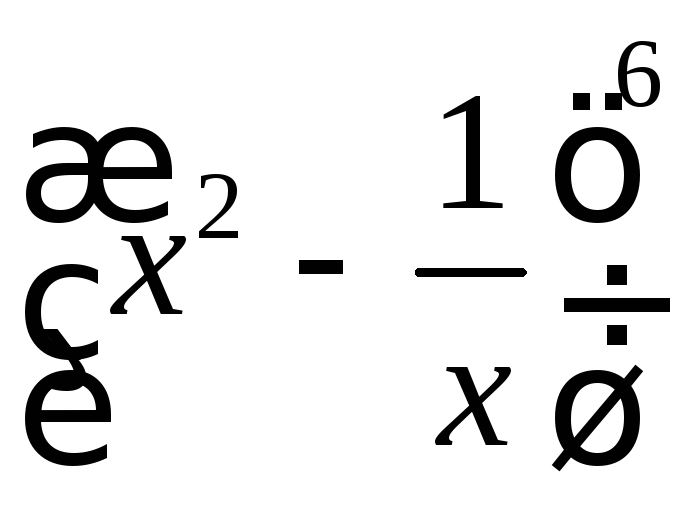Ответ: а) ,

б) ,

в) .

9.2. Найдите пятый член разложения .

Ответ: .

9.3. Найдите два средних члена разложения .

Ответ: и.

9.4. Найдите в биномиальном разложении 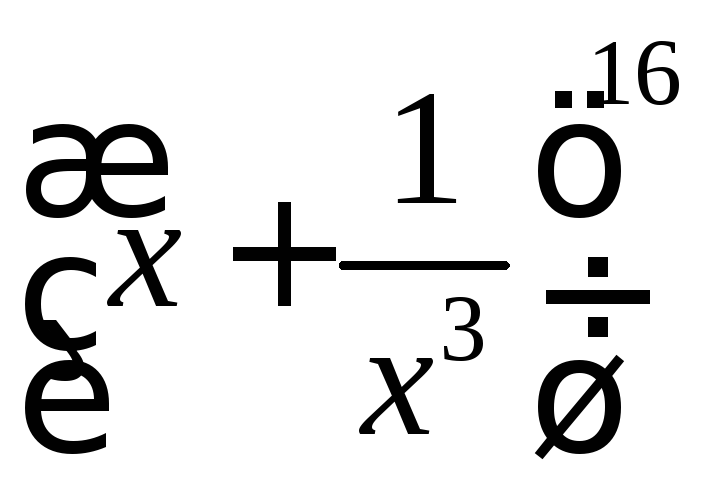член, не содержащийx.

Ответ: .

9.5. Найдите сумму .

Ответ: .

9.6. Сумма биномиальных коэффициентов разложения 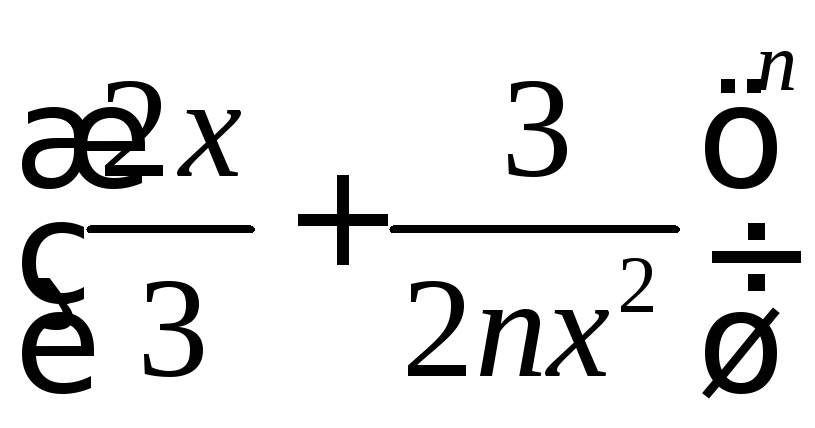равна 64. Напишите член, не содержащий переменнуюx.

Ответ: n=6, .

10. Размещения с повторениями

Пусть выбор k элементов из некоторого множества, состоящего из n элементов, производится с возвращением и с упорядочением их в последовательную цепочку. Различными исходами такого выбора будут всевозможные наборы (вообще говоря, с повторениями) отличающиеся либо составом элементов, либо порядком их следования. Получаемые в результате комбинации называются размещениями с повторениями из n элементов по k элементов.

Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента: ab, ac, ba, bc, ca, cb, aa, bb, cc.

Таким образом, размещение с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т.е. каждое размещение с повторениями из n элементов по k элементов может состоять не только из различных элементов, но и k каких угодно и как угодно повторяющихся элементов.

Число размещений с повторениями можно найти из принципа умножения. Первый элемент размещения можно выбратьn способами. Второй элемент также можно выбрать n способами (ведь элементы могут повторяться) и т.д. По принципу умножения находим

. (10.1)

Пример 10.1. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?

Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т.е. набор упорядоченный), причем возможны повторения (т.е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:

Пример 10.2. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?

Решение. Данная задача есть задача на отыскание числа размещений с повторениями

.

Пример 10.3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?

Решение. Число всех букв, каждая из которых записывается одним символом, равно .

Число всех букв, каждая из которых записывается двумя символами, равно .

Число всех букв, каждая из которых записывается тремя символами, равно .

Число всех букв, каждая из которых записывается четырьмя символами, равно .

Число всех букв, каждая из которых записывается пятью символами, равно .

Число всех указанных букв будет равно 62.

Упражнения

10.1. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?

Ответ: .

10.2. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?

Ответ: .

10.3. Сколькими способами можно разместить 8 пассажиров по трем вагонам?

Ответ: .

10.4. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?

Ответ: .

10.5. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа (повторение цифр разрешается). Сколько среди них чисел, у которых: 1)a=1; 2) a2; 3) a=3, b=2; 4) a=3, b=4, c=5?

Ответ: .

10.6. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?

Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2^k k-значных числа, то общее количество искомых чисел равно . б) Для трёх цифр аналогично получаем . в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим чисел.

10.7. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?

Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 2³ способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т.е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше: способов выбора кур. Точно так же естьспособов выбора уток испособов выбора гусей. Всегоспособов.