Неорганическая химия / Астахов М.В. Теория химической связи

Более удобна для расчетов формула, предложенная Капустинским. Он показал, что

где Σm — число ионов в формуле соединения; k — постоянная ≈ 0,87. Принимая равновесное расстояние между ионами в кристалле равным сумме радиусов катиона (rK) и аниона (rА), вместо уравнения 49б, он получил

Если подставим значения NA, k, e и ρ, равное 0,345•10-10 метра, в (65а), получим

Для кристаллической решетки, содержащей ионы с различным зарядом (Z1 и Z2), это уравнение записывается следующим образом

где Uреш - энергия ионной решетки, кДж/моль;

rK и rА - кристаллохимические радиусы Гольдшмидта для координационного числа 6. Из формул Борна (48) и Капустинского (65) следует, что наиболее стабильны решетки,

образованные небольшими и сильно заряжёнными ионами. Эти уравнения применяются для расчета неизвестных теплоты образования кристаллов, теплоты сольватации и т. п. Однако чем сильнее отличается полярная связь в кристалле от идеализированной ионной, тем менее точные результаты дают формулы Борна и Капустинского.

31

3.Ковалентная связь.

Электростатическая модель, на основе которой достаточно просто можно объяснить образование молекул из атомов, оказалась абсолютно непригодной для понимания образования даже таких простых молекул, как Н2, О2 и т.д., не говоря о более сложных молекул. Для расчета энергии связи и структуры сложных молекул требуется квантомеханический подход, который был развит для атомов на основании уравнения Шредингера. Точное решение этого уравнения возможно только для одноэлектронной системы, для более сложных многоэлектронных систем, какими являются многоэлектронные атомы и молекулы, были развиты приближенные методы расчета такие как метод возмущений и вариационный метод.

Вариационный метод, подробно изложенный в приложение 4, дает возможность приблизительного определения энергии системы, но для этого необходимо подобрать правильную волновую функцию, что не всегда легко сделать. Для вычисления энергии молекулы используются два метода, основанных либо на теории молекулярных орбиталей, либо на теории валентных связей. Эти две теории подходят к построению исходной волновой функции совершенно различными путями, а также отражают разные представления об основной модели строения молекулы. Теория валентных связей была разработана на много лет раньше теории молекулярных орбиталей. Она дает более наглядное представление о строении молекулы, и поэтому ее чаще применяют для качественного решения некоторых вопросов. Однако в последние годы теория молекулярных орбиталей стала наиболее популярной, что можно объяснить большей простотой этой теории и используемого математического аппарата.

В то время как теория валентных связей сохраняет за атомами, входящими в состав молекулы, их индивидуальность, теория молекулярных орбиталей рассматривает молекулу как единую частицу на основе идей, которые были использованы при рассмотрении строения многоэлектронных атомов.

3.1 Молекулярный ион водорода.

Рассмотрим простейшую возможную двухядерную частицу — молекулярный ион водорода Н+2. Предполагают, что ядра находятся бесконечно далеко одно от другого, что эквивалентно системе

Н+ Н+

(а) (b)

Пусть электрон находится у атома а, и основное состояние такой системы будет выражено с помощью атомарной орбитали ψa =ψ1sb . Теперь примем, что электрон находится у атома b, тогда основное состояние системы можно будет описать атомарной орбиталью

ψb =ψ1sb , что указывает на связь электрона только с атомом b. Если ядра будут сближаться, то образующую новую систему можно описать суммой двух этих состояний,

32

поскольку каждая из них является решением уравнения Шредингера. Для определения основного энергетического состояния такой молекулы в нулевом приближении можно построить предполагаемую волновую функцию как линейную комбинацию 1s орбиталей атомов водорода.

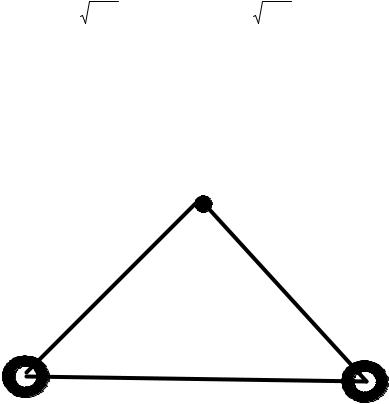
Пользуясь обозначениями рис. 10, получим оператор Гамильтона для молекулярного иона водорода

e

Рис. 10. Координаты для электрона в молекулярном ионе водорода

Уравнение Шредингера для молекулы иона водорода будет иметь следующий вид:

Используя стандартный метод решения уравнения Шредингера, умножим правую и левую часть уравнения (68) на Ψ1 (66) и проинтегрировав его по всей области изменения переменных, получим выражение для энергии:

Для нахождения энергии системы обычно применяют вариационный метод, с помощью которого находят минимум энергии рассматриваемой системы. (Приложение 4). В нашем случае параметрами, которые позволяют минимизировать энергию, являются коэффициенты С1 и С2 при атомарных волновых функциях ψa и ψb.

33

Действуя оператором на волновую функцию (66), получим несколько интегралов, которые обозначим следующим образом:

Два последних интеграла равны единицы, поскольку ψа и ψа нормированные функции (67а). Достаточно просто показать, что интегралы Hab и Hab равны между собой

Первые два члена в скобках являются решением уравнения Шредингера для атома водорода, в данном случае атома в, т.е.

Аналогичные преобразования можно сделать и для интеграла Нba, что позволит записать его следующим образом:

А используя введенные ранее обозначения интегралов, еще в более компактной форме:

34

Аналогичное уравнение получатся после дифференцирования уравнения (74б) по С2:

Преобразуя их относительно двух вирируемых параметров С1 и С2 и учитывая, что Saa=Sbb=1 и обозначив Sab = Sba=S, получим систему двух уравнений относительно этих коэффициентов:

С1(Нba-ЕS)+С2(Hbb-E)=0

Используя стандартное решение системы двух линейных уравнений, получим опреде-

литель второго порядка, который называют вековым:

В случае иона молекулы водорода ядра а и b совершенно «равноправны», так что Наа=Hbb Тогда уравнение (81) будет иметь следующий вид:

Энергия молекулы Hab, соответствующую минимуму энергии системы, поскольку интегралы Нaa и Hab отрицательны, называют энергией симметричного состояния и помечают

35

индексом «с» Е1≡Ес, а Е2 соответствует антисимметричному Е2≡Еас Каждой из этих энергий соответствует своя молекулярная орбиталь.

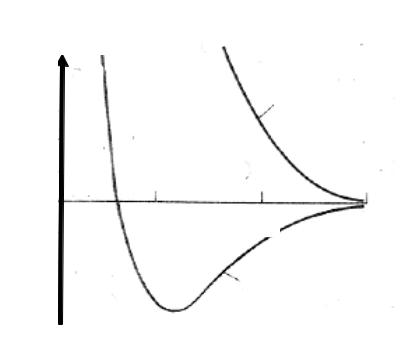
Результат расчета зависимости энергии для иона молекулы водорода в зависимости от расстояния между ядрами приведены на рис. 11.

Е

40

Eас

20

0

-20

Ec

-40

Рис. 11. Кривые потенциальной энергии молекулярного иона водорода для симметричного (Eс) и антисимметричного (Еас) энергетических состоянии.

Антисимметричное состояние соответствует неустойчивому энергетическому состоянию молекулы, и, переход электрона на антисимметричную орбиталь приведет к развалу молекулы, поскольку энергия разъеденных частиц будет меньше, чем в этой молекуле. С другой стороны, симметричное энергетическое состояние ведет к минимуму потенциальной энергии и поэтому к образованию устойчивой частицы.

Посредством выбранной волновой функции была вычислена наименьшая потенциальная энергия, соответствующая энергии диссоциации, она равна 1,76 эВ. Было вычислено, что равновесное расстояние между ядрами равно 1,32 Ǻ. На опыте найдено, что энергия диссоциации равна 2,791эв, а равновесное расстояние — 1,06 Ǻ. Таким образом, расчеты показывают, что молекулярный ион водорода — устойчивая частица, но они показывают также, что принятая волновая функция должна быть исправлена.

Наряду с энергетическими состояниями интересно распределение электрона в молекулярном ионе водорода, как в симметричном, так и в антисимметричном состоянии.

Так как получается два энергетических состояния, то можно сделать вывод, что должны быть и две волновые функции. Это может быть установлено с помощью общего выражения, связывающего параметры C1 и C2. В принятых теперь обозначениях это будет

36

Для получения решения, соответствующего симметричному состоянию, надо в этом уравнении вместо Е поставить Ес, а для антисимметричного состояния заменить Е на Eас. После такой замены для симметричного состояния получим:

где N — нормирующий множитель.

Чтобы получить окончательные волновые функции, необходимо нормировать функции Ψс и Ψac. Это можно показать на симметричной функции, используя условия нормирования:

Можно записать уже нормированные функции

37

По волновым функциям можно определить распределение электронного заряда в молекуле, а из выражений для энергетических состояний вычислить энергию молекулярных уровней. Рассмотрим сначала распределение заряда, можно видеть, что если S достаточно мало, то

Отсюда видно, что симметричная функция ведет к увеличению плотности электронного заряда в области перекрывания между двумя атомами по сравнению с тем, что имеет место у индивидуальных атомов, описываемых функциями ψа2 и ψb2. С другой стороны, антисимметричная функция ведет к уменьшению плотности заряда. Это изображено графически на рис. 12.

а

б

Рис. 12. Электронная плотность вдоль ядерной оси для симметричного (а) и антисимметричного (6) состояния молекулярного иона водорода.

Пунктирные линии изображают плотность заряда у индивидуальных атомов, удаленных один от другого на бесконечно большое расстояние, а сплошная линия изображает

38

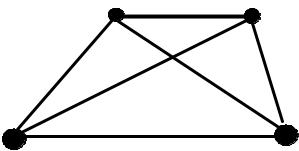
распределение электронного зарядa в молекулярном ионе водорода вдоль линии, соединяющей ядра (ядерной оси). Очевидно, что связывающая орбиталь благоприятствует такому распределению заряда, при котором он концентрируется между ядрами, в то время как разрыхляющая орбиталь ведет к уменьшению плотности заряда в этой области и к концентрации его около индивидуальных атомных ядер. Так как ковалентная связь возникает при распределении электронного заряда в области связи, то очевидно, что только симметричная функция обусловливает образование устойчивой молекулы.

3.2 Метод валентных связей. Молекулы H2

Теория валентных связей проста для понимания. Несмотря на это, метод валентных связей часто требует более сложного математического аппарата, чем теория молекулярных орбиталий, и, кроме того, установить начальную функцию для сложной молекулы не так просто, как в теории молекулярных орбиталей. Представление о теории валентных связей до известной степени можно получить при квантовомеханическом рассмотрении молекулы водорода. Эта задача была впервые удачно решена в 1927 г. Гейтлером и Лондоном.

В методе валентных связей предполагается, что если две независимые системы в отдельности описываются волновыми функциями φа и φb, то для построения из них сложной системы волновая функция будет

Эта волновая функция помещает электрон (1) у ядра а и электрон (2) у ядра b. Хотя кривая потенциальной энергии, получающаяся с помощью этой волновой функции, имеет минимум, указывая этим на устойчивость молекулы, совпадение с опытом плохое. Гораздо лучшая начальная функция получится, если учесть основной принцип квантовой механики (принцип суперпозиции). В волновой функции ΨI произвольно электрон (1) помещен у ядра а, а электрон (2) у ядра b. Для такого выбора нет основания, и вполне возможно обратное распределение

Рис. 13. Координаты электронов для молекулы водорода.

39

Это новое условие может быть введено в полную волновую функцию при использовании обычной линейной комбинации, согласно принципу суперпозиции:

Теперь, когда есть исходная функция, задача становится такой же, как и для молекулярного иона водорода. Пользуясь обозначениями рис.13, получим оператор Гамильтона для молекулы водорода

а это приводит к вековому уравнению для молекулярного иона водорода. Кроме того, получаются также выражения для энергии симметричного и антисимметричного состояния, аналогичные выражениям для молекулярного иона водорода.

Входящие в эти формулы интегралы более сложны, чем интегралы, входящие в формулы для молекулярного иона водорода. Величина H11 может быть выражена следующим образом:

Двойной интеграл возникает из-за необходимости учета координат и электрона (1), и электрона (2). После введения оператора Гамильтона интеграл принимает вид

40