ФОТП 2013

но малое количество) удельной теплоты, подводимой к термодинамической системе или отводимой от неё в случае, когда вся эта теплота q подводится к рассматриваемой системе (или отводится от неё) в условиях равновесного процесса, Дж/кг; Т текущая температура системы в условиях реализации равновесного процесса подвода теплоты q, К.

В соотношении (12.7) знак равенства относится к равновесным процессам, а знак неравенства − к неравновесным.

Например, для процессов, когда из внешней среды теплота к системе не подводится и от неё не отводится, из (12.7) следует:

О таких процессах говорят, что они протекают в адиабатных услови-

ях.

Из (12.8) следует, что если внутри термодинамической системы осуществляется какой-то неравновесный процесс, а сама система находится в адиабатных условиях, то её энтропия возрастает, так как в этом случае s > 0.

Изолированная термодинамическая система, по определению, не об-

менивается с окружающей средой никакой энергией, в том числе и энергией в форме теплоты. Таким образом, все процессы, происходящие в ней, протекают в адиабатных условиях.

Из сказанного выше вытекает важное следствие:

Энтропия изолированной системы, при наличии в ней неравновесных (необратимых) процессов, всегда возрастает.

Этот рост энтропии продолжается до тех пор, пока в системе не установитсяравновесие, то есть не прекратятся все неравновесные процессы. В состоянии равновесия энтропия изолированной системы имеет максимальное значение.

13. Третий закон термодинамики

Третий закон термодинамики называют ещё тепловой теоремой Нернста. Эту теорему сформулировал в 1906 году немецкий физик Нерст на базе широких экспериментальных исследований поведения вещества при низкой температуре.

Благодаря этой теореме энтропия s, а также другие, связанные с ней функцией состояния становятся численно определёнными и практически полезными.

41

Дело в том, что энтропия определяется через её дифференциал ds. Поэтому сама величина s определена лишь с точностью до постоянной интегрирования sо. Там, где в расчётах имеют дело с дифференциалом энтропии, эта постоянная sо не влияет на результат.

Однако, поскольку в некоторые термодинамические формулы входит произведение Т · sо. Из-за этой неопределённости практически пользоваться такими формулами было бы нельзя.

Таким образом. Встаёт вопрос об абсолютном значении энтропии. Ответом природы на этот вопрос и является теорема Нернста. В ре-

дакции Планка эта теорема звучит так:

при абсолютном нуле температуры (0, К) энтропия любого вещества принимает значение sо, не зависящее от давления, агрегатного состояния и других характеристик вещества. Эту величину sо можно принять равной нулю, получив, таким образом, абсолютную нормировку энтропии любого вещества.

То есть энтропия любой системы при абсолютном нуле всегда может быть принята равной нулю:

Это утверждение, подтверждаемое опытными данными, и называется

третьим законом термодинамики.

Примечание:

Физический смысл энтропии можно прояснить как при анализе равновесных процессов, так и при изучении неравновесных процессов. При этом более глубокий термодинамический смысл энтропии раскрывается при анализе неравновесных процессов. (Отметим, что все реальные процессы являются в той или иной мере неравновесными). Смысл этот со-

стоит в том, что изменение энтропии является мерой необратимости

процессов в замкнутой системе и характеризует направление естест-

венных процессов в такой системе.

14.Основные соотношения для расчёта процессов

видеальном газе

Во многих теплотехнических установках происходят различные процессы с веществами, находящимися в газовой фазе. Это относится к двигателям внутреннего сгорания, компрессорам, соплам, горелкам и т.п. При этом в большинстве случаев эти газы или газовые смеси можно считать

42

идеальными. То есть уравнение состояния для них имеет вид (см. раздел

2):

Для разработки технических решений по совершенствованию подобного оборудования необходимо уметь рассчитывать протекающие в нём процессы.

В этом параграфе на уровне постановки общей задачи рассматривается, каким образом рассчитываются термодинамические процессы в идеальном газе.

Любая физико-математическая модель какого-то технологического процесса строится в два этапа. Вначале описывается физическая модель, в которой определяются искомые функции. Затем составляется замкнутая система уравнений, позволяющая однозначно определить искомые функции.

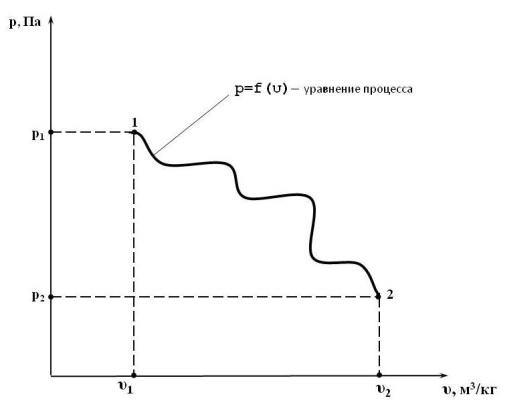
Будем считать, что в идеальном газе происходит некий произвольный равновесный (обратимый) процесс. Пусть р, Па, υ, м3/кг, и Т, К – параметры состояния газа (абсолютное давление, удельный объём и абсолютная температура соответственно). Тогда, как известно, в р υ-координатах данный процесс может быть представлен непрерывной линией р = f (υ), приведённой на рис. 14.1. Функция f (υ) называется уравнением процесса. Это непрерывная функция удельного объёма, соединяющая точки 1 и 2 – начала и конца процесса. В различных процессах f (υ) имеет свой вид. Например, в процессе при постоянном удельном объёме это вертикальная линия, а в процессе при постоянном давлении – горизонтальная линия.

Очевидно, что в общем случае в ходе процесса 1 – 2 непрерывно изменяются все параметры состояния системы (идеального газа) р, υ, Т, а также все удельные функции состояния: внутренняя энергия u, Дж/кг; энтальпия i, Дж/кг; энтропия s, Дж/(кг · К).

Основной целью построение математической модели является обретение возможности рассчитывать для конкретного случая удельные теплоту q и работу l процесса, а также значения параметров состояния в любой точке процесса.

Аналитическим основанием математической модели, описывающей процесс 1 – 2 (рис. 14.1), являются следующие четыре положения термодинамики.

Первый закон термодинамики в дифференциальной форме (см. раз-

дел….):

43

где du, dq и dl – дифференциалы (бесконечно малые приращения) удельной внутренней энергии, удельной теплоты и удельной работы процесса, Дж/кг.

Рис. 14.1. Изображение некоего равновесного процесса в р υ-координатах

Определение истинной удельной теплоёмкости для произвольного процесса (см. раздел….):

где с = с (Т, f (υ)) – истинная удельная теплоёмкость системы, зависящая в рассматриваемом общем случае не только от температуры Т, но и от вида функции уравнения процесса f (υ), Дж/(кг · К).

Общее выражение для расчёта механической работы расширения системы в ходе любого равновесного процесса, которая также зависит от вида функции f (υ) (см. раздел…….):

44

Определение удельной энтропии системы:

где ds – дифференциал удельной энтропии системы, Дж/(кг · К).

Вместе выражения (14.2) …. (14.5) образуют систему из четырёх дифференциальных уравнений:

Замечание:

Записанная в общем виде система уравнений (14.6) может быть использована для анализа процессов, происходящих в любых системах: идеальных газах; реальных газах; системах, находящихся в жидкой и твёрдой фазе.

Систему (14.6) можно рассматривать как систему дифференциальных уравнений с пятью неизвестными искомыми функциями u, q, l, s и с, аргументами которых являются параметры состояния р, υ, Т. Для наглядности можно сказать, что р, υ, и Т выполняют здесь роль подобную той, которую часто выполняют привычные в математике переменные x, y и z – декартовы координаты. Отличие заключается в том, что координаты x, y и z в математике, как правило, рассматриваются как независимые переменные, тогда как р, υ, и Т не являются независимыми переменными, а всегда связана между собой, например, для идеального газа уравнением состояния (14.1).

В силу (14.1) независимыми из трёх переменных величин р, υ, и Т могут быть только любые два, а третья однозначно определяется по их значениям из уравнения (14.1). Таким образом искомые в (14.6) функции могут рассматриваться, как функции двух независимых аргументов – любых двух из трёх параметров состояния р, υ, и Т. При этом заранее известно, что функции состояния u и s зависят только от параметров состояния и не зависят от уравнения процесса (вида функции f (υ)), тогда как остальные три искомые функции q, l и c зависят и от параметров состояния и от вида функции f (υ).

45

Так как в системе (14.6) число искомых функций больше числа уравнений, то для её однозначного разрешения требуется добавить в качестве пятого независимого уравнения какие-то дополнительные условия, которые с одной стороны, накладывают какие-то дополнительные ограничения на характер рассматриваемого процесса 1 – 2, а с другой стороны, позволяет однозначно разрешить систему (14.6).

Понятно, что это дополнительное условие должно также способствовать решению актуальных технических поблеем. Именно такими дополнительными условиями являются широко известные условия, характеризующие следующие термодинамические процессы, происходящие в газах и газовых смесях:

•при постоянном удельном объёме – изохорный (от греческих изос – одинаковый, хорос – место);

•при постоянном давлении – изобарный (аналогично, бар – сила);

•при постоянной температуре – изотермический;

•без подвода к системе и отвода от неё энергии в форме теплоты – адиабатный (от греческого адиабатос – непереходимый, т.е. система как бы окружена непроходимой для теплоты оболочкой);

•процесс, в котором параметры состояния связаны между собой соотношением

где n – постоянная величина, которая может принимать значение в интервале от –∞ до +∞.

Такой процесс называется политропным, а n – показатель политро-

пы. (Термин образован из греческих слов поли – много, тропос – тропа, путь. То есть политропный – это многотропиночный, многопутный.)

Первые четыре процесса называются основными термодинамическими процессами. Политропный процесс является обобщающим в том смысле, что все основные процессы являются частными случаями политропного процесса (подробнее см. ниже).

Для однозначного разрешения системы (14.6) помимо перечисленных выше дополнительных условий требуется задать необходимые условия однозначности, позволяющие определить значения у появляющихся в результате интегрирования констант интегрирования. Это могут быть, значения начальных и конечных температур, давлений и т.п.

В следующих разделах будет показано как решается (интегрируется) система (14.6) для перечисленных выше процессов.

46

15. Расчёт процессов в идеальном газе

15.1. Изохорный процесс

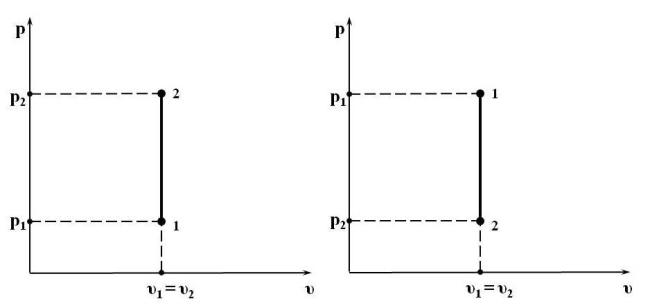
Условие, определяющее изохорный процесс: υ = const или dυ = 0. Изображение изохорного процесса в р υ-координатах представлено на

рис. 15.1 а) и б).

Рис. 15.1. Изображение изохорного процесса в р υ-координатах: а) с повышением давления; б) с понижением давления

Связь между параметрами состояния газа в начале и конце изохорного процесса получаем из уравнения состояния (13.1), записав его для точек 1

и 2:

Разделив левые и правые части (15.1) друг на друга получаем:

Для рассматриваемого случая общая система уравнений с дополнительным условием принимает следующий вид:

47

Так как при условии υ = const неизвестная в общем случае удельная теплоёмкость процесса с превращается в известную (из справочника) удельную теплоёмкость при постоянном объёме сυ, то в системе (15.3) число неизвестных функций становится равным числу независимых уравнений. То есть система (15.3) становится однозначно разрешимой. Решение дифференциальных уравнений производится, как известно, путём их интегрирования.

После интегрирования второго уравнения (15.3) с учётом, что с = сυ (для наглядности здесь и далее будем считать удельные теплоёмкости сυ и ср постоянными величинами), будем иметь:

где Т1 и Т2 – температуры газа в начале и конце процесса соответственно, К.

После интегрирования третьего уравнения (15.3) получаем:

где υ1 и υ2 – удельные объёмы газа в начале и конце процесса соответственно (υ1 = υ2), м3/кг.

После интегрирования первого уравнения (15.3) получаем, с учётом

(15.5):

После интегрирования четвёртого уравнения (15.3) получаем:

48

Выводы:

1)Из (15.2) следует, что в изохорном процессе отношение давлений равно отношению температур.

2)Из(15.5) следует, что в изохорном процессе работа не совершается (удельная работа равна нулю). (Так как при интегрировании уравнение идеального газа не использовалось, то этот вывод справедлив для всех случаев: идеального газа, реального газа, для вещества в твёрдой или жидкой фазах).

3)Из (15.6) следует, что в изохорном процессе вся теплота процесса идёт на изменение внутренней энергии газа. (Также это справедливо для всех случаев).

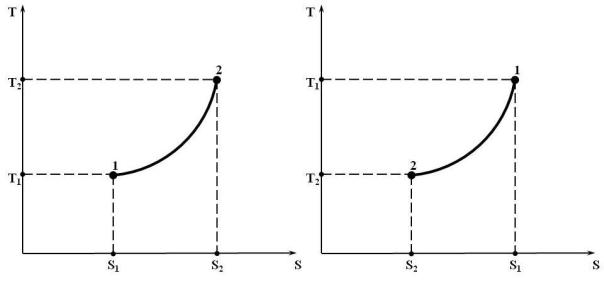
4)Из (15.7) следует, что в Ts-координатах изохорный процесс изображается логарифмической кривой рис. 15.2 а) и б) (Аналогично выводим (2)

и(3)).

Рис. 15.2. Изображение изохорного процесса в T s-координатах: а) с подводом теплоты; б) с отводом теплоты

15.2. Изобарный процесс

Условие, определяющее этот процесс: р = const или dp = 0.

49

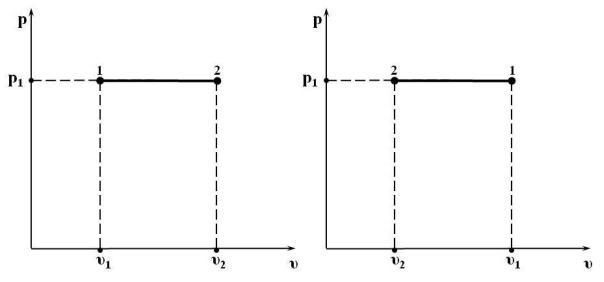
В pυ-координатах изображается горизонтальными линями на рис. 15.3.

Рис. 15.3. Изобарный процесс 1 – 2 в р υ-координатах:

а) с увеличением удельного объёма (расширение); б) с уменьшением удельного объёма (сжатие)

Соотношение между параметрами состояния в ходе изобарного процесса определяется из уравнения состояния идеального газа. Запишем его для точек 1 и 2 – начала и конца изобарного процесса:

Разделив левые и правые части (15.1) друг на друга получаем:

Равенство (15.2) показывает, что в изобарном процессе отношение удельных объёмов равно отношению температур.

Исходная система уравнений (15.6) с дополнительным условием для изобарного процесса имеет вид:

50