– постоянная величина, а
= − 3,75 3 = −11,25 кН.
– |
1 |
qz |
2 |
= 26,25 z |
|
−10z |
2 |
. (57) |
|
2 |
2 |
2 |
2 |
|
|
|
|
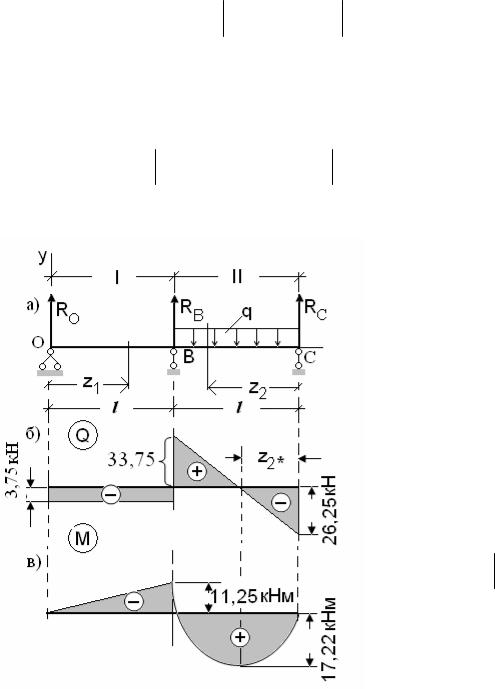
Используя аналитические выражения для Q, M (56), (57), по точкам строим эпюры Q, M (рис.18,б,в).
На первом участке перерезывающая сила изгибающий момент – линейная функция:
QI = Ro = − 3,75 кН ; MI z1 = 0 = 0; MI z1 = 3
На втором участке перерезывающая сила – линейная функция, а
изгибающий момент – квадратная парабола. Для построения эпюры QII достаточно иметь две точки:
QII z = 3 = 33,75 кН; QII z = 6 = – 26,25 кН.
Для построения эпюры MII необходимо иметь как минимум три точки. Вычисляем: при z2 = 0 МII = 0; при z2 = 3 МII = 78,75 – 90 = – 11,25 кНм.
В сечении, где перерезывающая сила QII равна нулю, изгибающий момент МII достигает экстремума (максимума). Определяем координату сечения, в котором перерезывающая сила QII равна нулю:
z2* = Rc
q = 26,25
20 =1,31м
вычисляем значение максимального изгибающего момента maxМII :
maxM = M = II II z2 =1,31
= 26,25 1,31−10 1,312=
=17,22 кНм .
Рис.18. Расчетная схема (а) и эпюры Q (б), M (в).
Эпюры Q, M представлены на рис.18,б,в.
Размеры поперечного сечения стального двутаврового профиля подбираем по условию прочности:
maxσ = maxM ≤ σ , Wx adm
где Wx – момент сопротивления сечения.
Требуемый момент сопротивления
W≥ max M ; max M = 17,22 кНм; x σadm
вычисляем:
|
17,22 103 |
|
-3 |
|
3 |
|
3 |
|
W ≥ |
|
= 0,123·10 |
|
м |
|
= 123 см |
|
. |
140 106 |
|
|
|
x |
|
|
|
|
|
|
|
По ГОСТ 8239-72* (Приложение 3) выбираем двутавр № 18. Момент сопротивления двутавра Wx = 143 см3 , площадь сечения А = 23,4 см2.
Проверяем прочность балки по касательным напряжениям на опоре
В, где Qmax = 37,5 кН.
Максимальное касательное напряжение τmax достигается в стенке
двутавра на нейтральной оси ох, поэтому τ |
= |
3 |
|
Q |
. Вычисляем: |
|
|
|
|
|
|
max |
2 |
|
A |
|
|
|
37,5 103 |
|
|
3 |
|
|
|
|
|
|
τ = |
|
|
|
= 2,4 107 Ïà |
= 24 ÌÏà . |
|
|
max |
2 |
|
23,4 10− 4 |
|
|
|
|
|
|
|
|
|
|
|
|
Так как τmax < τadm, то условие прочности по касательным напряжениям выполнено.
Поскольку при выборе двутавра № 18 было использовано условие прочности по нормальным напряжениям, прочность балки обеспечена.
3.5. Определение несущей способности статически неопределимой балки.
Пример 6. Стальная двухпролетная балка постоянного поперечного сечения нагружена в левом пролете равномерно распределенной нагрузкой интенсивностью q. Левая опора балки – шарнирно-неподвижная, две другие – шарнирно-подвижные. Поперечное сечение балки – два швеллера № 24 (условное обозначение ][ № 24). Расстояние между опорами l = 6м.
Допускаемые напряжения σadm = 140 МПа, τadm = 80 МПа. Жесткость балки EJ = const; E – модуль Юнга, J – осевой момент инерции поперечного сечения. Расчетная схема представлена на рис. 19.
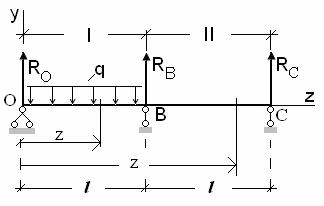
Требуется построить эпюры изгибающих моментов М и перерезывающих сил Q, а также определить несущую способность балки расчетом по допускаемым напряжениям, т.е. определить допускаемую нагрузку на балку qadm . Допускаемую нагрузку на балку qadm найдем из условия
Рис.19.Исходная расчетная схема. |
|
прочности по нормальным напряжениям |
|
maxσ= |
maxM |
≤ σ , |
(58) |
|
|
|
adm |
|
|
Wx |
|
где Wx – момент сопротивления сечения; maxM – значение максимального по модулю изгибающего момента в сечениях балки.
После определения допускаемой нагрузки на балку qadm проверим выполнение условия прочности по касательным напряжениям:
τ |
= |
3 |
|
maxQ |
≤ τ , |
(59) |
|
|
max |
|
|
|
|
adm |
|
|
|
2 A |
|
где A – площадь поперечного сечения балки; maxQ – значение максимальной по модулю перерезывающей силы в сечениях балки.
Уравнения равновесия балки:
|
|
|
|
|
6 |
|
|
|
|
ΣM(c) = 0; R |
12 + R |
6 − q 6 6 |
+ |
|
|
= 0 ; |
(60) |
|
2 |
|
o |
B |
|
|
|
|
|
|
ΣM(o) = 0; –R |
12 − R |
6 + q 6 |
6 |
= 0. |
|
(61) |
|
|
|
|
c |
B |
2 |
|
|
|
|
|
3.5.1. Определение несущей способности статически неопределимой балки с использованием метода начальных параметров.
Балка один раз статически неопределимая.
Два уравнения равновесия (60), (61) содержат три неизвестные опорные реакции RO , RB , RC; для их отыскания необходимо составить дополнительные уравнения.
Выберем начало координат на опоре O, ось z направим вправо, а ось y – вверх.
Воспользуемся тем, что прогибы на опорах B,C балки равны нулю:
vB = v |
z=6 = 0; vc = v |
z=12 = 0. |
(62) |
Прогибы на опорах B,C выразим через заданные силы по методу начальных параметров (Приложение 2). Два начальных параметра известны: vO = 0, MO = 0; два других – RO , θO следует найти. Так как появилось еще одно неизвестное – параметр θO , в дополнение к уравнениям равновесия (60), (61) составим два уравнения, отражающие условия совместности деформаций балки на опорах B,C.
Уравнение упругой линии балки на первом участке (0 ≤ z < 6м):
EJv |
|
= EJθz + R |
|
z3 |
− q |
z4 |
; |
(63) |
I |
o 6 |
|
|
o |
24 |
|
|
Уравнение упругой линии балки на втором участке (6 ≤ z < 12м):
|
|
= EJθz + R |
|
z3 |
|
|
z4 |
|
|
|
|
(z − 6)3 |
|
|
|
|
(z − 6) |
4 |
|
|
EJv |
|
|
|
|
|
|
− q |
|
|
+ R |
|
|
|
|
|
|
|
|
|
|
+ q |
|
|
|
|
. |
(64) |
II |
o |
6 |
|
24 |
|
B |
|
|
6 |
|
|
|
|
24 |
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляем (63) в первое условие (62), а |
|
|
(64) – во второе условие |
(62): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJθ |
|
6 + R 62 − q |
63 |
= 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(65) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
o |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
3 |
|
|
|
|
|
|
|
|
|
12 |
4 |
|
|
|
6 |
4 |
|
|
|
|
|
|
EJθ |
|
12 + R |
|
|
|
+ |
R |
|
62 |
− q |
|
|
− |
|
|
= 0 . |
|
|
(66) |
|
|
|
|
|
|
24 |
|
|
|
|
|
|
o |
o |
|
|
6 |
|
|
|
|
B |
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из системы уравнений (60), (61), (65), |
|
(66) выражаем |
EJθO и |
опорные реакции Ro, RB и Rc через нагрузку q: |
|
|
|
|
|
|
|
|
|
|
|
|
R |
= |
21 |
q , |
|
R |
= |
15 |
q |
, R |
|
= − |
3 |
q . |
|
|
(67) |
|
|
|
8 |
|
|
|
c |
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
B |
4 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
(Значение EJθO не выписываем, поскольку далее оно не используется).
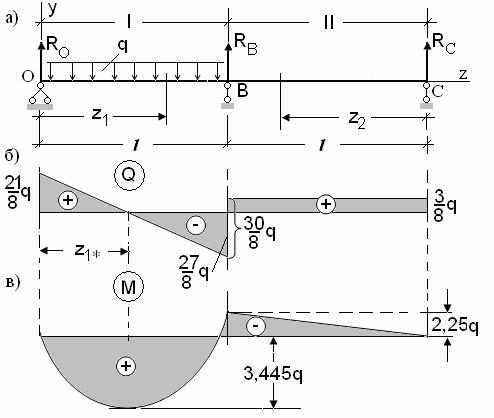
При построении эпюр Q, M используем локальные координаты z1 и
z2: z1 отсчитываем от левого конца балки (точка O), z2 – от правого конца балки (точка C), как показано на рис.20,а.
Строим аналитические выражения для Q, M по участкам. На первом участке:
|
|
|
|
21 |
|
|
I: 0 ≤ z1 |
< 6 м; Q |
= R |
− qz |
= |
|
|
− z |
q ; |
8 |
|
|
I |
o |
1 |
|
|
1 |
|
(68)
234
M = R z − |
1 |
qz2 |
= |
21 |
qz − |
1 |
qz |
2 . |
|
|
|
|
I |
o 1 |
2 |
|
|
1 |
8 |
1 |
2 1 |
На втором участке: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II: 0 ≤ z2 < 6 м; QII = – Rc = |
3 |
q ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
MII = Rcz2 |
= – |
3 |
qz |
. |
|
|
|
(69) |
|
|
|
|
|
|
8 |
|
2 |
|
|
|
|
|
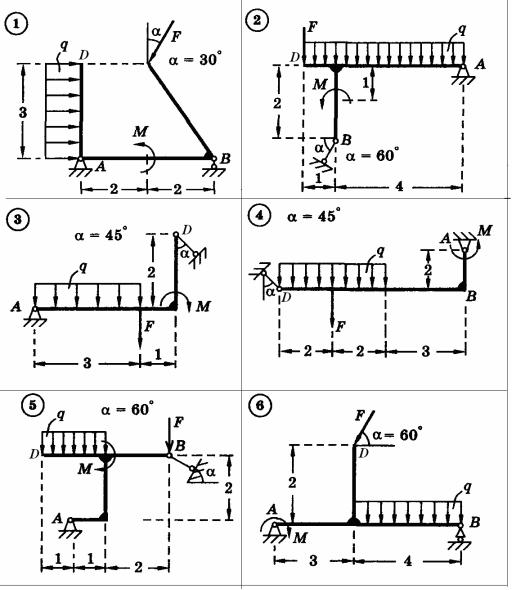
Определяем положение max М в левом пролете балки.
Рис.20. Исходная расчетная схема(а) и эпюры Q(б), M(в).
В сечении, где перерезывающая сила QI равна нулю, изгибающий момент МI достигает экстремума (максимума). Определяем координату сечения, в котором перерезывающая сила QI равна нулю:
Ro – qz1 = 0, z1* = Ro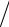
q = 21
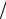8 м;
вычисляем значение максимального изгибающего момента maxМI :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
qz2 |
|
21 |
|
|
|
21 |
|
1 |
|
21 2 |
|
1 |
21 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
M |
|
= R z |
− |
|
= |
|
|
|
q |
|
|
− |
|
q |
|
|
|
= |
|
|
|
|
|
q . |
(70) |
|
|
|
I |
|
|
c 1* |
|
2 |
1* |
|
8 |
|
|
|
|
|
8 2 |
|
8 |
|
|
2 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисляем значения Q и M в характерных точках: |
|
|
|
|
= |
21 |
q − q 6 = − |
27 |
q; M |
|
|
|
|
|
|
|
= − |
3 |
q 6 = − |
9 |
q = − 2,25q ; |
(71) |
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
z = 6 |
8 |
|
|
|
8 |
|
|
|
II |
|
z = 6 |
|
8 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
21 |
2 |
maxM |
= |
|
|
|
|
|
q = 3,445q кНм. |
|
|
|
I |
|
2 |
|
8 |
|
|
|
По значениям Q и M в характерных точках (71) строим эпюры Q и M, которые представлены на рис.20,б,в.
По ГОСТ 8240-72* (Приложение 4) швеллер № 24 имеет такие геометрические характеристики: площадь поперечного сечения A = 30,6
см2 , момент сопротивления Wx = 242 см3; два швеллера A = 61,2 см2 , 2Wx
= 484 см3 .
Используя условие прочности по нормальным напряжениям (58) вычисляем допускаемую нагрузку:
max М ≤ σadm . Wx , |
3,445qadm ≤ σadm . Wx , |
|
|
140 |
106 484 |
10− 6 |
q |
≤ |
|
|
|
|
=19,67 кН м. |
|
|
3,445 |
|
adm |
|
|
|
|
|
Проверяем выполнение условия прочности по касательным напряжениям (59).
Значение максимальной по модулю перерезывающей силы в сечениях балки – max Q = 27 q = 27 19,67 = 66,38 кН .
88
τ |
= |
3 66,38 |
103 |
=16,27 МПа < τ |
|
= 80 МПа . |
|
|
|
|
|
2 61,2 10− 4 |
|
max |
|
|
adm |
|
Так как τmax < τadm, условие прочности по касательным напряжениям выполнено.
Поскольку при отыскании допускаемой нагрузки было использовано условие прочности по нормальным напряжениям, прочность балки обеспечена.
Проверяем правильность построенного решения другим методом. С этой целью используем метод сил.
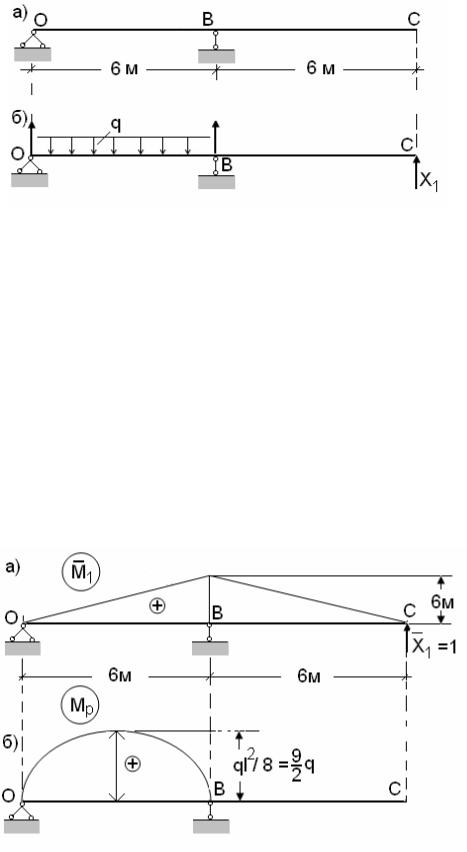
3.5.2. Определение несущей способности статически неопределимой балки с использованием метода сил. Принимаем в качестве "лишней" опорной связи шарнирно-подвижную опору С. Отбрасываем ее и заменяем опорную реакцию RC "лишней" неизвестной X1 = RC. В качестве основной системы выбираем однопролетную балку c консолью (рис.21,а).
Нагрузив основную систему силами P = {q} и опорной реакцией RC , получим эквивалентную систему (рис.21,б).
Рис.21. Основная (а) и эквивалентная (б) системы. Каноническое уравнение метода сил в данном случае имеет вид:
|
|
δ11 X1 + |
1p= 0, |
|
|
|
(72) |
в котором удельные перемещения δ11 определены формулой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
M |
M |
|
|
|
|
δ11 = |
∑ |
∫ |
1 |
1 |
dz , |
(73) |
|
|
|
|
|
|
|
|
|
|
|
к =1(l ) |
EJ |
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
1 =1 в |
где |
|
1эпюра изгибающих моментов |
от единичной силы |
|
M |
X |
основной системе.
Рис.22. Единичная эпюра (а) и эпюра Mp от заданных сил (б).
Перемещения 1p определяются в основной системе от действия сил P = {q} по формуле:
237
|
2 |
|
M M |
|
|
|
p 1 |
|
|
|
1p = ∑ |
∫ |
dz , |
(74) |
|
|
|
k =1(l |
) |
EJ |
|
|
|
k |
|
|
|
где Мp – эпюра изгибающих моментов от заданной нагрузки q в основной системе.
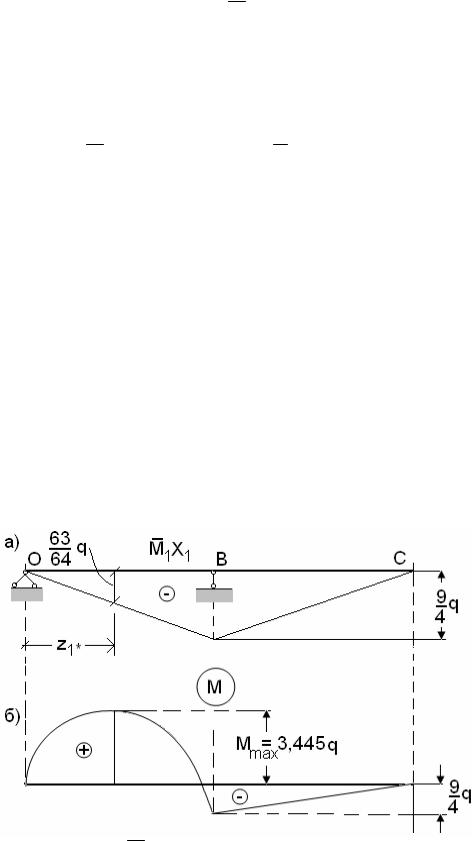
Строим эпюру M1от единичной силы X1 =1 (рис.22,а).
Строим эпюру Мp от заданной нагрузки q на левом пролете балки (рис.22,б).
Используя графоаналитический способ (Приложение 12) вычисляем
коэффициенты δ11 и |
|
1p по формулам (73) и (74): |
|
|
|
|
|
|
|
EJδ |
= 2 |
1 |
6 6 |
2 |
6 = 144 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
2 |
|
|
3 |
|
|
|
|
|
EJ |
= |
2 |
|
gl |
2 |
6 |
1 |
6 = |
gl2 |
6 = |
q 36 |
|
6 |
= 54q . |
3 |
8 |
2 |
4 |
4 |
|
|
1p |
|
|
|
|
|
|
|
|
|
|
|
|
|
По уравнению (72) вычисляем опорную реакцию Rc = X1:
R |
c |
= X = − |
1p |
= − |
6 |
9q |
= − |
3 |
q кН. |
(75) |
|
|
|
|
|
|
δ |
|
72 |
|
|
1 |
2 |
8 |
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
Рис.23. Эпюра M1X1(а) и результирующая эпюра M(б).
Из уравнений равновесия балки (60), (61) определяем опорные реакции RO , RB :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RB = – 2RC + 3q = |
3 |
q + 3q = |
15 |
q ; RO = − |
1 |
R |
|
+ |
9 |
q = − |
15 |
q + |
36 |
q = |
21 |
q . |
|
|
|
B |
|
|
|
|
4 |
|
4 |
2 |
|
2 |
8 |
8 |
|
|
8 |
|
Опорные реакции RO , RB , RC совпадают с вычисленными выше. |
|
|
Умножив эпюру |
|
1 от единичной силы |
|
|
1 =1, приложенной в |
M |
|
X |
точке C, на реакцию Rc = X1 , получим эпюру изгибающих моментов от силы Rc (рис.23,а). После наложения эпюры Мр от заданной нагрузки на эпюру M1X1 получим результирующую эпюру М – эпюру изгибающих моментов в исходной расчетной схеме (рис.23,б).
Найдем максимальный изгибающий момент Mmax. Координата сечения, в котором изгибающий момент достигает максимального
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значения, равна z1* = Ro |
q = 21 8 м. Подставляем |
z1* в выражение M = |
Mp + |
|
1X1; получаем максимальный изгибающий момент |
M |
|
|
Mmax = M |
|
z= |
21 = |
1 |
q 6 |
21 |
– |
1 |
q ( |
21 |
)2 – |
9 |
q |
21 |
= |
|
|
|
|
|
|
|
|
|
|
|
4 6 |
|
|
|
|
|
8 |
2 |
8 2 |
8 |
|
|
8 |
|
= 7,875q – 4,43q = 3,445q кНм.
Максимальный изгибающий момент Mmax и опорные реакции Ro, RB, Rc совпадают с найденными расчетом при использовании универсального уравнения прогибов балки, следовательно, выполненный расчет правильный.
Эпюра изгибающих моментов на рис.23,б совпадает с эпюрой на рис.20,в.
Таким образом, допускаемая нагрузка на балку qadm определена правильно.
Расчеты закончены.
Задание № 12. Расчет плоских статически определимых рам
Для рам, расчетные схемы которых представлены на рис.1,а,б,в,г, требуется построить эпюры продольных (N) и перерезывающих (Q) сил, а также изгибающих моментов (M); определить перемещения точки D и угол поворота сечения стержней в точке A.
Нагрузки на рамы: F = 10 кН, M = 10 кН·м, q = 5 кН/м. Размеры указаны в метрах. Осевые моменты инерции J сечений стержней рам равны 5·10-4 м4: J = 5·10-4 м4; модуль упругости E = 30 ГПа.
Номер расчетной схемы выбирается по коду из трех цифр n2n1n0, выданному преподавателем; n2, n1, n0 – три цифры кода студента: n2 – первая слева цифра, n1 – вторая слева цифра, n0 – последняя цифра кода.
Рис.1,а. Расчетные схемы рам 1÷6.
