Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Финансовый университет при Правительстве РФ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lin_Alg-BE

.pdf

Скачиваний:

Добавлен:

13.03.2015

Размер:

1.01 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

Конспект по линейной алгебре

Виталий Геннадьевич Курбатов

6 декабря 2011 г.

Оглавление

1 Матрицы и определители		3
1.1	Матрицы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	3
1.2	Операции над матрицами . . . . . . . . . . . . . . . . . . . . . . . . . . .	4
1.3	Определители второго порядка . . . . . . . . . . . . . . . . . . . . . . .	6
1.4	Определители третьего порядка . . . . . . . . . . . . . . . . . . . . . . .	7
1.5	Свойства определителей . . . . . . . . . . . . . . . . . . . . . . . . . . .	8

1.6Символ суммирования . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

1.7Миноры и алгебраические дополнения . . . . . . . . . . . . . . . . . . . 9

1.8Определители n-го порядка . . . . . . . . . . . . . . . . . . . . . . . . . . 10

1.9Метод элементарных преобразований вычисления определителя . . . . 10

1.10Ранг матрицы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

1.11Метод элементарных преобразований вычисления ранга . . . . . . . . . 12

1.12Обратная матрица и ее нахождение методом присоединенной матрицы 13

2 Системы линейных уравнений		15
2.1	Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	15
2.2	Метод Крамера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	16
2.3	Матричная запись системы линейных уравнений . . . . . . . . . . . . .	18
2.4	Метод обратной матрицы . . . . . . . . . . . . . . . . . . . . . . . . . . .	19
2.5	Матричные уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20
2.6	Метод Гаусса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	20
2.7	Несовместная система . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	24
2.8	Неопределенная система . . . . . . . . . . . . . . . . . . . . . . . . . . .	25
2.9	Система линейных однородных уравнений . . . . . . . . . . . . . . . . .	27
2.10	Понятие о модели Леонтьева . . . . . . . . . . . . . . . . . . . . . . . . .	28

3 Векторы в трехмерном пространстве		29
3.1	Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	29
3.2	Числовая проекция вектора . . . . . . . . . . . . . . . . . . . . . . . . .	30
3.3	Декартова система координат . . . . . . . . . . . . . . . . . . . . . . . .	32

3.4Скалярное произведение . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

3.5Выражение скалярного произведения через координаты . . . . . . . . . 34

3.6Угол между двумя векторами . . . . . . . . . . . . . . . . . . . . . . . . 36

4 Арифметическое векторное пространство		37
4.1	Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	37
4.2	Линейная независимость . . . . . . . . . . . . . . . . . . . . . . . . . . .	38

December 6, 2011 Курбатов В.Г.

4.3Размерность и базис . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

4.4Скалярное произведение в n-мерном пространстве . . . . . . . . . . . . 40

	4.5	Ортогональные векторы . . . . . . . . . . . . . . . . . . . . . . . . . . .	41
5	Линейные операторы		42
	5.1	Понятие линейного оператора . . . . . . . . . . . . . . . . . . . . . . . .	42
	5.2	Матрица линейного оператора . . . . . . . . . . . . . . . . . . . . . . . .	42
	5.3	Собственные значения и собственные векторы . . . . . . . . . . . . . . .	44
6	Квадратичные формы		46
	6.1	Определение квадратичной формы, ее матрица . . . . . . . . . . . . . .	46
	6.2	Канонический вид и закон инерции . . . . . . . . . . . . . . . . . . . . .	47
	6.3	Знакоопределенные квадратичные формы . . . . . . . . . . . . . . . . .	48
7	Элементы аналитической геометрии		50
	7.1	Уравнение линии на плоскости . . . . . . . . . . . . . . . . . . . . . . . .	50
	7.2	Уравнение прямой с угловым коэффициентом . . . . . . . . . . . . . . .	50
	7.3	Общее уравнение прямой . . . . . . . . . . . . . . . . . . . . . . . . . . .	52
	7.4	Уравнение прямой, проходящей через две заданные точки . . . . . . . .	52
	7.5	Условие параллельности и перпендикулярности прямых . . . . . . . . .	53
	7.6	Кривые 2-го порядка, их общее уравнение . . . . . . . . . . . . . . . . .	54
	7.7	Выделение полного квадрата . . . . . . . . . . . . . . . . . . . . . . . . .	55
	7.8	Эллипс . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	56
	7.9	Гипербола . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	57
	7.10	Парабола . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	59
	7.11	Уравнение плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	59
	7.12	Уравнение прямой . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	62

Глава 1 Матрицы и определители

1.1 Матрицы

Матрицей называют прямоугольную таблицу, состоящую из чисел. Для краткого обозначения матриц обычно используют латинские буквы A; B; C; : : : . Например,

A =	0	1	2	3	¡2	1	:
		1	2	14	7
	@¡2		8	¡9	0; 5A

В матрицах выделяют строки и столбцы.
Когда говорят о произвольной матрице, ее обычно записывают в виде
0	1

a11 a12

BBa21 a22

A = B

@ . .

am1 am2

: : : a1n

: : : a2n CC:

... . C

: : : amn

Числа aij называют элементами матрицы. Заметим, что элементы матрицы ai1; ai2; : : : ; ain, имеющие одинаковый первый индекс i, образуют i-ю строку матрицы. Аналогично,

элементы a1j; a2j; : : : ; amj образуют j-ый столбец. Таким образом, первый индекс i в обозначении aij совпадает с номером строки, а второй j с номером столбца.

Если хотят подчеркнуть, что матрица A состоит из элементов aij, то пишут A =

faijg.

Выражение1) m £ n называют размером матрицы. Например, у матрицы

A =	0	1	2	3	¡2	1	:
		1	2	14	7
	@¡2		8	¡9	0; 5A

размер 3 £ 4.

Две матрицы A = faijg è B = fbijg считают равными, если совпадают их размеры и равны соответствующие элементы, т. е. aij = bij äëÿ âñåõ i è j.

1)Говоря выражение вместо число , имеют в виду, что умножение в конструкции m£n остается невыполненным.

December 6, 2011 Курбатов В.Г.

Åñëè m = n, то матрицу называют квадратной, а если m =6 n, то просто

прямоугольной.

Пусть A квадратная матрица. Eе главной диагональю или просто диагональю называют множество элементов a11, a22, . . . , ann, имеющих одинаковые индексы, т.

е. главная диагональ идет из левого верхнего угла в правый нижний, а побочная
диагональ из левого нижнего угла в правый верхний.
Квадратную матрицу называют диагональной, если все ее элементы, стоящие вне
главной диагонали, равны нулю:
0	d	0		: : :	0	1
0	01	d2		: : :	0	1
B . .				...	.	C	:
B	0	0		: : : dnC
B						C
@						A
Например,	00		¡2 01			:
	00		¡2 01			:
		5		0	0
	@0			0	8A

Åñëè âñå di равны 1, то матрицу называют единичной и обозначают буквой E, à åñëè âñå di равны 0, то нулевой и обозначают буквой O:

00	1	: : :	01	00	0	: : :	01
1	0	: : :	0	0	0	: : :	0

	E = B. . ...		.C	;	O = B.		.	...	.C	:
	B0 0 : : : 1C					B0 0 : : : 0C
	B		C			B			C
Например,	@		A			@			A
Например,	E = 0 1		;		E =	00	1	01:
	E = 0 1		;		E =	00	1	01:
	1	0	¶			1	0	0
	1	0				@0		1A
	µ					@0	0	1A

Матрицу называют треугольной (или, подробнее, верхне-треугольной), если все
ее элементы, стоящие ниже главной диагонали, равны нулю:
0	0	a22	: : : a2n			1
	a11	a12	: : : a1n			C
B .		.	...	.		C	:
B						C
@						A
B	0	0	: : : annC
Например,	5	4	¡4
	5	4	¡4	A
	@0	0	8	A
	00	¡2	9	1	:

1.2 Операции над матрицами

Транспонированной по отношению к матрице A называют матрицу, столбцами которой являются строки матрицы A. Обозначение: A0.

December 6, 2011 Курбатов В.Г.								5
Пример 1. Если						0		41:
A =	0	¡4	1	;	òî A0 =	0	2	41:
µ				¶		¡3		1
	1	2	3				1	0
			¡			@		¡ A

Суммой (разностью) двух матриц A = faijg è B = fbijg называют матрицу

C = fcijg, состоящую из элементов cij = aij + bij (cij							= aij ¡ bij). Обозначение:
C = A + B (èëè C = A ¡ B). Можно складывать только матрицы одинакового
размера.
1	2	3		3	2	4
Пример 2. Пусть A = µ0	¡4	1¶ è B =		µ1	¡2	1¶. Тогда
	1 + 3		2 + 2	3 + 4		4	0	7
A + B = µ0 + 1			¡4 ¡ 2	1 + 1¶		= µ1	2	2¶:

Произведением числа ¸ и матрицы A = faijg называют матрицу C = fcijg, ñî-

стоящую из элементов cij = ¸aij. Обозначение: C = ¸A.				µ0	¡12	3¶.
Пример 3. Пусть ¸ = 3 è A =	µ0	¡4	1¶. Тогда 3A =	µ0	¡12	3¶.
	1	2	3	3	6	9

Произведением матрицы A = faijg размера m £ n на матрицу B = fbijg размера n £ k называют матрицу C = fcijg размера m £ k, элементами которой являются всевозможные произведения строк матрицы A на столбцы матрицы B. Обозначение:

C = A ¢ B èëè C = AB. Это определение не является полным.
Пример 4. Пусть A = 0					¡4	1 è B = 0		1	01. Тогда
				µ		¶		¡2	3
				1	2	3		1	1
			µ0				@		A
	¢		µ0	¢¢ 1 + 4 ¢ (¡1) + 1 ¢ 2			0 ¢ 1 + 4 ¢ 0 + 1 ¢ 3¶ µ¡2 3¶
A		B =	1	1 ¡ 2 ¢ (¡1) + 3 ¢ 2			1 ¢ 1 ¡ 2 ¢ 0 + 3 ¢ 3			=	9 10 :

Таким образом, элемент cij, стоящий на пересечении i-ой строки и j-го столбца, равен произведению i-й строки матрицы A è j-го столбца матрицы B2). Поэтому

умножить A íà B можно только в том случае, когда длина строк матрицы A совпадает с высотой столбцов матрицы B, т. е. внутренние размеры n в выражениях m £ n è n £ k должны оказаться равными. А размером произведения AB будет выражение m £ k, равное произведению внешних размеров в выражениях m £ n è

n £ k.

Пример 5. Пусть B = 0

è A =

¡4

. Тогда

¡2

1 (¡2) + 1 ¢ 4

1 ¢ 3 + 1 ¢ 1

1 + 1 0

A =

¢1 1 +¢0

1 ¢

(¡2) + 0 ¢ 4 ¡1 ¢ 3 + 0 ¢ 11

@2¡¢ 1¢+ 3 ¢ 0

¡2 ¢¢

(¡2) + 3 ¢ 4

2 ¢ 3 + 3 ¢ 1A

@¡2

¡9A

2)Совсем аккуратно: элемент cij вычисляется по формуле cij = ai1b1j + ai2b2j + ¢ ¢ ¢ + ainbnj.

December 6, 2011 Курбатов В.Г.

Уже эти примеры показывают, что A ¢ B 6= B ¢ A.

Отметим равенства: A + O = O + A = A, A ¡ A = O, A ¢ O = O ¢ A = O,

A ¢ E = E ¢ A = A:

Здесь E единичная, а O нулевая матрицы соответствующих размеров.

Отметим тождество:	(AB)0 = B0A0:

Пример 6. Пусть для изготовления одного стула требуется 4 единицы древесины и
1 единица материи, а для изготовления одного кресла требуется 6 единиц древесины
и 5 единиц материи. Предположим, что мы хотим изготовить x стульев и y кресел.
Тогда расход материалов описывается следующим произведением матриц
µ материя	¶ = µ1	5¶µy¶:
древесина	4	6 x

1.3 Определители второго порядка								a11a22¡a12a21,
обозначаемое символами	A = ¡a21	a22 ¢		2£2				a11a22¡a12a21,
Определителем матрицы	a11	a12	размера		¯1.	называют число
Это правило удобно представлять себе в виде рис.					¯1.		¯
;	det A;		jAj;		a11	a12	¯:
;	det A;		jAj;		¯a21	a22	¯:

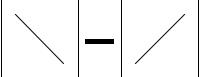
Рис. 1: Диаграмма для вычисления определителя 2-го порядка.

December 6, 2011 Курбатов В.Г.							7
Пример 7. Если A =	µ3	4¶, òî
	2	1
		=		2	1		= 2 ¢ 4 ¡ 1 ¢ 3 = 5:
		=	¯3 4¯				= 2 ¢ 4 ¡ 1 ¢ 3 = 5:
			¯			¯
			¯			¯
			¯			¯

Замечание 1. Определители первого порядка обычно не рассматривают. Удобно считать, что определитель матрицы, состоящей из одного числа (т. е. матрицы размера 1 £ 1), равен этому числу.

1.4 Определители третьего порядка

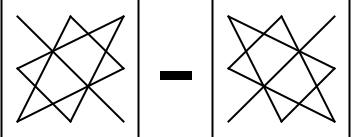
Определителем матрицы A размера 3 £ 3 называют число, вычисляемое по правилу, изображенному на рис 2. Обозначение прежнее.

Рис. 2: Правило треугольника вычисления определителя 3-го порядка.

Можно указать и аналитическую формулу:						¯ =
= det A = A =	¯a21		a22	a23
	¯	a11	a12	a13		¯
j j			a	a
	¯a					¯
	¯					¯
	¯	31	32		33	¯
	¯					¯

=¡a11a22a33 + a12a23a31 + a13a21a32 ¢

¡a13a22a31 + a12a21a33 + a11a23a32 :

Пример 8.

6¯

¡0

¯¡4

2¯

= 1

2 + (

(

2)¯

4 + 3

¯(

¡¡

¯ ¢

¢¯

¡ ¡

¢= 0¢

48 +¢

15¢

0 + 30 4 = 7: ¢

4 + 1 6 (

5) + (¡2) ¢ (¡1) ¢ 2 =

Задача 1. Вычислите определители матриц

B =

02 3 ¡21

A =

04 ¡2 0

;

¡3

5 ¡1

@2 1 ¡1A

@4 2 6 A

Ответ: jAj = 0, jBj = ¡4.

December 6, 2011 Курбатов В.Г.

1.5Свойства определителей

Âэтом параграфе обсуждаются свойства определителей третьего порядка. Полезно уже сейчас иметь в виду, что точно такие же свойства имеют место и для определителей любого порядка.

Свойство 1. При транспонировании матрицы ее определитель не меняется: jA0j =

jAj.

Свойство 2. Если поменять местами две строки (или два столбца), то определитель изменит знак на противоположный, но по абсолютной величине не изменится.

Свойство 3. Определитель, имеющей две одинаковые строки (или два одинаковых столбца), равен нулю.

Свойство 4. Если строку (столбец) определителя умножить на некоторое число, то определитель умножится на это число. Общий множитель из строки (столбца) можно выносить за знак определителя.

Свойство 5. Определитель, имеющий две пропорциональные строки (или столбца) равен нулю.

Свойство 6. Если определитель имеет нулевую строку (или столбец), то он равен нулю.

Свойство 7. Если определители

1 è

2 отличаются только k-ми строками (столб-

цами), то их сумма

1 + 2 равна определителю

, k-ая строка (столбец) которого

является суммой k-х строк (столбцов) определителей

2, а остальные строки

(столбцы) такие же как в определителях

1 è

2. Например, если k = 2, òî

¯a21 a22 + a220

a23

¯ =

¯a21 a22 a23

¯a21

a220

a23

¯:

¯a

+ a0

¯a

a11

a12

+ a120

a13

a11

a12

a13

a11

a120

a13

-ëèáî åãî

Свойство 8. Определитель¯

не изменится,¯ ¯

åñëè ê¯

какой¯

¯строке (столбцу)

прибавить другую строку (столбец), умноженную на число.

Обоснование:

¯ =

¯a21

¯:

¯a21

a22 + a21

a23

a22 a23

a21

a23

¯a

+ a

¯a

a11

a12

+ a11

a13

a11

a12

a13

a11

a13

элементов,

Свойство 9. Определитель¯

треугольной¯ ¯

матрицы¯

равен¯ произведению¯

стоящих на главной диагонали.

Например,

¯0 5 ¡4¯

= 3

¯0

¡2

Свойство 10. Определитель произведения двух матриц A è B равен произведению определителей этих матриц: jABj = jAj ¢ jBj.

December 6, 2011 Курбатов В.Г.

1.6 Символ суммирования

Для сокращенного обозначения суммы нескольких однотипных слагаемых ис-

пользуют символ

. Правила его использования аналогичны использованию опе-

ратора цикла DO

в программировании.

Выражение k=1

k2 читают так: сумма по k от 1 до 3 выражений k2 . Это выраже-

ние является

сокращенной записью суммы

+ 2

+ 3

Пример 9.

;

m=2

i2 = 32 + 42 + ¢ ¢ ¢ + n2;

cij =

aikbkj:

1.7 Миноры и алгебраические дополнения

Вычеркнем из определителя i-ю строку и j-й столбец. В результате получим опре-

делитель меньшего порядка, который называют минором элемента aij и обозначают Mij. А величину

Aij = (¡1)i+jMij

называют алгебраическим дополнением элемента aij.

Пример 10. Если =

¯2

¡3

¡6¯, òî

¯4

2¯

¯3

= 0 + 12 = 12;

M23

= ¯4

¡0¯

2+3¯

¯¡

M23

12 =

12;

A23 =(¯

3+1

M31 = ¯¡3

¡6¯ = ¡18 + 3 = ¡15;

15:

A31

=(¯

¯M31

= 1

(

15) =

¯¡

¢¯

¢ ¡

Свойство 11 (теорема Лапласа). Сумма произведений элементов aij произвольной

строки (или столбца) определителя на алгебраические дополнения Aij этих элемен- тов равна определителю:

	X3
	3
=	j=1 aijAij;	i = 1; 2; 3;
= Xi=1 aijAij;		j = 1; 2; 3:

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.03.2015318.02 Кб35linalgebra.pdf
#
13.03.201596.2 Кб175LindaHoku.МПУР.С оглавлением.docx
#
13.03.2015561.15 Кб39lineynaya_algebra.pdf
#
25.09.20194.41 Mб13Lingvisticheskoe_obespechenie.docx
#
13.03.2015328.1 Кб33Linux part 2.pdf
#
13.03.20151.01 Mб16Lin_Alg-BE.pdf
#
13.03.201557.34 Кб17Logicheskie_zadania.doc
#
13.03.201547.31 Кб133Logika_-_kontrolnaya_TsVET (1).docx
#
21.11.20192.16 Mб4LR10-ITN-22-fevralya-2011-Got.doc
#
21.07.20191.2 Mб4Lvs Mitrohov S.docx
#
13.03.2015635.79 Кб24Lyubimtseva_S_N__Koreneva_V_N_L_93_Kurs_angli.PDF