
Lin_Alg-BE
.pdfГлава 7 Элементы аналитической геометрии
7.1 Уравнение линии на плоскости
С интуитивной точки зрения линия это след, оставляемый движущейся точкой. Уравнением линии называют уравнение, которому удовлетворяют координаты каждой точки, принадлежащей данной линии, но не удовлетворяют координаты лю-
бой точки, не принадлежащей данной линии. Например, y = x2, x2 + y2 = 1.
Правило: Чтобы проверить, принадлежит ли точка линии, надо координаты точки подставить в уравнение линии.
Различают два типа уравнений:
y = f(x); F (x; y) = 0:
(7.1)
(7.2)
Примеры таких уравнений:
y = ex; x2 + y2 = 1:
В уравнении (7.1) неизвестная y явно выражена через x. Такой способ задания называют явным. Чтобы, зная x, с помощью уравнения (7.2) найти y, надо это уравнение
решить. Такой способ задания называют неявным.
Правило: чтобы найти точку (точки) пересечения двух линий, надо выписать систему, состоящую из уравнений этих линий, и решить ее.1)
7.2 Уравнение прямой с угловым коэффициентом
Уравнением прямой с угловым коэффициентом называют уравнение вида
y= kx + b:
Âнем коэффициент k имеет геометрический смысл тангенса угла между осью X и прямой.2) Число k называют угловым коэффициентом прямой. Если k > 0, òî

December 6, 2011 Курбатов В.Г. |
51 |
b |
|
b |
|
Рис. 1: Слева: k > 0; справа k < 0 |
|
график прямой возрастает. А если k < 0, то график прямой убывает. Число b имеет |
|
геометрический смысл координаты точки пересечения прямой с осью Y . |
|
Правило: Угловой коэффициент это то, на что умножается x в явном уравне- |
|
нии прямой. Примеры: 2y + 4x = 6 è y = ¡2x + 3. |
|
1)Часто это правило формулирует не вполне корректно: надо приравнять y. Это путь можно
реализовать только при условии, что оба уравнения являются явными. 2)Отсчитываемого в направлении от оси к прямой.

December 6, 2011 Курбатов В.Г. |
52 |
Задача 29. Составьте уравнение прямой, проходящей через заданную точку (x0; y0) с заданным угловым коэффициентом k.
Решение. Ответом является уравнение
y ¡ y0 = k(x ¡ x0):
Эту формулу надо знать наизусть.
7.3 Общее уравнение прямой
Не все прямые можно задать уравнением с угловым коэффициентом. А именно, исключением является вертикальная прямая (см. рис. 2):
x = a:
Общим уравнением прямой называют уравнение
Ax + By + C = 0
в предположении, что хотя бы одно из чисел A; B не равно нулю. Это уравнение охватывает все типы прямых.
Рис. 2: Вертикальная прямая
7.4 Уравнение прямой, проходящей через две заданные точки
Задача 30. Составьте уравнение прямой, проходящей через две заданные точки (x0; y0)
è (x1; y1).

December 6, 2011 Курбатов В.Г. |
53 |
||||
Решение. Ответом является уравнение |
|
|
|
||
|
|
|
|
|
|
|
y ¡ y0 |
= |
x ¡ x0 |
: |
|
|
y1 ¡ y0 |
x1 ¡ x0 |
|
||
Универсальный способ построения прямых: надо нарисовать две точки, лежащие на прямой, и провести через них прямую.
7.5Условие параллельности и перпендикулярности прямых
Теорема 38. Пусть даны две прямые y = k1x + b1 è y = k2x + b2. Для того чтобы эти прямые были параллельны, необходимо и достаточно, чтобы
k1 = k2:
Для того, чтобы прямые были перпендикулярны, необходимо и достаточно, чтобы
k1k2 = ¡1:
Рис. 3: Идея доказательства теоремы 38
Задача 31. Дана прямая 2y +3x¡7 = 0. Составьте уравнения двух прямых, проходя-
щих через точку (5; 9), одна из которых параллельна, а другая перпендикулярна исходной.
Решение. Выясним, какой угловой коэффициент у исходной прямой: (Угловой коэффициент это то, на что умножается x в явном уравнении прямой.)
y = ¡ |
3 |
x + |
7 |
; |
k1 = ¡ |
3 |
: |
|
|
|
|
|
|||||
2 |
2 |
2 |
||||||
Выпишем уравнение параллельной прямой (используя задачу 29: y ¡ y0 = k(x ¡
x0)):
y ¡ 9 = ¡32(x ¡ 5):

December 6, 2011 |
Курбатов В.Г. |
54 |
Выпишем уравнение перпендикулярной прямой (используя условие перпендикуляр- |
||
ности k1k2 = ¡1): |
|
|
|
2 |
(x ¡ 5): |
|
y ¡ 9 = 3 |
|
7.6 Кривые 2-го порядка, их общее уравнение |
||
Уравнением 2-го порядка называют уравнение вида |
||
|
a11x2 + 2a12xy + a22y2 + 2b1x + 2b2y + c = 0: |
|
Линию, задаваемую уравнением 2-го порядка, называют кривой 2-го порядка. |
||
При замене координат уравнение может упрощаться. Путем поворота системы |
||
координат можно добиться того, чтобы a12 |
= 0, а путем сдвига, как правило, допол- |
|
нительно чтобы b1 = b2 = 0. Получающееся уравнение называют каноническим. |
||
Нормальным уравнением окружности называют уравнение |
||
|
x2 + y2 = R2: |
|
Оно задает окружность радиуса R с центром в начале координат. |
||
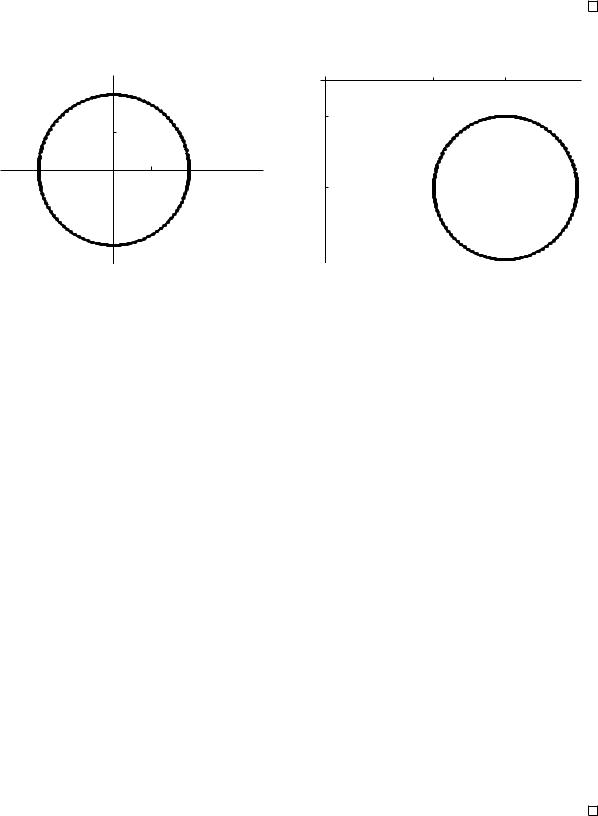
Сдвигая начало координат в точку (x0; y0), получаем уравнение |
||
|
(x ¡ x0)2 + (y ¡ y0)2 = R2: |
|
Правило. Кривая F (x ¡ x0; y ¡ y0) = 0 получается из кривой F (x; y) сдвигом |
||
вправо на x0 и сдвигом вверх на y0. |
|
|
|
Y |
Y |
|
R |
|
|
|
|
-R |
X |
y0 |
R |
|
|
|
|
X |
|
|
x0 |
|
-R |
|
|
Рис. 4: Окружности |
|
December 6, 2011 |
Курбатов В.Г. |
|
55 |
|
Задача 32. Изобразить кривую (x ¡ 5)2 + (y + 3)2 = 4. |
|
|
||
Решение. Это окружность, получающаяся из окружности x2 + y2 |
= 4 путем |
|||
сдвига на вектор (5; ¡3). Окружность x2 + y2 = 4 имеет радиус 2. |
|
|
||
Y |
|
Y |
|
|
|
|
3 |
5 |
X |
|
|
|
||
|
|
-1 |
|
|
1 |
|
|
|
|
|
1 |
X |
|
|
|
2 |
|
|
|
|
|
-3 |
|
|
Рис. 5: Окружности
7.7 Выделение полного квадрата
Полным квадратом называют выражение
a2 + 2ab + b2;
поскольку его можно преобразовать к виду (a + b)2. Выделение полного квадрата
важная процедура при построении кривых второго порядка. Например, уравнение
ax2 + ay2 + 2b1x + 2b2y + c = 0;
называемое общим уравнением окружности, всегда можно привести к виду
(x ¡ x0)2 + (y ¡ y0)2 = R2:
Задача 33. Выделить полный квадрат в выражении x2 ¡ 6x + 5.
Решение. Имеем
x2 ¡ 6x + 5 = x2 ¡ 2x ¢ 3 + 32 ¡ 32 + 5
= (x2 ¡ 2x ¢ 3 + 32) ¡ 4 = (x ¡ 3)2 ¡ 4:
Такое преобразование удобно, например, для построения графика функции y = x2 ¡
6x + 5.
Задача 34. Построить кривую x2 ¡ 10x + y2 + 6y + 30 = 0.

December 6, 2011 Курбатов В.Г. |
|
|
|
|
|
56 |
|
Решение. Выделяем полные квадраты: |
|
|
|
|
|
||
|
x2 ¡ 10x + y2 + 6y + 30 = 0 |
|
|
||||
|
x2 ¡ 2x ¢ 5 + y2 + 2y ¢ 3 + 30 = 0 |
|
|
||||
|
x2 ¡ 2x ¢ 5 + 52 ¡ 52 + y2 + 2y ¢ 3 + 32 ¡ 32 + 30 = 0 |
|
|||||
|
(x2 ¡ 2x ¢ 5 + 52) + (y2 + 2y ¢ 3 + 32) + 30 ¡ 52 ¡ 32 = 0 |
|
|||||
|
(x ¡ 5)2 + (y + 3)2 ¡ 4 = 0: |
|
|
||||
Получилось уравнение из задачи 32. |
|
|
|
|
|
||
7.8 |
Эллипс |
|
|
|
|
|
|
Эллипсом называют кривую, заданную уравнением |
|
|
|||||
|
|
x2 |
y2 |
|
|
|
|
|
|
a2 + b2 |
= 1: |
|
|
|
|
А само уравнение называют каноническим уравнением эллипса. Числа a è b называ- |
|||||||
полуосями, а точки пересечения с осями вершинами. |
|
|
|||||
þò Точки с координатами (c; 0) è (¡c; 0), ãäå c = pa2 |
¡ b2, |
называют фокусами. |
|||||
|
Y |
|
|
|
|
Y |
|
|
|
|
|
|
b |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-a -c |
c |
X |
|
-a |
-c |
c |
X |
a |
|
a |
|||||
|
-b |
|
|
|
|
-b |
|
|
|
|
|
|
|
|
|
|
|
Рис. 6: Эллипсы |
|
|
|
||
Задача 35. Определить вид и расположение кривой x2 ¡ 6x + 4y2 ¡ 16y + 21 = 0, приведя ее уравнение к каноническому виду.

December 6, 2011 Курбатов В.Г. |
57 |
Решение. Выделяем полные квадраты:
x2 ¡ 6x + 4y2 ¡ 16y + 21 = 0
x2 ¡ 2x ¢ 3 + 4(y2 ¡ 2 ¢ y ¢ 2) + 21 = 0
x2 ¡ 2x ¢ 3 + 32 ¡ 32 + 4(y2 ¡ 2 ¢ y ¢ 2 + 22 ¡ 22) + 21 = 0 (x2 ¡ 2x ¢ 3 + 32) + 4(y2 ¡ 2 ¢ y ¢ 2 + 22) + 21 ¡ 32 ¡ 4 ¢ 22 = 0 (x ¡ 3)2 + 4(y ¡ 2)2 ¡ 4 = 0
(x ¡ 3)2 + (y ¡ 2)2 = 1: 22 12
Получился эллипс с центром в точке (3; 2) и полуосями 2 и 1. В качестве вспомогательного построения сначала рисуем прямоугольник с нужными полуосями. 
Y
3
2
1
|
|
|
|
|
|
X |
|
|
|
|
|
|
|||
1 |
3 |
5 |
|||||
|
|
Рис. 7: Эллипс из задачи 35 |
|
|
|
|
|
7.9 Гипербола
Гиперболой называют кривую, заданную уравнением
x2 ¡ y2 = 1: a2 b2

December 6, 2011 Курбатов В.Г. |
58 |
Само уравнение называют каноническим уравнением гиперболы. Числа a è b íà-
зывают полуосями, а точки пересечения с осями вершинами. Прямые y = §ab x называют асимптотами гиперболы. Если a = b гиперболу называют равносторонней. Точки с координатами (c; 0) è (¡c; 0), ãäå c = pa2 + b2, называют фокусами.
|
Y |
|
Y |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
b |
|
b |
|
|
-c-a |
X |
-a |
|
X |
|
a c |
|
a |
|||
|
-b |
|
-b |
|
|
|
|
|
-c |
|
|
|
Рис. 8: Гиперболы с уравнениями xa22 |
¡ yb22 |
= 1 è ¡xa22 |
+ yb22 |
= 1 |
Правило рисования: Сначала рисуют прямоугольник с полуосями a è b, затем
через его верши1íы проводят асимптоты, а затем саму гиперболу.
Кривая y = x является равносторонней гиперболой, повернутой по отношению к канонической на угол 450.
|
|
|
Y |
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
-3 |
-2 |
-1 |
1 |
2 |
X |
3 |
|||||
|
|
|
-1 |
|
|
|
|
|
-2 |
|
|
|
|
|
-3 |
|
|
|
|
|
Рис. 9: Гиперболы |
||
|
|
|
Y |
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
-3 |
-2 |
-1 |
1 |
2 |
X |
3 |
|||||
|
|
|
-2 |
|
|
|
|
|
-4 |
|
|
y = x1 |
è y = ¡x1 |
|
|
|
|
December 6, 2011 Курбатов В.Г. |
|
|
59 |
|
7.10 |
Парабола |
|
|
|
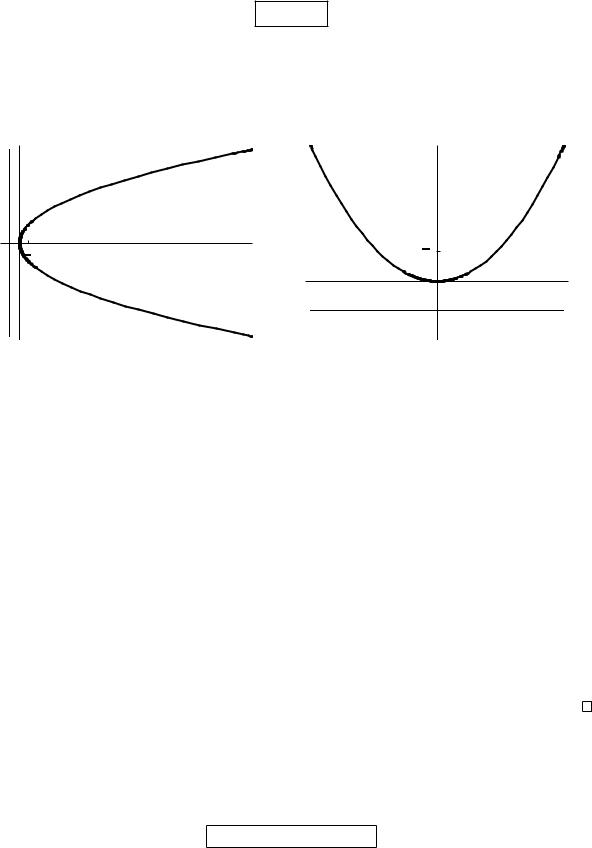
Параболой называют кривую, заданную уравнением |
|
|
||
|
|
y2 = 2px: |
|
|
Само уравнение называют каноническим уравнением параболы. Число p называют |
||||
параметром параболы, а точку (0; 0) вершиной. Точку с координатами (p |
; 0) íà- |
|||
зывают фокусом, а прямую x = ¡p2 |
|
2 |
|
|
директрисой. |
|
|
||
Y |
|
|
Y |
|
p |
|
X |
p |
|
2 |
|
|
2 |
|
|
|
|
X |
|
|
|
|
|
|
|
Рис. 10: Параболы y2 = 2px è 2py = x2 |
|
||
Задача 36. Построить кривую y = ¡2x2 + 6x + 3. Решение. Выделим полный квадрат:
|
y = ¡2x2 + 6x + 3; |
|
|
|
|
|
|
|||||||||||||||
|
y = ¡2(x2 ¡ 3x) + 3; |
|
|
|||||||||||||||||||
y = ¡2³x2 |
|
|
3 |
|
|
|
32 |
32 |
´ + 3; |
|
|
|||||||||||
¡ 2x |
|
|
|
+ |
|
|
¡ |
|
|
|
|
|
|
|||||||||
2 |
|
222 |
22 |
|
|
|||||||||||||||||
|
= ¡2³ |
|
¡ 2 |
2 |
3 |
22 |
´15 |
2 |
|
|
||||||||||||
y |
x2 |
|
x |
3 |
+ |
3 |
+ |
|
9 |
+ 3; |
|
|
||||||||||
|
´ |
|
|
|
||||||||||||||||||
|
15 ³ |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||
|
y = ¡2 x ¡ |
2 |
+ |
|
2 |
; |
|
|
|
|
||||||||||||
|
y ¡ |
|
= ¡2³x ¡ |
|
´: |
|
|
|||||||||||||||
|
2 |
2 |
|
¢. |
||||||||||||||||||
Итак, получилась парабола y = ¡2x2, вершина которой смещена в точку ¡ |
23 ; 152 |
|||||||||||||||||||||
7.11 Уравнение плоскости
Общим уравнением плоскости называют уравнение вида
Ax + By + Cz + D = 0
