Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Финансовый университет при Правительстве РФ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lin_Alg-BE

.pdf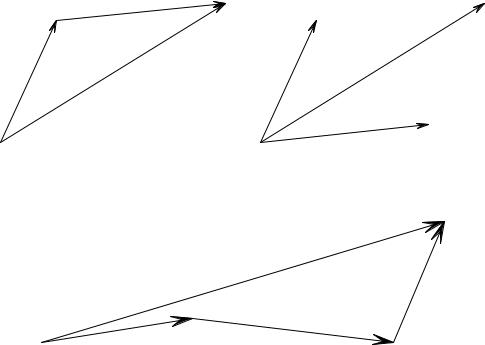

Скачиваний:

Добавлен:

13.03.2015

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

December 6, 2011 Курбатов В.Г.		30
b
a•	a•
• • ••	• •	••
c=a+b	c=a+b

••

Рис. 1: Слева: правило треугольника. Справа: правило параллелограмма.

•• •• •

a+b+c

c•

••

Рис. 2: Правило замкнутой цепочки векторов.

3.2 Числовая проекция вектора

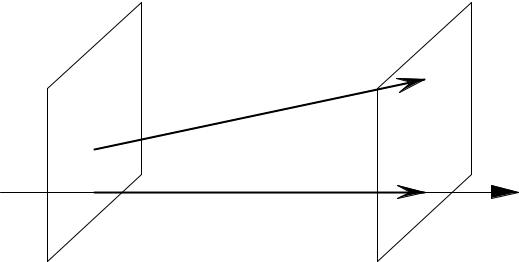
Рассмотрим в пространстве точку A и прямую L. Проведем через точку A плоскость ®, ортогональную прямой L. Точку A1 пересечения ® è L называют проекцией

точки A на прямую L.

¡!

Рассмотрим в пространстве произвольный вектор a¯ = AB. Пусть точки A1 è

¡¡¡!

B1 являются проекциями точек A è B, соответственно. В этом случае вектор A1B1

¡!

называют (векторной) проекцией вектора AB на прямую L и обозначают символом

¡¡¡ïð !

L a¯.

December 6, 2011 Курбатов В.Г.

Рис. 3: Проекция вектора на ось

December 6, 2011

Курбатов В.Г.

Зададим на прямой L направление (и масштаб). Прямую с направлением назы-

âàþò îñüþ.

a¯ =

¡!

L ¯ =

¡!

Числовой проекцией вектора

ïð

AB называют число пр

AB, равное

¡¡¡!

длине проекции

, если направления L è A

совпадают, и равное

, åñ-

¡j 1

ли их направления противоположны. Очевидно, равные векторы имеют одинаковые
числовые проекции.
Теорема 10. Числовые проекции обладают следующими свойствами:
¯	¯

1) ïðL(¯a + b) = ïðL a¯ + ïðL b; 2) ïðL(¸a¯) = ¸ ïðL a¯.

3.3 Декартова система координат

Декартовой1) (прямоугольной) системой координат в пространстве называют систему, состоящую из начальной точки O, трех взаимно ортогональных осей X,

Y è Z, проходящих через точку O, и единичного отрезка, являющегося эталоном измерения. Аналогично определяется декартова система координат на плоскости.

Рис. 4: Нахождение координат точки A в декартовой системе координат.

Координатами вектора a¯ относительно декартовой системы координат называют числовые проекции x, y è z вектора a¯ íà îñè X, Y è Z соответственно. x называют

абсциссой, y ординатой и z аппликатой.

¡!

Рассмотрим в пространстве произвольную точку A (см. рис. 4). Вектор a¯ = OA

называют радиус-вектором точки A. Координатами точки A называют координаты

¡!

радиус-вектора OA.

1)Декарт знаменит, например, своим высказыванием: Я мыслю, значит, я существую .

December 6, 2011 Курбатов В.Г.

Координаты вектора принято записывать через знак равенства, а координаты точки около точки: a¯ = (x; y; z), A(x; y; z).

Теорема 11. Пусть a¯ = (a1; a2; a3)	è ¯	; b2; b3). Тогда
	b = (b1

(a) a¯ + b = (a1 + b1; a2 + b2; a3 + b3);

(b) ¸a¯ = (¸a1; ¸a2; ¸a3).

Доказательство. Вытекает из теоремы 10. Докажем, к примеру (a). Пусть c¯ =

¯	¯	¯	+b1. Аналогично yc = a2			+b2
a¯+b. Имеем xc = ïðX c¯ = ïðX (¯a+b) = ïðX a¯+ïðX b = a1
è zc = a3 + b3.
Замечание 3. Геометрически очевидно, что векторы a¯ = (a1; a2; a3)				è ¯	; b2	; b3)
				b = (b1

параллельны (коллинеарны), если для некоторого ¸ выполняется равенство a¯ = ¸b. Или в координатной форме:

(a1; a2; a3) = (¸b1; ¸b2; ¸b3):

Для существования такого ¸ необходимо и достаточно, чтобы совпали три числа:


	a1	=	a2	=		a3	:
	b1
			b2			b3
Это равенство называют условием параллельности векторов.
Задача 13. Являются ли векторы a¯ = (2; 1; 3)					è ¯
						b = (¡3; 3; 1) параллельными?

Решение. В силу замечания 3 для параллельности векторов должны выполняться
равенства	2	1		3

		=		=		:
	¡3		3		1
Видно, что это не так. Следовательно, векторы a¯						è ¯
						b не являются коллинеарными.

Ортами или базисными векторами, соответствующими данной декартовой систе-
ме координат, называют единичные векторы ¯, ¯ è ¯, имеющие те же направления,
что и оси координат		,		è			i	j		k	, ¯
что и оси координат		,		è		, соответственно. Очевидно, что ¯					, ¯
è ¯	X		Y		Z					i = (1; 0; 0)	j = (0; 1; 0)
è ¯
k = (0; 0; 1).
Теорема 12. Любой вектор a¯ = (x; y; z) можно представить в виде суммы
						¯	¯	¯			(3.1)
						a¯ = xi + yj + zk:
Эту формулу называют разложением вектора										по базисным векторам ¯, ¯, ¯.
									a¯		i j k
Доказательство. Действительно, ¯							¯	¯
						xi + yj + zk = x(1; 0; 0) + y(0; 1; 0) + z(0; 0; 1) =

(x; 0; 0) + (0; y; 0) + (0; 0; z) = (x; y; z) = a¯.

December 6, 2011 Курбатов В.Г.

3.4 Скалярное произведение
Скалярным произведением двух векторов a¯	è ¯
Скалярным произведением двух векторов a¯	b называют число, равное произве-

дению длин векторов на косинус угла между ними. Скалярное произведение векторов
a¯	è ¯	¯		¯
a¯	b обозначают символом a¯ ¢ b èëè ha;¯ bi. Таким образом,
			¯	¯
			ha;¯ bi = ja¯j ¢ jbj cos !:
				¯	¯
Замечание 4. Учитывая, что пр¯b a¯ = ja¯j cos ! è ïða¯ b = jbj cos !, скалярное произ-
ведение можно также определить, используя проекции. А именно,
		¯		¯ ¯	(3.2)
		ha;¯ bi = ja¯j ïða¯ b = jbj ïð¯b a:¯			(3.2)

Перечислим основные свойства скалярного произведения.

¯¯

~ha;¯ bi = hb; a¯i,

¯¯

~ha;¯ b + c¯i = ha;¯ bi + ha;¯ c¯i,

¯¯ ¯

~ha;¯ ¸bi = h¸a;¯ bi = ¸ha;¯ bi.

è¯ ¯

~Если векторы a¯ b ненулевые, то ha;¯ bi = 0 тогда и только тогда, когда векторы

è ¯

a¯ b ортогональны.

è ¯

Напомним, что векторы a¯ b называют ортогональными, если угол между ними равен ¼=2.

3.5Выражение скалярного произведения через координаты

Лемма 13. Для всевозможных скалярных произведений базисных векторов ¯, ¯									è ¯
имеем ¯ ¯ ¯ ¯	¯ ¯	è ¯ ¯ ¯ ¯		¯ ¯				i j	k
имеем ¯ ¯ ¯ ¯	¯ ¯	è ¯ ¯ ¯ ¯		¯ ¯		.
i ¢ i = j ¢ j = k ¢ k = 1			i ¢ j = i ¢ k = j ¢ k = 0					è ¯
Теорема 14. Скалярное произведение двух векторов a¯ = (a1; a2; a3)								è ¯	; b3)
								b = (b1; b2	; b3)
может быть вычислено по формуле

			¯	+ a2b2	+ a3b3:
			ha;¯ bi = a1b1	+ a2b2	+ a3b3:
Задача 14. Найти скалярное произведение векторов a¯ = (1; 2; ¡3)							è ¯
							b = (0; 1; 2).

Решение. В силу теоремы 14 имеем ha;¯ bi = 1 ¢ 0 + 2 ¢ 1 + (¡3) ¢ 2 = 2 ¡ 6 = ¡4.

Следствие 15. Длина вектора a¯ = (a1; a2; a3) может быть вычислена по формуле

ja¯j = a21 + a22 + a23:

Задача 15. Найти длину ja¯j вектора a¯ = (2; ¡2; 1).

Решение. В силу следствия 15 длина ja¯j вектора a¯ = (2; ¡2; 1) равна p4 + 4 + 1 =

p9 = 3.

December 6, 2011 Курбатов В.Г.	35
¯	, ¯
Задача 16. Найти длину вектора 3¯a ¡ 2b, ãäå a¯ = (1; 2; 3)	b = (4; ¡5; 0).

Решение. Сначала найдем координаты вектора 3¯a ¡ 2b:

3¯a ¡ 2b =3 ¢ (1; 2; 3) ¡ 2 ¢ (4; ¡5; 0) = (3; 6; 9) ¡ (8; ¡10; 0) =(3 ¡ 8; 6 + 10; 9 ¡ 0) = (¡5; 16; 9):

Теперь найдем длину этого вектора в соответствии со следствием 15:

j ¡ j

+ a

3¯a 2b = a

+ a3

= p

=a¯p

¼ 19:

(¡5)

+ 16

+ 9

25 + 256 + 81

362

Пусть дан ненулевой вектор a¯. Рассмотрим вектор e¯ =

. Покажем, что он имеет

ja¯j

же направление, что и вектор a¯. Переход¯

a¯

от вектора a¯ к вектору e¯ =

a¯

называют

нормированием вектора a¯.

длину, равную 1. Действительно, je¯j =

jaa¯¯j

= ja¯1jja¯j = 1. Очевидно, вектор e¯ имеет то

Задача 17. Нормируйте вектор a¯ = (5; ¡6; 7).

Решение. Имеем

ja¯j = p

= p

52 + (¡6)2 + 72

25 + 36 + 49

110

Поэтому

ja¯j

p110

³p110

p110

e¯ =

a¯

(5; ¡6; 7)

;

¡6

;

Следствие 16. Расстояние между точками A(a1; a2; a3) è B(b1; b2; b3) может быть вычислено по формуле

jABj = p

(b1 ¡ a1)2 + (b2 ¡ a2)2 + (b3 ¡ a3)2

(3.3)

a¯ =

¡!

¯ = ¡¡!

¡ ¡!

= ( 1 ¡

2 ¡

¡ 3)

Доказательство. Пусть

AB. Тогда a

Отсюда

jABj = ja¯j = p

(b1 ¡ a1)2 +

(b2 ¡ a2)2 + (b3 ¡ a3)2:

Задача 18. Найти длину jABj отрезка AB, ãäå A(1; 0; 3) è B(0; 2; 1).

Решение. В силу формулы (3.3) имеем

jABj = p

(0 ¡ 1)2 + (2,

¡ 0)2 + (1 ¡ 3)2 = 3:

Задача 19. Даны векторы a¯è= (2; ¡1; 3)

b = (4; 0; ¡3). Найти (a) a¯ ¢ b, (b) j3¯a ¡ 2bj,

Ответ: (a)

; (b) p

; (c)

¡1

238

e¯a¯ = (p14 ; p14

; p14 )

e¯b

= (0; 8; 0; ¡0; 6)

December 6, 2011 Курбатов В.Г.

3.6 Угол между двумя векторами

Теорема 17. Косинус

óãëà

между

векторами

a¯ = (a1; a2; a3)

è ¯

b = (b1; b2; b3) может быть найден по формуле

a1b1 + a2b2 + a3b3

cos ! =

ha;¯ bi

(3.4)

, òî èçp

b1 + b2 + b3

ja¯j ¢ jbj

+ a2 + a3

Замечание 5. Если

формулы (3.4) видно, что

. Поэтому

равенство

a¯ ¢ b = 0

cos ! = 0

a1b1 + a2b2 + a3b3 = 0

называют условием перпендикулярности (ортогональности) векторов. Ср. со свой-

ством 4 скалярного произведения.

è ¯

Задача 20. Найти угол между векторами a¯ = (1; 2; 5)

b = (¡1; 3; 0).

Решение. Воспользуемся формулой (3.4). Имеем

cos ! =

¢ (¡1) + 2 ¢ 3 + 5 ¢ 0

p1 + 4 + 25p1 + 9 + 0

p300

2p3

! = arctg

Задача 21. Найти косинус угла ABC треугольника ABC, ãäå A(2; ¡3; 0), B(3; 1; 2),

C(1; ¡2; 4).

Решение. Угол ABC можно интерпретировать как угол между векторами

a¯ =

¡!

3; 0)

(3; 1; 2) = (2

1; 0

2) = (

2);

BA = (2;

b = ¡¡!

BC = (1;

2; 4)

(3; 1; 2) = (1

1; 4

2) = (

3; 2):

Косинус угла между векторами найдем по формуле (3.4):

cos ! =

ha;¯ bi

(¡1) ¢ (¡2) + (¡4) ¢ (¡3) + (¡2) ¢ 2

2 +p

ja¯j ¢ jbj

(

1) + ( 4)

+ (

2) ( 2) + ( 3)

+ 2

p1 + 16 + 4p4 + 9 + 4

p21 ¢ 17

p357

Задача 22. Являются ли векторы a¯ = (2; 1; 3)

è ¯

b = (¡3; 3; 1) перпендикулярными?

Решение. Воспользуемся замечанием 5 и найдем скалярное произведение:

ha;¯ bi = 2 ¢ (¡3) + 1 ¢ 3 + 3 ¢ 1 = ¡6 + 3 + 3 = 0:

Следовательно, векторы a¯

è ¯

b перпендикулярны.

Задача 23. Составить уравнение прямой, проходящей через точку (x0; y0) перпендикулярно вектору (A; B).

Решение. Ответ задается формулой

A(x ¡ x0) + B(y ¡ y0) = 0:

Действительно, это равенство означает перпендикулярность вектора (x ¡ x0; y ¡ y0), лежащего на прямой, вектору (A; B).

Глава 4

Арифметическое векторное пространство

4.1 Основные понятия

Если в трехмерном пространстве фиксированы декартовы координаты, его при- нято обозначать символом R3. Аналогичным образом плоскость называют двумер-

ным пространством и обозначают R2. Одномерное пространство R1 ýòî îñü. Â этом параграфе мы рассмотрим абстрактное n-мерное пространство Rn, обобщающее

R3, R2 è R1.

Упорядоченный набор из n чисел (x1; x2; : : : ; xn) называют n-мерным (арифметическим) вектором, или просто вектором, или точкой и обозначают x¯. Арифме-

тический вектор обычно записываются в виде столбца или строки. Таким образом, арифметический вектор можно представлять себе как матрицу-столбец или матрицустроку. Числа xi, i = 1; 2; : : : ; n, называют компонентами или координатами векто-

ра. Множество всех n-мерных векторов называют n-мерным арифметическим пространством и обозначают Rn.

Следующие определения совпадают с аналогичными определениями для матриц. Векторы x¯ = (x1; x2; : : : ; xn) è y¯ = (y1; y2; : : : ; yn) называют равными, если x1 = y1,

x2 = y2, . . . , xn = yn. Суммой векторов x¯ è y¯ называют вектор x¯ + y¯ = (x1 + y1; x2 +

y2; : : : ; xn + yn). Аналогично определяют разность. Произведением числа ¸ и вектора
x¯ называют вектор ¸x¯ = x¸¯ = (¸x1; ¸x2; : : : ; ¸xn). Ср. с теоремой 11.
Нулевым называют вектор ¯					, имеющий нулевые координаты. Оче-
видны тождества	0	= (0; 0; : : : ; 0)				¯ ¯,	¯.
	¯,	¯	¯	,
	x¯ ¡ x¯ = 0 x¯ + 0 = x¯ ¡ 0 = x¯					¸0 = 0 0 ¢ x¯ = 0

Теорема 18. Операции сложения и умножения на число обладают свойствами:

1. x¯ + y¯ = y¯ + x¯.
2. (¯x + y¯) + z¯ = x¯ + (¯y + z¯).				¯	äëÿ âñåõ				.
3.	Имеется такой вектор ¯, ÷òî			¯	äëÿ âñåõ				.
4.	Для любого		0	x¯ + 0 = x¯			, ÷òî	x¯	¯.
4.	Для любого		существует такой вектор			¡x¯	, ÷òî		¯.
5.	1¯x = x¯.	x¯				¡x¯		x¯ + (¡x¯) = 0
5.	1¯x = x¯.
6.	®(¯x¯) = (®¯)¯x.
7. (® + ¯)¯x = ®x¯ + ¯x¯.
8.	®(¯x + y¯) = ®x¯ + ®y¯.

December 6, 2011 Курбатов В.Г.

Оказывается, подавляющее большинство свойств пространства Rn является след-

ствием только этих 8 свойств. Более того, имеется много других примеров множеств X, на которых определены операции сложения и умножения на число, для которых

эти свойства выполняются. Например, множество всех многочленов или множество всех функций с общей областью определения. Всякое такое множество X называ-

ют векторным (линейным) пространством, а эти 8 свойств аксиомами линейного пространства. Для любого линейного пространства имеет смысл вся дальнейшая теория.

4.2 Линейная независимость

Возьмем в линейном пространстве X систему из k векторов x¯1, x¯2, . . . , x¯k. Всякий

вектор вида

®1x¯1 + ®2x¯2 + ¢ ¢ ¢ + ®kx¯k;

ãäå ®1, ®2,. . . , ®k числа, называют линейной комбинацией векторов x¯1, x¯2, . . . , x¯k. Систему векторов называют линейно зависимой, если можно подобрать числа ®1, ®2,. . . , ®k так, чтобы не все они были равны нулю и при этом выполнялось равенство

¯	(4.1)
®1x¯1 + ®2x¯2 + ¢ ¢ ¢ + ®kx¯k = 0:

Для системы, состоящей из двух геометрических векторов, линейная зависимость означает, что векторы коллинеарны. Для системы, состоящей из трех геометриче- ских векторов, линейная зависимость означает, что векторы лежат в одной или на параллельных плоскостях.

Систему векторов называют линейно независимой, если она не является линейно зависимой, т. е. если равенство (4.1) возможно только при условии, что ®1 = ®2 =

¢ ¢ ¢ = ®k = 0. Эти определения дословно переносятся на матрицы-строки и матрицыстолбцы.

Теорема 19. Система векторов x¯1, x¯2,. . . , x¯k линейно зависима тогда и только тогда,

когда один из векторов системы можно представить в виде линейной комбинации остальных векторов.

Теорема 20. Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов).

Задача 24. Найти (максимальное) число линейно независимых среди следующих век-

торов: (1; 0; 1), (2; 1; 3), (3; ¡1; 2), (4; 2; 6).

Решение. Составим из этих векторов матрицу:

00	1	1	21	:
1	2	3	4
@1	3	¡2	6A

Из примера 14: ранг этой матрицы равен 2. Поэтому в ней два линейно независимых столбца.

x¯ = (x1; x2; : : : ; xn) имеем (ср. с формулой (3.1))

December 6, 2011 Курбатов В.Г.

4.3 Размерность и базис

Максимальное число линейно независимых векторов, которое можно образовать из элементов линейного пространства X, называют размерностью этого простран-

ства и обозначают символом dim X. Иными словами, число n является размерностью пространства X, если в нем имеется n линейно независимых векторов, но любые n+1

вектор образуют линейно зависимую систему.

Базисом в линейном пространстве X размерности n называют любую систему e¯1, e¯2, : : : , e¯n èç n линейно независимых векторов.

Теорема 21. Пусть e¯1, e¯2, : : : , e¯n базис линейного пространства X. Тогда всякий вектор x линейного пространства X можно единственным образом представить в

âèäå	x¯ = ®1e¯1	+ ®2e¯2 + ¢ ¢ ¢ + ®ne¯n;	(4.2)

т. е. в виде линейной комбинации векторов e¯1, e¯2, : : : , e¯n.

Формулу (4.2) называют разложением вектора x¯ по базису e¯1, e¯2, : : : , e¯n, а числа ®1, ®2, . . . , ®n координатами вектора x¯ в этом базисе. Ср. с формулой (3.1).

Пример 25. Убедимся, что векторы

e¯1 = (1; 0; 0; : : : ; 0); e¯2 = (0; 1; 0; : : : ; 0);

: : : : : : : : : : : : : : : : : :

e¯n = (0; 0; 0; : : : ; 1)

образуют базис. Этот базис в Rn называют стандартным или каноническим. Действительно, для любого вектора

x¯ = x1e¯1 + x2e¯2 + ¢ ¢ ¢ + xne¯n:

Рассмотрим систему из n векторов

e¯i = (e1i; e2i; : : : ; eni);

i = 1; 2; : : : ; n:

Составим матрицу из их координат:

e11

BBe21

B @ . en1

e12 e22

en.2

: : : e1n

: : : e2nCC:

... . C

: : : enn

Такую матрицу называют матрицей системы векторов, а ее определитель определителем системы векторов.

Теорема 22. Для того чтобы система из n векторов являлась базисом, необходимо и достаточно, чтобы определитель этой системы был отличен от нуля.

Доказательство. Доказательство вытекает из теоремы 20.

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.03.2015318.02 Кб37linalgebra.pdf
#
13.03.201596.2 Кб183LindaHoku.МПУР.С оглавлением.docx
#
13.03.2015561.15 Кб39lineynaya_algebra.pdf
#
25.09.20194.41 Mб15Lingvisticheskoe_obespechenie.docx
#
13.03.2015328.1 Кб34Linux part 2.pdf
#
13.03.20151.01 Mб17Lin_Alg-BE.pdf
#
13.03.201557.34 Кб18Logicheskie_zadania.doc
#
13.03.201547.31 Кб133Logika_-_kontrolnaya_TsVET (1).docx
#
21.11.20192.16 Mб4LR10-ITN-22-fevralya-2011-Got.doc
#
21.07.20191.2 Mб5Lvs Mitrohov S.docx
#
13.03.2015635.79 Кб26Lyubimtseva_S_N__Koreneva_V_N_L_93_Kurs_angli.PDF