
Lin_Alg-BE
.pdf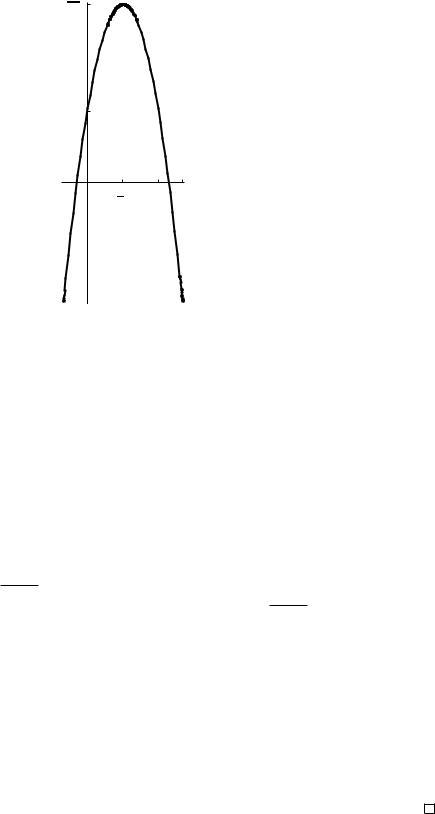
December 6, 2011 Курбатов В.Г. |
60 |
15Y |
|
|
|
2 |
|
|
|
3 |
|
|
|
3 |
|
X |
|
3 |
4 |
||
2 |
|||
|
|
Рис. 11: Парабола из задачи 36
в предположении, что хотя бы один из коэффициентов A, B èëè C отличен от нуля. Покажем, что вектор n¯ = (A; B; C) является перпендикулярным плоскости. Вектор n¯ = (A; B; C) называют нормальным от слова нормаль вектором плоскости.
Пусть точка M0(x0; y0; z0) принадлежит плоскости, т. е.
Ax0 + By0 + Cz0 + D = 0:
Вычитая предыдущие равенства друг из друга, приходим к уравнению
A(x ¡ x0) + B(y ¡ y0) + C(z ¡ z0) = 0; |
(7.3) |
которое можно интерпретировать как равенство нулю скалярного произведения векторов n¯ = (A; B; C) è M0M = (x ¡ x0; y ¡ y0; z ¡ z0). Таким образом, уравнению
удовлетворяют в точности те точки M, для которых вектор M0M перпендикулярен вектору n¯.
Задача 37. Составить уравнение плоскости, проходящей через точку (5; 7; ¡3) перпендикулярно вектору (4; ¡6; 8).
Решение. Уравнение (7.3) является решением задачи: составить уравнение плоскости, проходящей через точку (x0; y0; z0) перпендикулярно вектору (A; B; C). Îñòà-
ется подставить наши данные:
4(x ¡ 5) ¡ 6(y ¡ 7) + 8(z + 3) = 0:
Далее можно раскрыть скобки и привести подобные.
Если хотя бы один из коэффициентов A, B èëè C равен нулю, то уравнение плоскости называют неполным. Например, если C = 0, то вектор n¯ = (A; B; 0) параллелен плоскости XY , и значит, сама прямая параллельна оси Z.
December 6, 2011 Курбатов В.Г. |
61 |
n |
M |
|
|
|
M0 |
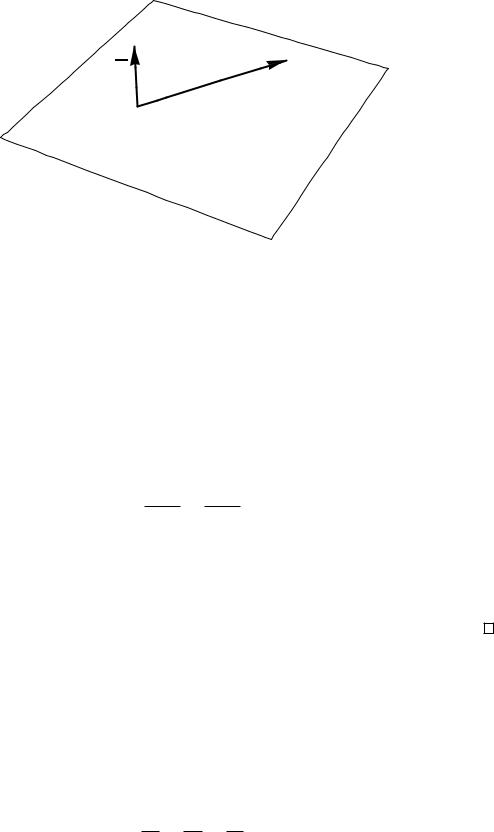
Рис. 12: Геометрический смысл вектора n¯ = (A; B; C)
Задача 38. Составить уравнение плоскости, проходящей через точки M(1; 2; 3) è N(0; 1; 5) параллельно оси Z.
Решение. Параллельность плоскости оси Z означает, что ее уравнение имеет вид
Ax + By + D = 0.
В плоскости XY составим уравнение прямой, проходящей через точки M1(1; 2) è N1(0; 1). Воспользуемся задачей 30:
y ¡ 2 |
= |
x ¡ 1 |
1 ¡ 2 |
0 ¡ 1 |
|
Èëè
y ¡ 2 = x ¡ 1:
Èëè
y ¡ x = 1:
Проверка: эта плоскость проходит через нужные точки и параллельна оси Z.
Из перпендикулярности вектора n¯ = (A; B; C) плоскости следует, что две плоско-
ñòè
A1x + B1y + C1z + D1 = 0; A2x + B2y + C2z + D2 = 0
параллельны (перпендикулярны) тогда и только тогда, когда их нормальные векторы n¯1 = (A1; B1; C1) è n¯2 = (A2; B2; C2) параллельны (перпендикулярны). Отсюда
получаем условие параллельности
A1 = B1 = C1 A2 B2 C2

December 6, 2011 Курбатов В.Г. |
62 |
и условие перпендикулярности
A1 ¢ A2 + B1 ¢ B2 + C1 ¢ C2 = 0
двух плоскостей.
7.12 Уравнение прямой
Прямую в пространстве можно задать как пересечение двух плоскостей, т. е. как множество решений системы уравнений
½A1x + B1y + C1z + D1 = 0; A2x + B2y + C2z + D2 = 0:
Эти две плоскости определены неоднозначно. Разумно выбирать их возможно более простыми. Считается, что самый простой вид это
|
x ¡ x1 |
= |
y ¡ y1 |
= |
z ¡ z1 |
: |
(7.4) |
|
l |
m |
n |
||||
|
|
|
|
|
Здесь два уравнения. Например, уравнение
x ¡ x1 = y ¡ y1 l m
задает плоскость, параллельную оси Z.
Уравнения (7.4) называют каноническими уравнениями прямой.
Очевидно, точка (x1; y1; z1) лежит на прямой. Вектор q¯ = (l; m; n) параллелен прямой. Его называют направляющим вектором прямой.
Задача 39. Составить уравнение прямой, проходящей через точку (5; 7; ¡3) параллельно вектору (4; ¡6; 8).
Решение. Уравнение (7.4) является решением задачи: составить уравнение прямой, проходящей через точку (x1; y1; z1) параллельно вектору (l; m; n). Остается под-
ставить наши данные: |
|
x ¡ 5 |
|
y ¡ 7 |
|
z + 3 |
|
|
|
= |
= |
: |
|||
|
4 |
|
|
||||
|
¡6 |
8 |
|
||||
Углы между плоскостями и прямыми это по определению углы между их нормальными и направляющими векторами. Их находят с помощью теоремы 17. В частности, имеем условие параллельности
l1 = m1 = n1 l2 m2 n2
и условие перпендикулярности
l1 ¢ l2 + m1 ¢ m2 + n1 ¢ n2 = 0
двух прямых.
